Hans Walser, [20220705]

arctan und pythagoreische Dreiecke

1 Worum geht es?

Winkelbeziehungen im Kontext von pythagoreischen Dreiecken. Beweise ohne Worte.

2 Beweis ohne Worte

Es gilt:

Die Abbildung 1 zeigt einen Beweis ohne Worte.

Abb. 1: Beweis ohne Worte

3 Pythagoreische Dreiecke

Das gelbe Dreieck (Abb. 1) hat das Seitenverhältnis 3:4:5. Es ist das sogenannte „Lehrerdreieck“, das einfachste pythagoreische Dreieck (ägyptisches Dreieck).

Wir können analog mit anderen pythagoreischen Dreiecke fuhrwerken. Die Abbildung 2 zeigt das pythagoreische Dreieck mit dem Seitenverhältnis 5:12:13 (indisches Dreieck).

Abb. 2: Indisches Dreieck

Die zugehörigen Winkelbeziehungen sind:

4 Allgemein

Zur Konstruktion eines pythagoreischen Dreiecks wählen wir die beiden Parameter u und v mit folgenden Bedingungen: u > v, u, v teilerfremd und u – v ungerade. Dann sind

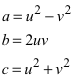
die Seiten eines pythagoreischen Dreiecks.

Im Beispiel der Abbildung 1 ist u = 2 und v = 1. Im Beispiel der Abbildung 2 ist u = 3 und v = 2.

Es gilt allgemein folgende Winkelbeziehung:

Beweis: Wir formen die obere der beiden Winkelbeziehungen um:

Aus dem Additionstheorem für den Tangens ergibt sich:

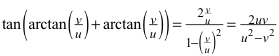
Damit ist die obere Winkelbeziehung bewiesen. Die untere Winkelbeziehung kann analog bewiesen werden. Beim Beweisvorgang werden die einschränkenden Bedingungen über die Parameter u und v nicht verwendet. Die Winkelbeziehungen gelten also auch ohne diese Einschränkungen.

5 Technisches

Beim Beweis ohne Worte wird das Rasterrechteck immer größer und unübersichtlich. Die Abbildung 3 zeigt die Situation für u = 4 und v = 1.

Abb. 3: Rasterrechteck

Das Rasterrechteck hat allgemein die Dimensionen gemäß Abbildung 4.

Abb. 4: Dimensionen

6 Sonderfall mit Goldenem Schnitt

Im Sonderfall der Abbildung 1 ist der größere der beiden spitzen Winkel des roten Dreiecks:

Dieser Winkel ist auch der spitze Winkel im goldenen Rhombus (Abb. 5). Das ist der Rhombus, dessen Diagonalen im Verhältnis des Goldenen Schnittes stehen. Es ist auch der Seitenrhombus im Rhombentriakontaeder (Abb. 6).

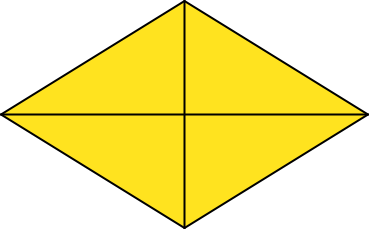
Abb. 5: Goldener Rhombus

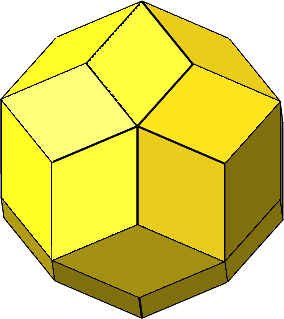
Ein Bild, das gelb enthält.

Automatisch generierte Beschreibung

Abb. 6: Rhombentriakontaeder

Die Winkeleigenschaft bedeutet, dass wir vier goldene Rhomben und zwei pythagoreische Dreiecke mit dem Seitenverhältnis 3:4:5 um einen Punkt herum gruppieren können. Die Abbildung 7 zeigt einige Lösungen.

Abb. 7.1: Rosette

Abb. 7.2: Rosette

Abb. 7.3: Rosette

Abb. 7.4: Rosette

Literatur

Alsina, Claudi & Nelsen, Roger B. (2013): Bezaubernde Beweise: eine Reise durch die Eleganz der Mathematik. Berlin: Springer Spektrum.

Nelsen, Roger B. (2000): Proofs without Words. MAA, The Mathematical Association of America. ISBN 978-0883857007

Walser, Hans (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wußing über populärwissenschaftliche Mathematikliteratur aus Leipzig. Edition am Gutenbergplatz, Leipzig. ISBN 978-3-937219-85-1.

Weblinks

Hans Walser: Tetraeder in Halbkugel

http://www.walser-h-m.ch/hans/Miniaturen/T/Tetraeder_in_Halbkugel/Tetraeder_in_Halbkugel.html

Hans Walser: arctan

http://www.walser-h-m.ch/hans/Miniaturen/A/arctan/arctan.html

Hans Walser: Pythagorean Triangles

http://www.walser-h-m.ch/hans/Miniaturen/P/Pythagorean_Triangles/Pythagorean_Triangles.htm