Hans Walser, [20081117a]
Das Basler Problem
Anregung: P. B., L. und M. G., S. G.
1 Worum es geht
Jacob Bernoulli stellte die Frage um den Grenzwert von [Downey / Ong / Sellers]:
Bernoulli konnte die Frage nicht lšsen. Sie wurde in der Folge als Basler Problem bezeichnet. Erst Euler bewies 1737:
Euler selbst lieferte mehrere Beweise dazu.
Die numerische Berechnung (Excel) zeigt eine recht langsame Konvergenz:
|
k |
1/k^2 |
Summe |
6*Summe |
Wurzel |
|
1 |
1.00000000 |
1.00000000 |
6.00000000 |
2.44948974 |
|
2 |
0.25000000 |
1.25000000 |
7.50000000 |
2.73861279 |
|
3 |
0.11111111 |
1.36111111 |
8.16666667 |
2.85773803 |
|
4 |
0.06250000 |
1.42361111 |
8.54166667 |
2.92261299 |
|
5 |
0.04000000 |
1.46361111 |
8.78166667 |
2.96338770 |
|
6 |
0.02777778 |
1.49138889 |
8.94833333 |
2.99137649 |
|
7 |
0.02040816 |
1.51179705 |
9.07078231 |
3.01177395 |
|
8 |
0.01562500 |
1.52742205 |
9.16453231 |
3.02729786 |
|
9 |
0.01234568 |
1.53976773 |
9.23860639 |
3.03950759 |
|
10 |
0.01000000 |
1.54976773 |
9.29860639 |
3.04936164 |
Es werden folgende Variationen hergeleitet:
2 Der klassische Beweis
Die
Funktion 
hat die
Taylor-Entwicklung
und die
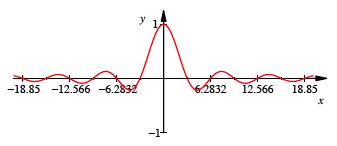
Nullstellen 
. Die Abbildung zeigt den Funktionsgrafen.
Wir bauen nun ein ăNullstellenpolynomŇ mit den passenden Linearfaktoren:
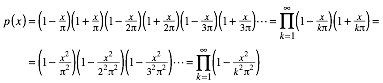
Das
Absolutglied in 
ist 1. Der
Koeffizient von 
ist:
Vergleich
mit dem entsprechenden Koeffizienten von 
liefert:
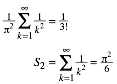
Die
folgende Abbildung zeigt rot die Funktion 
, grźn das Taylorpolynom 
und blau das endliche
Produkt 
. Wir sehen, dass die Funktionsgrafen drastisch verschieden
sind.
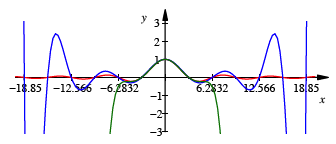
Vergleich der Funktionsgrafen
3 Variante mit Kosinus
3.1 Koeffizient zweiten Grades
Die Kosinusfunktion hat die Taylor-Entwicklung
und die
Nullstellen 
. Daraus ergibt sich das Nullstellenpolynom:
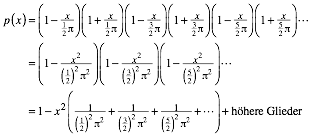
Koeffizientenvergleich mit der Taylor-Entwicklung liefert:
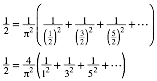
Somit erhalten wir fźr die Reihe der Quadrate der Kehrwerte der ungeraden Zahlen:
Die Konvergenz ist auch nicht umwerfend, aber doch besser als auf dem klassischen Weg:
|
k |
2*k-1 |
1/(2*k-1)^2 |
Summe |
8*Summe |
Wurzel |
|
1 |
1 |
1.00000000 |
1.00000000 |
8.00000000 |
2.82842712 |
|
2 |
3 |
0.11111111 |
1.11111111 |
8.88888889 |
2.98142397 |
|
3 |
5 |
0.04000000 |
1.15111111 |
9.20888889 |
3.03461511 |
|
4 |
7 |
0.02040816 |
1.17151927 |
9.37215420 |
3.06139743 |
|
5 |
9 |
0.01234568 |
1.18386495 |
9.47091963 |
3.07748593 |
|
6 |
11 |
0.00826446 |
1.19212942 |
9.53703533 |
3.08820908 |
|
7 |
13 |
0.00591716 |
1.19804658 |
9.58437261 |
3.09586379 |
|
8 |
15 |
0.00444444 |
1.20249102 |
9.61992816 |
3.10160090 |
|
9 |
17 |
0.00346021 |
1.20595123 |
9.64760982 |
3.10606018 |
|
10 |
19 |
0.00277008 |
1.20872131 |
9.66977049 |
3.10962546 |
Nun gelten bei den Numerologen (Zahlenmystikern) die ungeraden Zahlen als mŠnnlich, die BeschrŠnkung auf die ungeraden Zahlen ist also sexistisch. TatsŠchlich ergibt sich aber aus dieser Formel die klassische Formel. Dies kann wie folgt gezeigt werden. Aus
erhalten wir durch Trennung in gerade und ungerade Anteile:
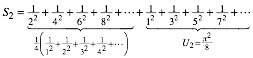
Somit ist:
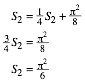
3.2 Koeffizient vierten Grades
Aus dem Nullstellenpolynom
lesen wir
mit einigen kombinatorischen †berlegungen den Koeffizienten 
fźr 
ab. Dazu brauchen
bis auf den gemeinsamen Faktor 
die Summe aller
Produkte von zwei verschiedenen
Faktoren aus der Menge 
. Wir verwenden die folgende †bersicht.
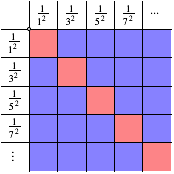
Tabelle
Die roten Felder benštigen wir nicht (zwei gleiche Faktoren), die benštigten blauen Felder kommen je doppelt vor.
Wir
kšnnen aber auch einfach źber die Formel 
nachdenken. Diese
kann umgeschrieben werden zu 
.
Jedenfalls ergibt sich:
Darin
erscheint die schon bekannte Formel 
. Somit ist:
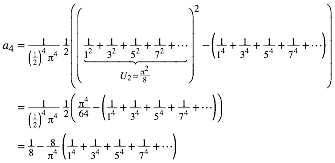
Der Koeffizientenvergleich mit der Taylor-Entwicklung liefert:
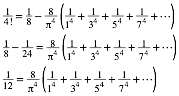
Daraus erhalten wir:
Numerisch sieht das so aus:
|
k |
2*k-1 |
1/(2*k-1)^4 |
Summe |
96*Summe |
Vierte
Wurzel |
|
1 |
1 |
1.00000000 |
1.00000000 |
96.00000000 |
3.13016916 |
|
2 |
3 |
0.01234568 |
1.01234568 |
97.18518519 |
3.13978577 |
|
3 |
5 |
0.00160000 |
1.01394568 |
97.33878519 |
3.14102563 |
|
4 |
7 |
0.00041649 |
1.01436217 |
97.37876853 |
3.14134814 |
|
5 |
9 |
0.00015242 |
1.01451459 |
97.39340044 |
3.14146613 |
|
6 |
11 |
0.00006830 |
1.01458289 |
97.39995737 |
3.14151901 |
|
7 |
13 |
0.00003501 |
1.01461790 |
97.40331860 |
3.14154611 |
|
8 |
15 |
0.00001975 |
1.01463766 |
97.40521489 |
3.14156140 |
|
9 |
17 |
0.00001197 |
1.01464963 |
97.40636431 |
3.14157067 |
|
10 |
19 |
0.00000767 |
1.01465730 |
97.40710095 |
3.14157661 |
Wow, ist das aber gut.
Natźrlich ist die Formel wieder sexistisch. Wir kšnnen aber eine harmlose Formel herleiten.
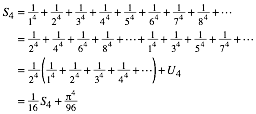
Damit wird:
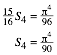
Also:
Natźrlich kann diese Formel auch źber den klassischen Weg hergeleitet werden.
Die
Konvergenz ist etwas weniger gut als bei 
:
|
k |
1/k^4 |
Summe |
90*Summe |
Vierte
Wurzel |
|
1 |
1.00000000 |
1.00000000 |
90.00000000 |
3.08007029 |
|
2 |
0.06250000 |
1.06250000 |
95.62500000 |
3.12710787 |
|
3 |
0.01234568 |
1.07484568 |
96.73611111 |
3.13615238 |
|
4 |
0.00390625 |
1.07875193 |
97.08767361 |
3.13899789 |
|
5 |
0.00160000 |
1.08035193 |
97.23167361 |
3.14016118 |
|
6 |
0.00077160 |
1.08112353 |
97.30111806 |
3.14072172 |
|
7 |
0.00041649 |
1.08154003 |
97.33860244 |
3.14102416 |
|
8 |
0.00024414 |
1.08178417 |
97.36057509 |
3.14120140 |
|
9 |
0.00015242 |
1.08193658 |
97.37429251 |
3.14131204 |
|
10 |
0.00010000 |
1.08203658 |
97.38329251 |
3.14138462 |
3.3 Koeffizient sechsten Grades
Aus dem Nullstellenpolynom
lesen wir
mit einigen kombinatorischen †berlegungen folgenden Koeffizienten 
fźr 
ab. Wir benštigen
die Summe der Produkte von je drei verschiedenen Faktoren aus der Menge 
. Dazu kann entweder eine dreidimensionale Tabelle verwendet
werden oder folgende †berlegung: Aus
ergibt sich:
Jedenfalls erhalten wir:
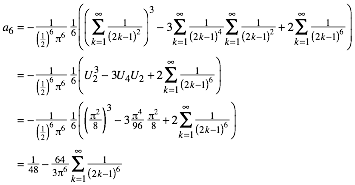
Vergleich
mit den entsprechenden Koeffizienten 
der
Taylor-Entwicklung liefert:
Numerisch erhalten wir eine recht gute Konvergenz.
|
k |
2*k-1 |
1/(2*k-1)^6 |
Summe |
960*Summe |
Sechste
Wurzel |
|
1 |
1 |
1.0000000000 |
1.0000000000 |
960.0000000000 |
3.1408356050 |
|
2 |
3 |
0.0013717421 |
1.0013717421 |
961.3168724280 |
3.1415532643 |
|
3 |
5 |
0.0000640000 |
1.0014357421 |
961.3783124280 |
3.1415867274 |
|
4 |
7 |
0.0000084999 |
1.0014442420 |
961.3864722933 |
3.1415911715 |
|
5 |
9 |
0.0000018817 |
1.0014461236 |
961.3882787027 |
3.1415921553 |
|
6 |
11 |
0.0000005645 |
1.0014466881 |
961.3888205977 |
3.1415924505 |
|
7 |
13 |
0.0000002072 |
1.0014468953 |
961.3890194868 |
3.1415925588 |
|
8 |
15 |
0.0000000878 |
1.0014469831 |
961.3891037667 |
3.1415926047 |
|
9 |
17 |
0.0000000414 |
1.0014470245 |
961.3891435387 |
3.1415926263 |
|
10 |
19 |
0.0000000213 |
1.0014470458 |
961.3891639443 |
3.1415926375 |
3.4 Koeffizient achten Grades
Fźr den
Koeffizienten 
von 
benštigen wir die
Summe der Produkte von je vier verschiedenen Faktoren aus der Menge 
. Dazu brŠuchten wir eine vierdimensionale Tabelle. Helfen
tut auch folgende †berlegung: Aus dem Ansatz
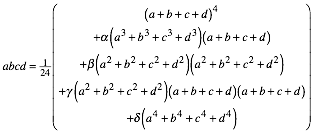
liefern
die Koeffizientenvergleiche fźr 
, 
, 
und 
die Gleichungen
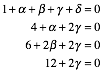
mit der
Lšsung 
. Somit ist:
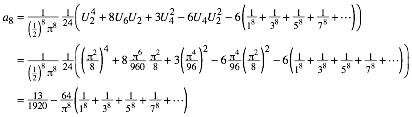
Vergleich
mit dem entsprechenden Koeffizienten 
der
Taylor-Entwicklung ergibt:
Somit:
Numerisch:
|
k |
2*k-1 |
1/(2*k-1)^8 |
Summe |
161280/17*Summe |
Achte
Wurzel |
|
1 |
1 |
1.0000000000 |
1.0000000000 |
9487.0588235294 |
3.1415317202 |
|
2 |
3 |
0.0001524158 |
1.0001524158 |
9488.5048010974 |
3.1415915686 |
|
3 |
5 |
0.0000025600 |
1.0001549758 |
9488.5290879680 |
3.1415925738 |
|
4 |
7 |
0.0000001735 |
1.0001551493 |
9488.5307336551 |
3.1415926419 |
|
5 |
9 |
0.0000000232 |
1.0001551725 |
9488.5309540449 |
3.1415926510 |
|
6 |
11 |
0.0000000047 |
1.0001551772 |
9488.5309983028 |
3.1415926529 |
|
7 |
13 |
0.0000000012 |
1.0001551784 |
9488.5310099329 |
3.1415926533 |
|
8 |
15 |
0.0000000004 |
1.0001551788 |
9488.5310136346 |
3.1415926535 |
|
9 |
17 |
0.0000000001 |
1.0001551789 |
9488.5310149946 |
3.1415926535 |
|
10 |
19 |
0.0000000001 |
1.0001551790 |
9488.5310155532 |
3.1415926536 |
Bei hšheren Potenzen wird die Konvergenz immer besser.
Literatur
[Downey
/ Ong / Sellers] Downey, Lawrence / Ong, Boon W. / Sellers, James A. : Beyond the Basel
Problem: Sums of Reciprocals of Figurate Numbers. The College Mathematics
Journal. Vol. 39, No. 5, November 2008. P. 391-394