Hans Walser, [20080204a]
Kreisfiguren mit berŸhrenden Kreisen
1
Worum es geht
Zu 
werden 
gleich gro§e
Kreise gezeichnet, von denen jeder n andere
Kreise berŸhrt.
2
Beispiele
2.1
n = 1
2.2
n = 2
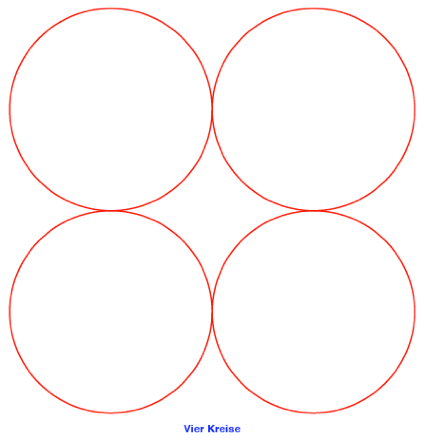
2.3
n = 3
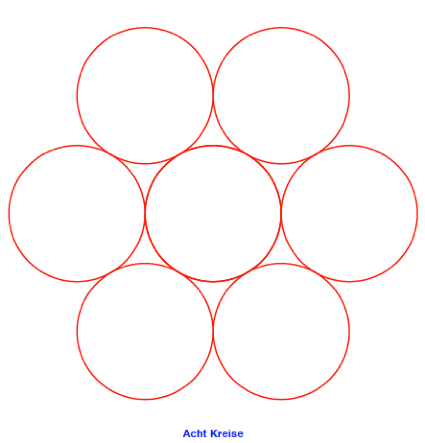
Eigentlich sehen wir
nur sieben Kreise, von denen einer, der zentrale Kreis, von den sechs anderen
Kreisen berŸhrt wird. Wir mŸssen diesen Kreis doppelt zŠhlen und jeden von den
beiden alternierend durch je drei Kreise berŸhren lassen. Wie es zu dieser eigenartigen
ZŠhlweise kommt, wird spŠter erklŠrt.
2.4
n = 4
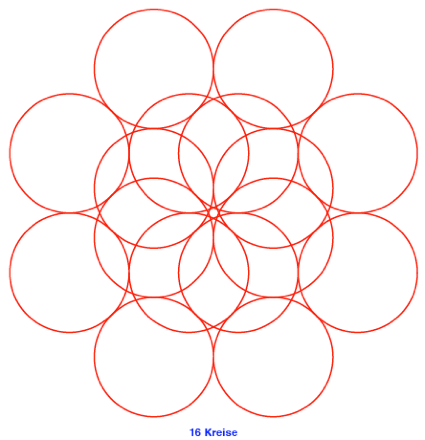
2.5
n = 5
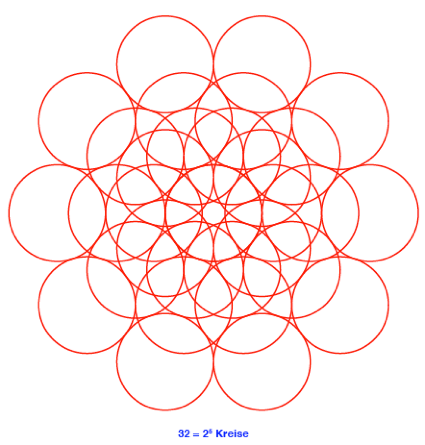
2.6
n = 6
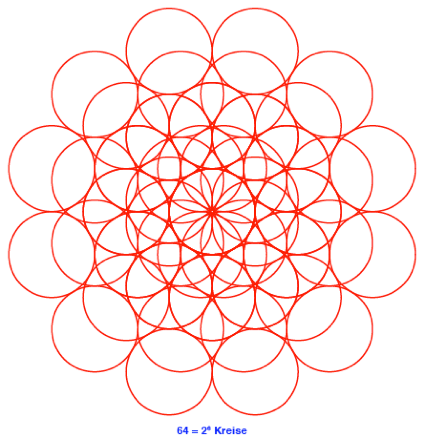
2.7
n = 7
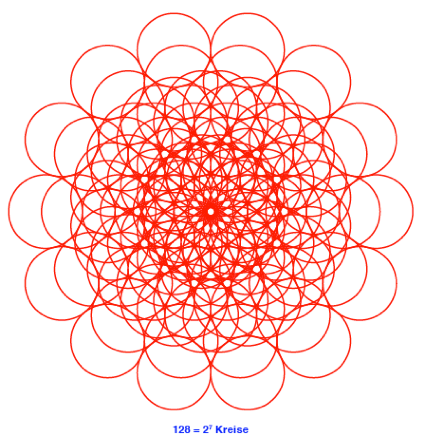
2.8
n = 8
3
Hintergrund
Wir zeichnen einen n-dimensionalen HyperwŸrfel in isometrischer
Darstellung. Von jeder Ecke aus verlaufen kann n gleich stark verkŸrzte Kanten. Daher kann jeder Ecke
als Zentrum eines Kreises verstanden werden, dessen Radius die HŠlfte der LŠnde
der verkŸrzten Kante ist und der daher n Nachbarkreise berŸhrt.
Dies im ebenen Bild. Im
n-dimensionalen Raum entsprechen den
Kreisen Hyperkugeln.
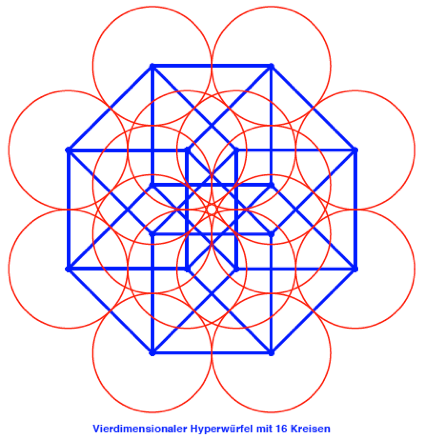
Das folgende Bild illustriert
den Fall 
.
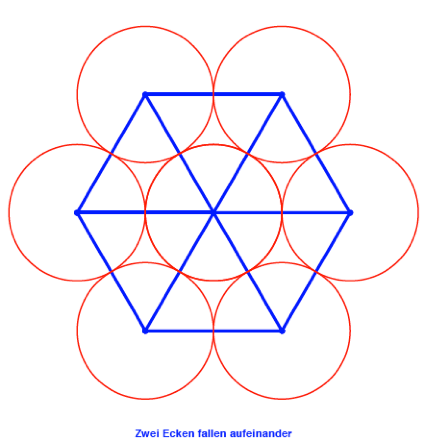
Bei 
fallen in der
isometrischen Darstellung zwei WŸrfelecken aufeinander. Daher die DoppelzŠhlung
des ãzentralenÒ Kreises.
Dieser Effekt tritt
auch bei anderen Dimensionen auf.
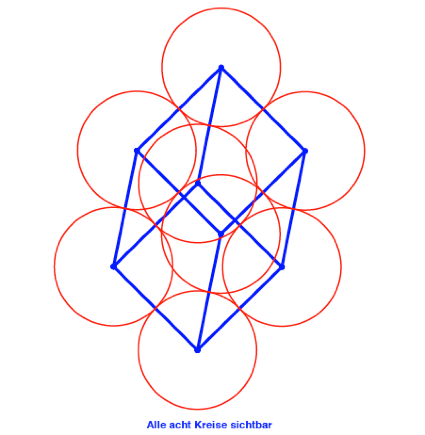
Wenn wir die
WŸrfelecken weniger symmetrisch zeichnen, werden alle acht Kreise sichtbar. In
dieser Situation sind die Winkel zwischen den projizierten Kanten nicht mehr
regelmŠ§ig.
4
MuPAD-Programm
Exemplarisch das
Programm fŸr 
:
n:=4:
N:=2^n-1:
for k from 0 to N do
x[k]:=0:
y[k]:=0:
for j from 1 to n do
x[k]:=x[k]+round(frac(k*(1/2)^(n-j+1)))*cos(j*PI/n):
y[k]:=y[k]+round(frac(k*(1/2)^(n-j+1)))*sin(j*PI/n):
end_for:
end_for:
Kreis:=k->plot::Curve2d([x[k]+1/2*cos(t), y[k]+1/2*sin(t)],
t=0..2*PI, LineWidth=1/2, LineColor=[1,0,0]):
plot(Kreis(k)$k=0..N, Scaling=Constrained, Axes=None,
Width=150, Height=150):