Hans Walser, [20140304], [20160125]

Ein Bild von Max Bill

1     Nachzeichnung des Bildes

Die Abbildung 1 zeigt die Nachzeichnung eines Bildes von Max Bill.

Abb. 1: Nachzeichnung

2     Das Lehrerdreieck

Das einfachste pythagoreische Dreieck hat die SeitenverhŠltnisse 3:4:5. Es kommt in ungezŠhlten Schulaufgaben, Workshops, ArbeitsblŠttern vor und wird daher auch als ãLehrerdreieckÒ bezeichnet.

Auch Max Bill hat etliche Werke auf Grund dieses Dreiecks gestaltet.

Wir nehmen daher einmal an, die drei rechtwinkligen Dreiecke in der Abbildung 1 seien auch von dieser Form und untersuchen, ob das so ãpasstÒ.

Die Abbildung 2 zeigt eine GeoGebra-Zeichnung.

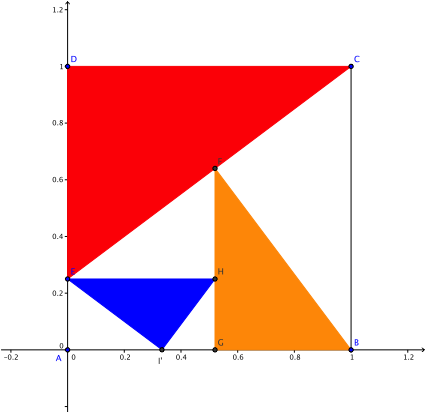
Abb. 2: Figur im Einheitsquadrat

Die Tabelle 1 zeigt die Koordinaten der Punkte der Abbildung 2.

Tab. 1: Koordinaten

Wir sehen, dass der Punkt , also der Eckpunkt am rechten Winkel des blauen Dreieckes, nicht auf der Basislinie des Quadrates sitzt. Der Fehler betrŠgt allerdings nur 0.4 Promille der Quadratseite.

Die drei Dreiecke passen also nicht ins Quadrat.

3     Verbesserung

Wenn wir den Punkt E geringfŸgig tiefer setzen, kommt der Punkt  der Basislinie des Quadrates nŠher (Tab. 2). Die Frage ist natŸrlich, ob das immer noch pythagoreische Dreiecke ergibt.

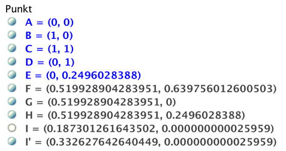
Tab. 2: Verbesserung

4     Parametrisierung

Wir fŸhren als Parameter t die KathetenlŠnge DE ein. Dieser Parameter t ist das KathetenverhŠltnis der rechtwinkligen Dreiecke. FŸr das Lehrerdreieck ist t = 0.75.

Mit einiger Rechnung ergibt sich fŸr die y-Koordinate des Punktes :

 

                                                                                                         (1)

 

Die Bedingung  fŸhrt auf die Gleichung fŸnften Grades:

 

                                                                                                   (2)

 

Wir erhalten die numerische Lšsung t = 0.7503971612. Die oben fŸr den Punkt E gewŠhlte verbesserte y-Koordinate ergibt sich aus 1 – t.

5     Eine Kurve

Wir variieren den Punt E auf der linken Quadratseite. Dann beschreibt der Punkt  die blaue Kurve der Abbildung 3.

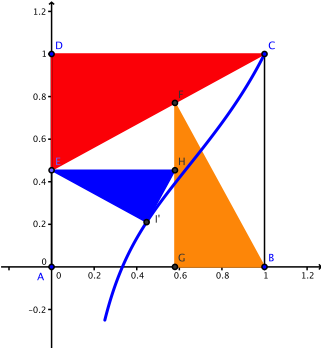
Abb. 3: Ortslinie der Dreiecksecke

6     Fast Šhnliche pythagoreische Dreiecke.

Es gibt pythagoreische Dreiecke, welche fast dieselbe Form wie das Lehrerdreieck haben. So hat etwa das pythagoreische Dreieck mit

 

                                       (3)

 

ein KathetenverhŠltnis

 

                                                                                                           (4)

 

und daher fast die gleiche Form wie das Lehrerdreieck.

Hintergrund: Das Lehrerdreieck ergibt sich aus den Parametern u = 2 und v = 1 durch.

 

                                       (5)

 

Wir wŠhlen nun u und v in einem etwa gleichen VerhŠltnis. Obiges Beispiel wurde mit u = 20000  und v = 9999 generiert.

Es ist daher zunŠchst nicht auszuschlie§en, dass es doch ein pythagoreisches Dreieck gibt, das exakt in die Bildidee von Bill passt.

7     Ausschluss von pythagoreischen Dreiecken

Nach einer Idee von Renato Pandi kann man das aber ausschlie§en wie folgt.

Die Bedingung (2) kšnnen wir umformen zu:

                                                                                         (6)

Nun sei  mit  eine rationale Lšsung. Der Bruch  sei vollstŠndig gekŸrzt, das  hei§t, p und q sind nicht beide gerade.

Wir setzen nun  in (6) ein und erhalten:

 

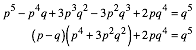                                                                         (7)

 

Nun fŸhren wir mit (7) eine Fallunterscheidung gemŠ§ der ParitŠt von p und q durch:

(I)            p, q beide ungerade

(II)          p gerade, q ungerade

(III)        p ungerade, q gerade

Es wird:

(I)            gerade mal gerade plus gerade = ungerade (falsch)

(II)          ungerade mal gerade plus gerade = ungerade (falsch)

(III)        ungerade mal ungerade plus gerade = gerade (falsch)

Somit sind die pythagoreischen Dreiecke ausgeschlossen.