Hans Walser, [20220725]
Bilinski
1 Worum geht es?
Nicht-konvexe Variante des Bilinski-Rhombendoekaeders.
2 Erinnerung: das übliche Rhombendodekaeder
Die Abbildungen 1 und 2 zeigen das übliche Rhombendodekaeder.
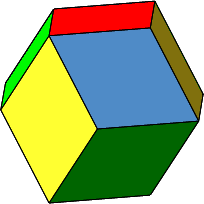
Abb. 1: Rhombendodekaeder
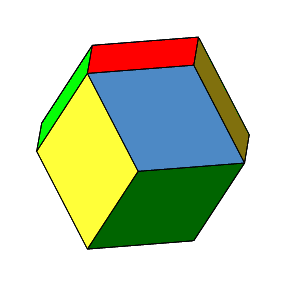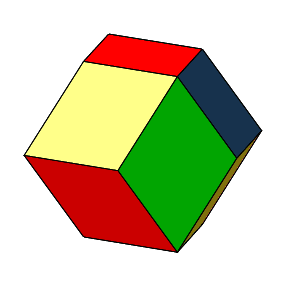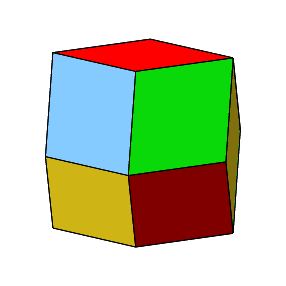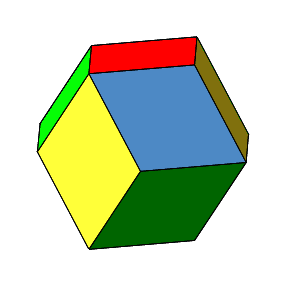
Abb. 2: Rhombendodekaeder von allen Seiten (wirklich von allen?)
Die Seitenrhomben (Abb. 3 gelber Rhombus in Frontalansicht) haben das Diagonalenverhältnis √(2):1 ≈ 1.414.
Der spitze Winkel der Rhomben ist arccos(⅓) ≈ 70.5288°. Dies ist der „kristallografische Winkel“, der in verschiedenen Kontexten der Kristallografie erscheint. Er ist auch der Diederwinkel (Winkel zwischen zwei aneinanderstoßenden Seitenflächen) des regelmäßigen Tetraeders.
Der Diederwinkel des Rhombendodekaeders ist 120°.
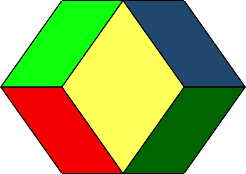
Abb. 3: Seitenrhombus
Das Rhombendodekaeder hat 14 Eckpunkte. Bei acht Eckpunkten stoßen je drei Rhomben mit ihren stumpfen Winkeln zusammen. Diese acht Eckpunkte sind auch die Ecken eines Würfels. Bei den restlichen sechs Eckpunkten stoßen je vier Rhomben mit ihren spitzen Winkeln zusammen. Diese sechs Eckpunkte sind auch die Ecken eines Oktaeders.
Das Rhombendodekaeder ist ein „space filler“, der Raum kann mit kongruenten Rhombendodekaedern lückenlos und ohne Überlappung ausgefüllt werden.
3 Das Bilinksi-Rhombendodekaeder
Das Rhombendodekaeder zweiter Art oder Bilinski-Rhombendodekaeder (Abb. 4 und 5, Foto 1) wurde von Stanko Bilinski 1960 beschrieben (Bilinski, 1960).
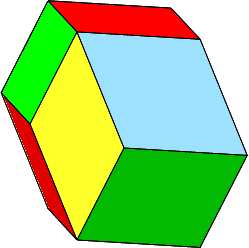
Abb. 4: Bilinski-Rhombendodekaeder
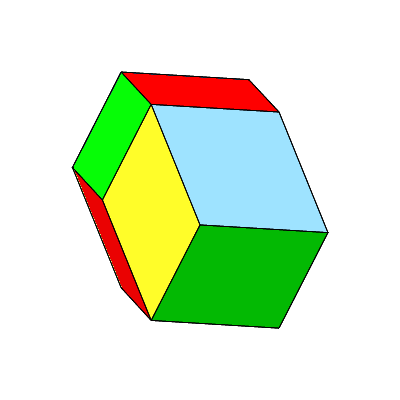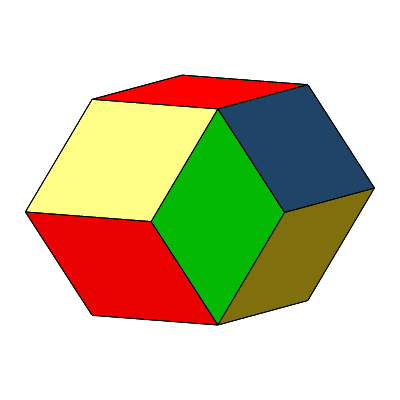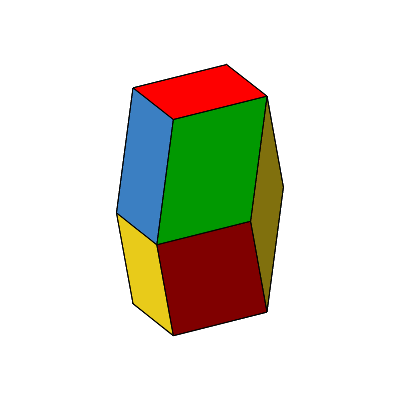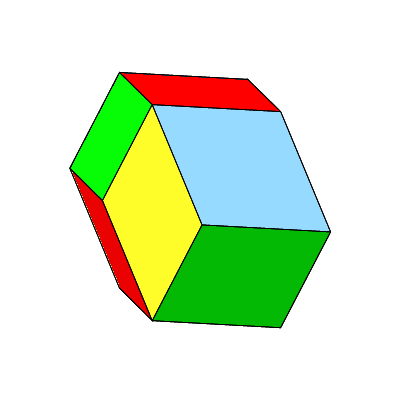
Abb. 5: Rotation des Bilinski-Rhombendodekaeders

Foto 1: Flechtmodell des Bilinski-Rhombendodekaeder
Die zwölf kongruenten Seitenrhomben (Abb. 6 gelber Rhombus in Frontalansicht) haben das Diagonalenverhältnis Φ:1 ≈ 1.618. Dabei ist Φ der Goldene Schnitt (Walser 2013).
Der spitze Winkel der Rhomben ist arctan(2) ≈ 63.435°.
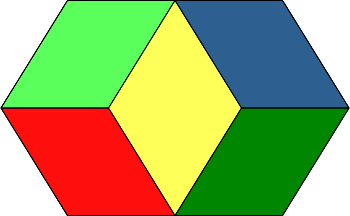
Abb. 6: Seitenrhombus
Es kommen drei verschiedene Diederwinkel vor, nämlich 72°, 108° und 144°. Diese können in speziellen Sichten (Blick parallel zur Kante) gesehen werden.
In der Abbildung 7.1 sind im Umriss die Diederwinkel 72° und 144° unverzerrt sichtbar.

Abb. 7.1: Winkel 72° und 144° sichtbar
In der Abbildung 7.2 sind im Umriss die Winkel 108° und 144° unverzerrt sichtbar.
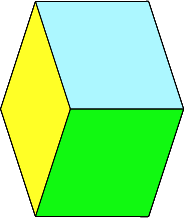
Abb. 7.2: Winkel 108° und 144° sichtbar
Das Bilinski-Rhombendodekaeder ist ebenfalls ein space filler.
4 Das nicht konvexe Bilinski-Rhombendodekaeder
Es gibt nun auch ein Rhombendodekaeder, das aus denselben zwölf kongruenten Rhomben wie das Bilinski-Rhombendodekaeder zusammengesetzt ist, aber Selbstüberschneidungen enthält und daher nicht konvex ist (Abb. 8 und 9, Foto 2 und 3).
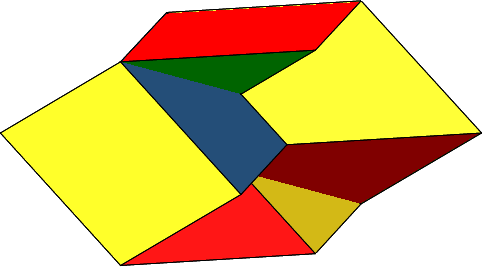
Abb. 8: Nicht konvexes Bilinski-Rhombendodekaeder
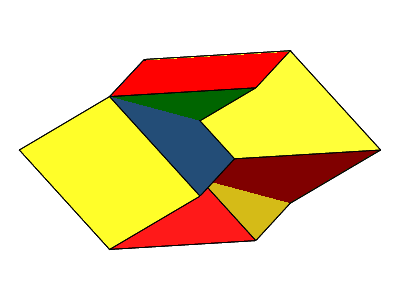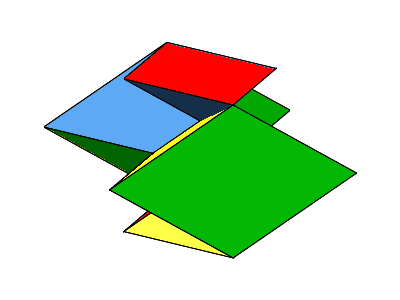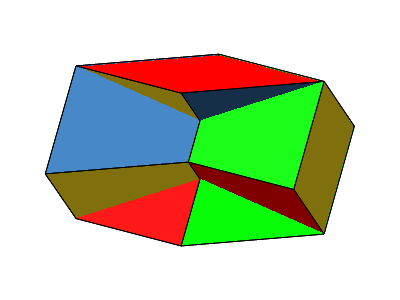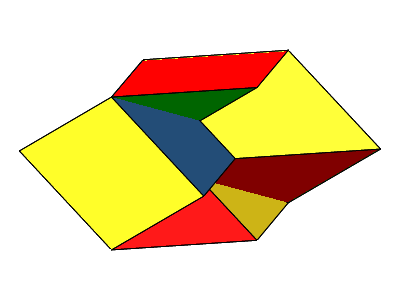
Abb. 9: Rotierendes nicht konvexes Bilinski-Rhombendodekaeder

Foto 2: Papiermodell des Bilinski-Rhombendodekaeder

Foto 3: Andere Sicht des Papiermodells
5 Überschneidung
Um die Situation der Überschneidung einzusehen, greifen wir zunächst zurück zum konvexen Bilinski-Rhombendodekaeder (Abb. 4 und 5, Foto 1). Die Abbildung 10a zeigt das Ecken-Kanten-Gerüst mit zwei eingepassten Rhomben (grün und blau).
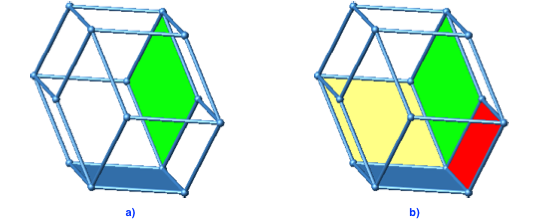
Abb. 10: Gerüst mit eingepassten Rhomben
Nun passen wir an der gemeinsamen Ecke zwei weitere Rhomben ein (Abb. 10b, rot und gelb). Jeder der beiden neu eingepassten Rhomben hat je eine Kante mit dem grünen und dem blauen Rhombus gemeinsam. Insgesamt entsteht so eine konvexe Ecke.
Analog verfahren wir im Gerüst des nicht konvexen Bilinski-Rhombendodekaeders (Abb. 8 und 9, Foto 2 und 3). In der Abbildung 11a haben wir zunächst den grünen und den blauen Rhombus.
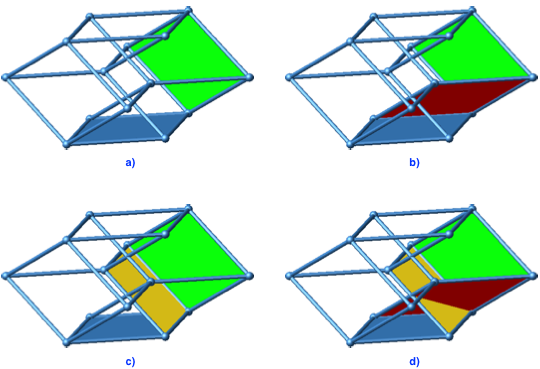
Abb. 11: Nicht konvexes Bilinski-Rhombendodekaeder
Wir passen wiederum einen roten Rhombus ein, der je eine Kante mit dem blauen und dem grünen Rhombus gemeinsam hat (Abb. 11b). Aber, und das ist jetzt der entscheidende Unterschied, nun geht es „übers Kreuz“. Entsprechend kann auch der gelbe Rhombus übers Kreuz eingepasst werden (Abb. 11c). Der gelbe und der rote Rhombus überschneiden sich (Abb. 11d).
Es gibt nun aber ein Problem mit der Orientierung bezüglich „innen“ und „außen“. Wenn wir mal naiverweise die uns zugewandte sichtbare Seite des grünen Rhombus als „innen“ ansehen und diese Innenheit auf die beiden anschließenden roten und gelben Rhomben übertragen, ist nach der Schnittgerade dieser beiden Rhomben die definierte Innenseite außen und die definierte Außenseite innen. Übertragen auf den blauen Rhombus heißt das, dass die uns zugewandte obere Seite die definierte Außenseite ist. Beim Übergang vom grünen Rhombus über die gemeinsame Ecke zum blauen Rhombus wechseln also „innen“ und „außen“ ihre Rollen. Man kann das so sehen, dass an der gemeinsamen Ecke der beiden Rhomben der blaue Rhombus um 180° gedreht gesehen werden muss. Wir haben einen Twist.
Wenn man solche Twists an den Ecken zulässt, ist das nicht konvexe Bilinsiki-Rhombendodekaeder konsistent orientierbar. Wir haben also nicht die Situation etwa eines Möbius-Bandes.
Ein Folgeproblem ist die Frage der Definition der Diederwinkel. Der innenliegende und der außenliegende Diederwinkel ergänzen sich auf 360°. Allerdings spricht das für die Zwischenwinkelberechnung üblicherweise verwendete Verfahren auf solche Subtilitäten nicht an. Das Verfahren gibt den kleineren der beiden Winkel. Ich habe rechnerisch die drei Diederwinkel 36°, 108° und 144° erhalten.
6 Gerüste
Die Abbildung 12a zeigt das Ecken-Kanten-Gerüst des konvexen Bilinski-Rhombendodekaeders, die Abbildung 12b jenes des nicht konvexen Falles. Beim konvexen Bilinski-Rhombendodekaeder können wir durch jeden Eckpunkt eine Ebene so legen, dass die ganze Figur auf einer Seite der Ebene liegt. Im nicht konvexen Fall gibt es zwei Ecken (diejenigen am nächsten zum Zentrum) wo dies nicht möglich ist.
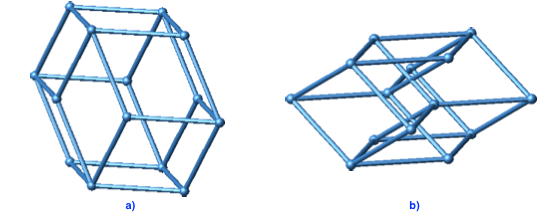
Abb. 12: Ecken-Kanten-Gerüste
Die beiden Gerüste haben dieselbe Topologie. Beide haben acht Knoten (Ecken), in welche je drei Kanten einmünden, und sechs Knoten mit je vier Kanten. (Das Gerüst des gewöhnlichen Rhombendodekaeders hat ebenfalls diese Topologie).
Hingegen sehen wir, dass diejenigen Rhomben, welche wir anschaulich als horizontal oder vertikal ansehen, beim Übergang vom konvexen zum nichtkonvexen Beispiel um 90° gedreht werden.
7 Ausblick
Auch zum üblichen Rhombendodekaeder gibt es eine nicht konvexe Entsprechung.
Weblinks
Hans Walser: Rhombentriakontaeder
http://www.walser-h-m.ch/hans/Miniaturen/R/Rhombentriakontaeder1/Rhombentriakontaeder1.html
Literatur
Bilinski, Stanko (1960): Über Rhombenisoeder. Glasnik mat.-fiz. i astr. 15, 1960, No. 4, S. 251-262.
Walser, Hans (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wußing über populärwissenschaftliche Mathematikliteratur aus Leipzig. Edition am Gutenbergplatz, Leipzig. ISBN 978-3-937219-85-1.