Hans Walser, [20130101a]

Binomische Formel

1 Binomische Formel modulo Exponent

Die binomische Formel gehört zu den Grundlagen der humanistischen Bildung. Leider wird sie von den Schülern oft falsch verwendet, nämlich in der Form:

Wenn wir allerdings modulo 2 rechnen, ist diese Formel durchaus richtig. Wenn wir modulo 3 rechnen, gilt:

Wer jetzt allerdings denkt, er habe die Sache im Griff, irrt. Modulo 4 ist nämlich:

Dies gibt Anlass, die Koeffizienten anzusehen. (Die Modulzahl wächst von Zeile zu Zeile, es gibt also nicht die üblichen Fraktale wie bei einer festen Modulzahl.)

2 Tabelle

Im Folgenden die Tabelle

2.1 Rechteckdarstellung

n\k	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
0	1
1	1	1
2	1	0	1
3	1	0	0	1
4	1	0	2	0	1
5	1	0	0	0	0	1
6	1	0	3	2	3	0	1
7	1	0	0	0	0	0	0	1
8	1	0	4	0	6	0	4	0	1
9	1	0	0	3	0	0	3	0	0	1
10	1	0	5	0	0	2	0	0	5	0	1
11	1	0	0	0	0	0	0	0	0	0	0	1
12	1	0	6	4	3	0	0	0	3	4	6	0	1
13	1	0	0	0	0	0	0	0	0	0	0	0	0	1
14	1	0	7	0	7	0	7	2	7	0	7	0	7	0	1
15	1	0	0	5	0	3	10	0	0	10	3	0	5	0	0	1
16	1	0	8	0	12	0	8	0	6	0	8	0	12	0	8	0	1
17	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1

2.2 Wabendarstellung

Die Nullen sind durch leere Waben dargestellt.

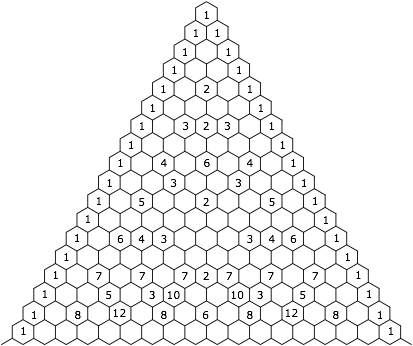
3 Vermutungen

Die Tabelle gibt Anlass zu einigen Vermutungen.

· Die Tabelle ist symmetrisch. . Trivial, da Binomialkoeffizienten symmetrisch.

· Für n prim haben wir in der entsprechenden Zeile eine „Nullenbank“. Zwischen der ersten und der letzten 1 hat es nur Nullen. Das lässt sich mit der Darstellung zeigen. Mit Ausnahme der ersten und der letzten Zahl lässt sich der prime Faktor n im Zähler nicht herauskürzen.

· Für k prim haben wir in der entsprechenden Spalte die natürlichen Zahlen mit jeweils Nullen dazwischen. Beweis für mich offen.

Link

http://oeis.org/A053200 (abgerufen 1.1.2013)