Hans Walser, [20180927]

Binomialkoeffizienten

1 Worum geht es?

Die Binomialkoeffizienten werden ins Negative fortgesetzt.

2 Was man in der Schule lernt

Wir expandieren die Potenzen des Binoms (a + b):

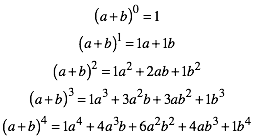(1)

Die auftretenden Koeffizienten heißen Binomialkoeffizienten. Die Abbildung 1 gibt das Koeffizientenschema bis zum Exponenten n = 10. Das Schema wird als Pascalsches Dreieck bezeichnet.

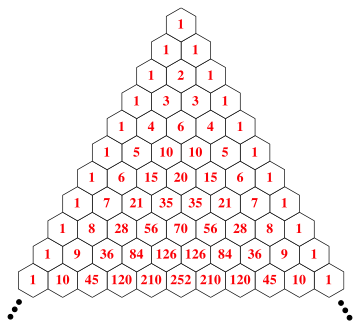
Abb. 1: Pascalsches Dreieck

Die Binomialkoeffizienten werden mit bezeichnet, wobei n der Zeilenindex ist, an der Spitze mit null beginnend, und k innerhalb einer Zeile der Laufindex, ebenfalls mit null beginnend.

Die binomischen Formeln gemäß (1) können damit formal geschrieben werden wie folgt:

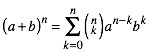(2)

Dabei ist:

(3)

Weiter gilt die Rekursionsformel:

(4)

Diese lässt sich im Wabenmusters visualisieren gemäß Abb. 2.

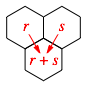
Abb. 2: Rekursion

3 Die große Leere

Wir denken uns das Wabenmuster der Abbildung 1 erweitert und die Waben links und rechts mit Nullen aufgefüllt. Damit genügen auch die Einsen in den Dachschrägen des Dreiecks der Abbildung 1 der Rekursion (4) — mit Ausnahme der Eins an der Spitze für n = 0.

Nun können wir die binomische Formel (2) schreiben:

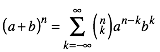(5)

Das ist natürlich ein Popanz, da nur Nullen dazukommen.

4 Die Ausnahme

Die Eins an der Spitze ergibt sich nicht aus der Rekursion. Für diese Eins an der Spitze ist ein eigener kleiner Schöpfungsakt oder ein Urknällchen erforderlich. Man kann auch von einem „Startwert“ reden.

Die Problematik kann verlagert werden, wenn wir in die beiden Waben links und rechts oberhalb der Spitzen-Eins je eine Zahl setzen, die zusammen eins ergeben. Allerdings müssen dann auch diese beiden Zahlen in die Rekursion eingebunden werden. Geht das?

5 Fortsetzung ins Negative

Wir nennen die beiden Zahlen p und q mit der Bedingung p + q = 1.

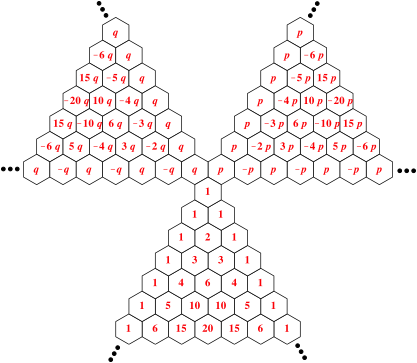
Abb. 3: Fortsetzung ins Negative

Die Abbildung 3 zeigt eine Lösung der Fortsetzung der Binomialkoeffizienten ins Negative. Wir erkennen die üblichen Binomialkoeffizienten, alternierend mit einem Minuszeichen versehen. Die Felder zwischen den Dreiecken sind mit Nullen gefüllt.

Da p frei gewählt werden kann, haben wir schon unendlich viele Lösungen. Ich vermute, dass es noch andere Lösungen gibt.

6 Formale Potenzreihen

Die binomische Formel (5) gilt nun auch für negative n. Dabei müssen wir mit formalen Potenzreihen arbeiten, Konvergenzfragen werden nicht bearbeitet.

Wir illustrieren das am Beispiel n = –3. Aus der Abbildung 3 lesen wir ab:

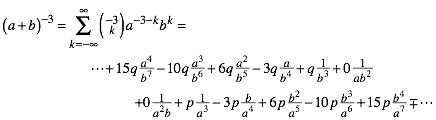(6)

Man beachte die Nullen in der Mitte. Das ist der Ort wo die Formel das weiße Feld zwischen den Dreiecken durchfährt.

Die Richtigkeit der Formel kontrollieren wir durch Rückmultiplikation. Es muss gelten:

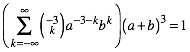(7)

Die Abbildung 4 zeigt den relevanten Ausschnitt des Rechenschemas von (7). Das Ergebnis ist p + q = 1.

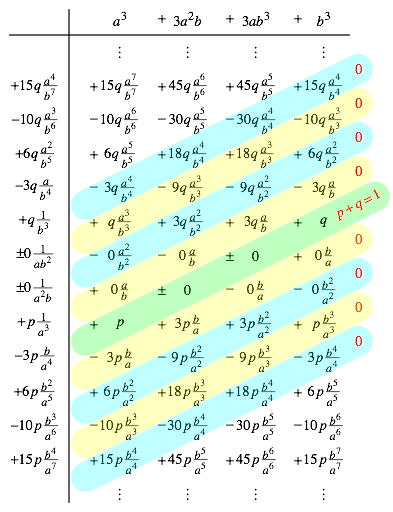
Abb. 4: Rechenschema

7 Symmetrie

Das Pascalsche Zahlendreieck der Abbildung 1 hat eine senkrechte Symmetrieachse. Damit auch die Fortsetzung ins Negative diese Symmetrie hat, muss gewählt werden (Abb. 5).

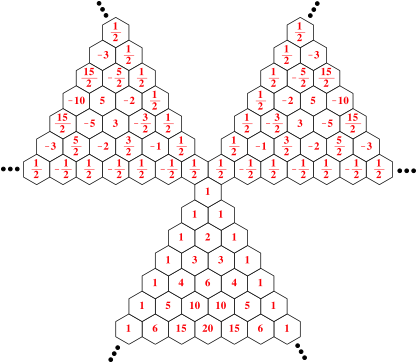
Abb.5: Symmetrische Version

8 Fibonacci-Zahlen

Geeignete Schrägzeilensummen im Pascalschen Dreieck ergeben die Fibonacci-Zahlen. Mit der Fortsetzung des Pascalschen Dreiecks vermöge q = 1 und p = 0 können wir die Fibonacci-Zahlen ins Negative fortsetzen (Abb. 6). Betragsmäßig sind es dieselben Zahlen, aber wir haben alternierende Vorzeichen. Die Fibonacci-Rekursion

(8)

ist durchgehend erfüllt.

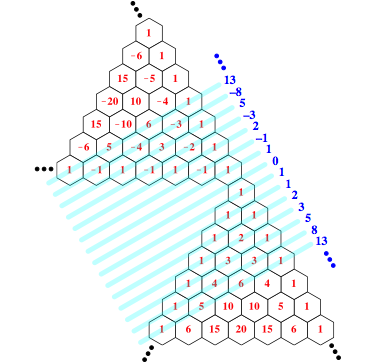
Abb. 6: Fortsetzung der Fibonacci-Zahlen

Mehr über Fibonacci-Zahlen siehe Walser (2012).

Literatur

Walser, Hans (2012): Fibonacci. Zahlen und Figuren. Leipzig, EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-60-8.