Hans Walser, [20210810]
Binomialkoeffizienten
0 Worum geht es?
Iteration der Rekursionsformel:
![]() (1)
(1)
1 Beispiel
Iteration von (1) ergibt:
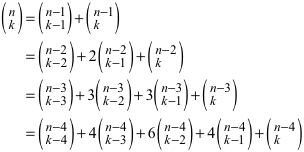 (2)
(2)
Wir erkennen als Koeffizienten wiederum die Binomialkoeffizienten, zum Beispiel bei Berechnung bis zur Tiefe 4:
![]() (3)
(3)
Nach (2) ist zum Beispiel:
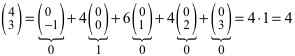 (4)
(4)
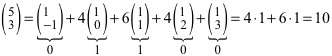 (5)
(5)
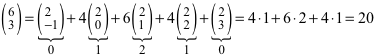 (6)
(6)
2 Allgemein
Rekursion bis zur Tiefe i:
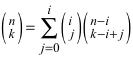 (7)
(7)
3 Sonderfälle
Sonderfall: i = k
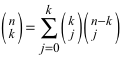 (8)
(8)
Sonderfall:
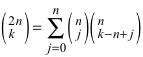 (9)
(9)
Sonderfall
im Sonderfall:
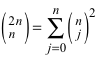 (10)
(10)
Sonderfall:
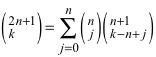 (11)
(11)
4 Illustration
Wir illustrieren exemplarisch die Formel (7). Die Abbildung 1 zeigt ein angefangenes Pascal-Dreieck der Binomialkoeffizienten.
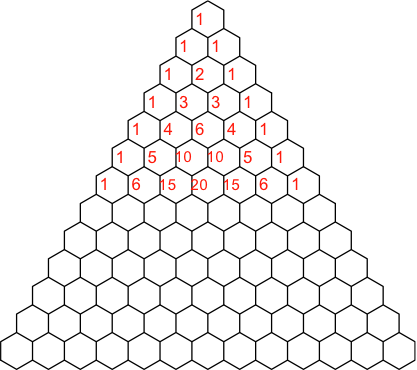
Abb. 1: Angefangenes Pascal-Dreieck
Die Zahlen sind an den linken Rand gesetzt, wir werden gleich sehen warum.
Die Abbildung 2 zeigt in blau dasselbe Dreieck, aber auf den Kopf gestellt.

Abb. 2: Blaues Dreieck
Wenn wir nun den Binomialkoeffizienten in einem bestimmten Feld berechnen wollen, legen wir das blaue Dreieck mit der unteren Spitze auf das betreffende Feld (Abb. 3). Man beachte, dass die roten und blauen Zahlen nun punktsymmetrisch angeordnet sind.
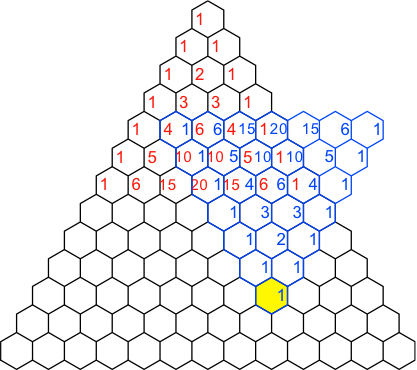
Abb. 3: Binomialkoeffizient im gelben Feld
Dann wählen wir im Überlappungsbereich der beiden Zahlendreiecke irgendeine Zeile aus und berechnen die Summe der der Produkte von je einer roten Zahl mit der blauen Zahl im selben Feld. Fehlt eine der beiden Zahlen, setzen wir null. Die Rechnung läuft also ab wie beim Skalarprodukt zweier Vektoren.
Für die oberste Zeile im Überlappungsbereich erhalten wir:
![]() (12)
(12)
Für die zweitoberste Zeile erhalten wir:
![]() (13)
(13)
Man beachte die palindromische Symmetrie der Rechnung. Die Mitte der Rechnung ist auch das Zentrum der Punktsymmetrie der roten und blauen Zahlen.
Und schließlich die letzte Zeile im Überlappungsbereich:
![]() (14)
(14)
Die Rechnung (14) ist spiegelbildlich zur Rechnung (12).
Der Binomialkoeffizient im gelben Feld ist:
![]() (15)
(15)
5 Sonderfälle
In der Abbildung 4 berechnen wir eine schon bekannte Zahl der untersten roten Reihe.
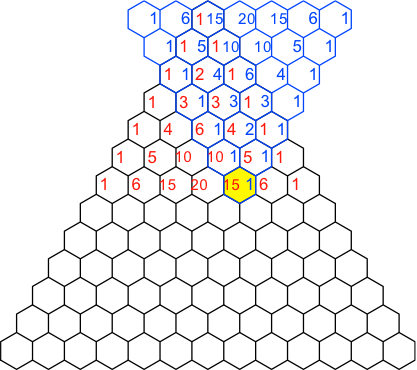
Abb. 4: Anschlag oben
Die Abbildung 5 illustriert exemplarisch den Sonderfall der Formel (10).
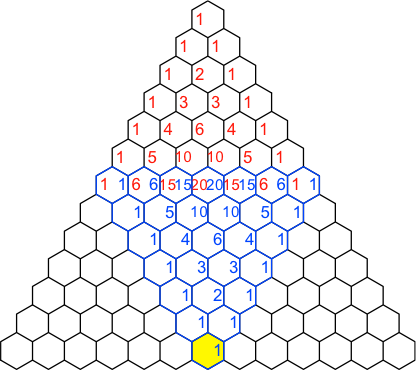
Abb. 5: Symmetrischer Sonderfall