Hans Walser, [20100916a]

Blumen und Sterne aus Kreisbšgen

Anregung: A. F., B.

1        Bilder

 

Blume

 

Stern

 

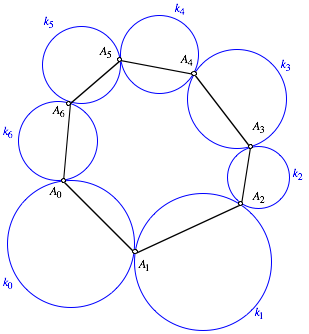
2        Definitionen

Zu n Punkten  (zyklische Indizierung modulo n) suchen wir n Kreisbšgen  derart dass sich die Bšgen  und  im Punkt  berŸhren, entweder mit einer Spitze nach innen (Blume) oder einer Spitze nach au§en (Stern).

3        Bearbeitung

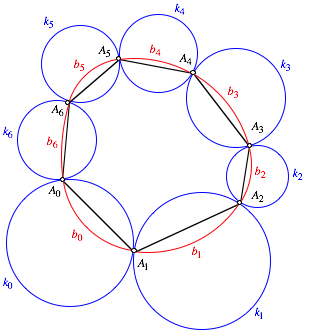
3.1      Kreiskette

Das Problem ist gelšst, wenn es gelingt, eine Kette von Kreisen  zu zeichnen, so dass sich die beiden Kreise  und  in  berŸhren.

 

Kreiskette

 

3.2      Umkorbbogen

Eine Kreiskette finden wir, sobald wir zu den n gegebenen Punkten einen so genannten Umkorbbogen haben.

 

Umkorbbogen

 

Der Umkorbbogen setzt sich aus einzelnen Kreisbšgen  zusammen, die an den †bergangspunkten  glatt ineinander Ÿbergehen.

(Allgemein: Eine Kurve, welche aus Kreisbšgen mit glatten †bergŠngen zusammengesetzt ist, wird als Korbbogen bezeichnet [Giering 1992].)

Der Kreis  der Kreiskette ist dann der Orthogonalkreis zum Bogen .

3.3      ParitŠtsunterscheidung

FŸr Existenz, Eindeutigkeit und Konstruktion von Umkorbbšgen von geschlossenen Polygonen  ist eine Fallunterscheidung bezŸglich der ParitŠt von n erforderlich (vgl. [Walser 1996]).

3.3.1    Ungerade Anzahl Punkte

Ein geschlossenes Polygon mit ungerader Eckenzahl n hat genau einen Umkorbbogen. Wir haben daher auch immer eine eindeutig bestimmte Blume und einen eindeutig bestimmten Stern. Bei einem Sehnenpolygon ist der Umkorbbogen der Umkreis. Bei einem Dreieck ist dies immer der Fall. Die Bilder oben zeigen aber ein Beispiel fŸr , das keinen Umkreis, wohl aber einen Umkorbbogen besitzt.

3.3.2    Gerade Anzahl Punkte

Bei einem geschlossenen Polygon mit gerader Eckenzahl n ist die alternierende Winkelsumme  ausschlaggebend. FŸr  gibt es keinen Umkorbbogen und damit weder Blume noch Stern. FŸr  gibt es unendlich viele Umkorbbšgen und entsprechend unendlich viele Blumen und Sterne.

3.3.2.1  Sehnenviereck

Ein Viereck mit verschwindender alternierender Winkelsumme ist ein Sehnenviereck. Der Umkreis ist ein mšglicher Umkorbbogen, es gibt aber auch andere. Die Abbildungen zeigen fŸr dasselbe Sehnenviereck die Situation mit dem Umkreis und mit einem anderen Umkorbbogen.

 

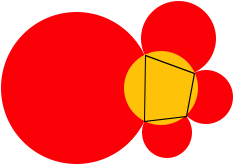
Sehnenviereck und Umkreis

 

    

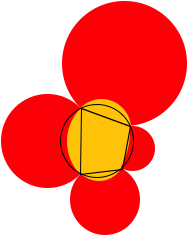
Variante: Sehnenviereck und Umkorbbogen

 

3.3.2.2  Sechseck

FŸr gerades  gibt es auch bei verschwindender alternierender Winkelsumme in der Regel keinen Umkreis. Wird zum Beispiel bei einem regelmŠ§igen Sechseck durch eine Parallele zu einer Seite ein Trapez abgeschnitten, bleibt ein gleichwinkliges, aber nicht gleichseitiges Sechseck Ÿbrig. Die alternierende Winkelsumme ist nach wie vor null, aber das Sechseck hat keinen Umkreis. Es hat aber unendlich viele Umkorbbšgen. Im Beispiel links wurde der halbe Umkreis des ursprŸnglichen regelmŠ§igen Sechsecks mit verwendet.

 

              

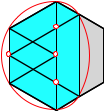
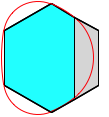
Umkorbbogen. Variante

 

Entsprechend haben wir unendlich viele Blumen und Sterne.

 

  

Blume und Stern

 

Blume und Stern, Variante

 

Literatur

[Giering 1992]            Giering, Oswald: Zur Geometrie der Polygon-Korbbšgen. PM, Praxis der Mathematik (34), 1992, S. 245-248.

[Walser 1996]            Walser, Hans: Geschlossene Korbbšgen. Praxis der Mathematik (38), 1996, S. 169-172.