Hans Walser, [20150324]

Brennpunkt und Leitlinie der Parabel

1     Worum geht es?

Eine Parabel sei durch fŸnf Punkte  gegeben (Abb. 1).

 

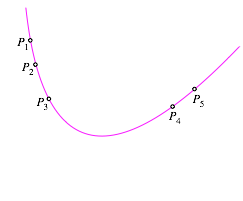
Abb. 1: Parabel durch fŸnf Punkte

 

Gesucht sind der Brennpunkt und die Leitlinie der Parabel. Gibt es ein Verfahren ohne Rechnen?

Bemerkung 1: Durch fŸnf Punkte kann auch eine Ellipse oder eine Hyperbel gegeben sein. Der Fall der Parabel ist ein †bergangsfall und daher sehr unwahrscheinlich.

FŸr den Fall der Ellipse siehe [Ellipse].

Wie es bei Hyperbeln geht, wei§ ich nicht.

Bemerkung 2: In den Abbildungen ist jeweils die Parabel magenta eingezeichnet. Dies hat aber rein dekorative Bedeutung. Die Parabel wird fŸr die Konstruktionen nicht verwendet.

Bemerkung 3: Im Folgenden wird das Konstruktionsverfahren beschrieben. Die Beweise Ÿberlassen wir dem der Lust hat.  

2     Pappos-Pascal

GemŠ§ dem Satz von Pappos-Pascal kann zu den fŸnf gegebenen Punkten auf beliebig viele Arten ein sechster Parabelpunkt konstruiert werden. Insbesondere kann dieser sechste Punkt auf einer frei wŠhlbaren Geraden durch einen der fŸnf gegebenen Punkte konstruiert werden. Wir kšnnen also zu jedem der gegebenen fŸnf Punkt eine Sehne in beliebiger Richtung zeichnen.

3     Achse zu schiefer Symmetrie

Parallel zur Sehne  zeichnen wir eine Sehne durch  (Abb. 2). Die Gerade durch die Mittelpunkte der beiden Sehnen ist Symmetrieachse der Parabel bei der SchrŠgspiegelung in Richtung der beiden Sehnen.

 

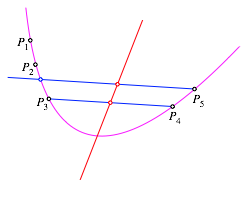
Abb. 2: Achse zu schiefer Symmetrie

 

Diese Achse ist parallel zur Ÿblichen Symmetrieachse (Orthogonalspiegelung) der Parabel.

4     Symmetrieachse der Parabel

Wir zeichnen nun durch  eine zur SchrŠgspiegelsymmetrieachse orthogonale Sehne. Die Mittelsenkrechte dieser Sehne ist die Ÿbliche Symmetrieachse der Parabel (Abb. 3). Man beachte, dass wir damit zwar die Symmetrieachse haben, aber noch nicht den Scheitelpunkt der Parabel.

 

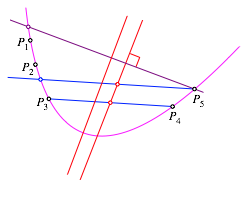
Abb. 3: Symmetrieachse der Parabel

 

5     Die EinheitslŠnge

Wir orientieren uns gedanklich an der durch  gegeben schulischen Parabel. Diese hat fŸr  eine Tangente der Steigung 1. Diese Tangente schlie§t mit der Symmetrieachse einen Winkel 45¡ ein.

Daher zeichnen wir durch  eine Sehne, welche mit der Symmetrieachse einen Winkel 45¡ einschlie§t (Abb. 4).

 

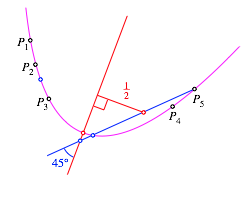
Abb. 4: Konstruktion der Einheit

 

Der Mittelpunkt dieser Sehne hat von der Symmetrieachse den Abstand . Durch Verdoppelung erhalten wir die Einheit des passenden schrŠgen kartesischen Koordinatensystems.

6     Scheitelpunkt

Wir zeichnen nun ein Quadrat mit einer Ecke in  und einer Seite auf der Symmetrieachse (Abb. 5).

 

 

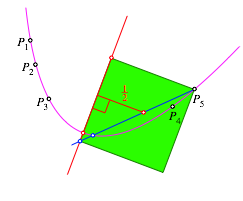
Abb. 5: Quadrat

 

Dieses Quadrat verwandeln wir nun in ein flŠchengleiches Rechteck mit der Einheit als einer Seite. Die dazu senkrechte Seite soll auf der Symmetrieachse liegen. Die Oberkante des Rechteckes soll durch  verlaufen (Abb. 6). Die untere Rechteckecke auf der Symmetrieachse ist der Scheitelpunkt der Parabel.

 

Abb. 6: Rechteck und Scheitelpunkt

 

7     Brennpunkt und Leitlinie

Der Brennpunkt der Parabel liegt nun auf der Symmetrieachse im Abstand  oberhalb des Scheitelpunktes (Abb. 7). Die Leitlinie ist orthogonal zur Symmetrieachse und schneidet diese im Abstand  unterhalb des Scheitelpunktes.

 

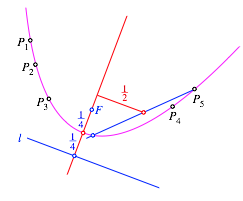
Abb. 7: Brennpunkt und Leitlinie

 

 

Websites

[Ellipse]. Abgerufen 4. 4. 2015

http://www.walser-h-m.ch/hans/Miniaturen/B/Brennpunkte_Ellipse/Brennpunkte_Ellipse.htm

http://www.walser-h-m.ch/hans/Miniaturen/B/Brennpunkte_Ellipse/Brennpunkte_Ellipse.pdf