Hans Walser, [20150318]
Brennpunkte der Ellipse
1 Worum geht es?
Eine
Ellipse sei durch fźnf Punkte ![]() gegeben
(Abb. 1).
gegeben
(Abb. 1).

Abb. 1: Eine Ellipse durch fźnf Punkte
Gesucht sind die Brennpunkte der Ellipse. Gibt es ein Verfahren ohne Rechnen?
Bemerkung 1: durch fźnf Punkte kann auch eine Hyperbel oder eine Parabel gegeben sein. Wir konzentrieren uns zunŠchst auf den Fall der Ellipse. Wie es bei Hyperbeln oder Parabeln geht, wei§ ich nicht.
Bemerkung 2: In den Abbildungen ist jeweils die Ellipse magenta eingezeichnet. Dies hat aber rein dekorative Bedeutung. Die Ellipse wird fźr die Konstruktionen nicht verwendet.
Bemerkung 3: Im Folgenden wird das Konstruktionsverfahren beschrieben. Die Beweise źberlassen wir dem der Lust hat.
2 Pappos-Pascal
GemŠ§ dem Satz von Pappos-Pascal kann zu den fźnf gegebenen Punkten auf beliebig viele Arten ein sechster Ellipsenpunkt konstruiert werden. Das geht so (Abb. 2).
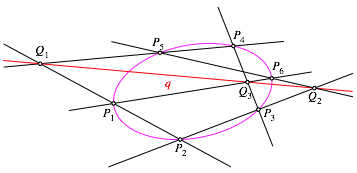
Abb. 2: Sechster Punkt
![]() sei der Schnittpunkt der Geraden
sei der Schnittpunkt der Geraden ![]() und
und ![]() . Durch
. Durch ![]() legen wir
eine beliebige Gerade q (hier haben
wir einen Freiheitsgrad).
legen wir
eine beliebige Gerade q (hier haben
wir einen Freiheitsgrad). ![]() sei der
Schnittpunkt von
sei der
Schnittpunkt von ![]() mit q.
mit q. ![]() sei der
Schnittpunkt von
sei der
Schnittpunkt von ![]() mit q. Die Geraden
mit q. Die Geraden ![]() und
und ![]() schneiden
sich in einem Punkt
schneiden
sich in einem Punkt ![]() , und dies ist ein weiterer Ellipsenpunkt.
, und dies ist ein weiterer Ellipsenpunkt.
In unserer
Konstruktion war die Gerade q
beliebig durch ![]() gewŠhlt
worden.
gewŠhlt
worden.
3 Modifikation
Die Abbildung 3 zeigt eine Modifikation.
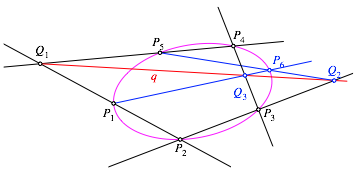
Abb. 3: Modifikation
Wir
wŠhlen durch ![]() eine
beliebige Gerade (in Abb. 3 blau gezeichnet).
eine
beliebige Gerade (in Abb. 3 blau gezeichnet). ![]() sei nun
der Schnittpunkt dieser blauen Geraden mit
sei nun
der Schnittpunkt dieser blauen Geraden mit ![]() . Weiter sei
. Weiter sei ![]() der
Schnittpunkt von
der
Schnittpunkt von ![]() mit
mit ![]() . Der Schnittpunkt
. Der Schnittpunkt ![]() von (das ist die blaue Gerade)
von (das ist die blaue Gerade) ![]() mit
mit ![]() ist nun
der sechste Ellipsenpunkt.
ist nun
der sechste Ellipsenpunkt.
Wir kšnnen also zu einem der fźnf Startpunkte in beliebiger Richtung einen sechsten Ellipsenpunkt finden.
4 Eine Achse
Wir
zeichnen durch ![]() und
und ![]() zwei
parallele Geraden und darauf je einen weiteren Ellipsenpunkt
zwei
parallele Geraden und darauf je einen weiteren Ellipsenpunkt ![]() beziehungsweise
beziehungsweise ![]() (Abb. 4,
die Detailkonstruktionen sind nicht angegeben).
(Abb. 4,
die Detailkonstruktionen sind nicht angegeben). ![]() und
und ![]() seien die
Mittelpunkte der Strecken
seien die
Mittelpunkte der Strecken ![]() respektive
respektive
![]() . Die Gerade
. Die Gerade ![]() ist eine
Achse der Ellipse, das hei§t, eine Gerade, welche durch den Mittelpunkt der
Ellipse verlŠuft. Hintergrund: affines Bild eines Kreises.
ist eine
Achse der Ellipse, das hei§t, eine Gerade, welche durch den Mittelpunkt der
Ellipse verlŠuft. Hintergrund: affines Bild eines Kreises.
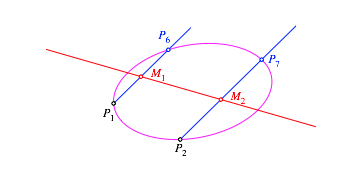
Abb. 4: Achse
5 Mittelpunkt der Ellipse
Wir konstruieren nun noch eine zweite Achse (Abb. 5). Der Schnittpunkt der beiden Achsen ist der Mittelpunkt M der Ellipse.
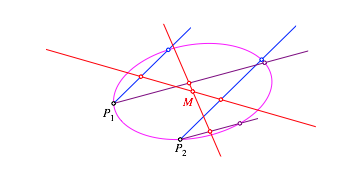
Abb. 5: Mittelpunkt
6 Konjugierte Durchmesserrichtungen
Durch den Mittelpunkt M legen wir eine Parallele zu den Richtungen, welche wir bei der Konstruktion der ersten Achse verwendet haben (Abb. 6). Diese Parallele und die erste Achse haben konjugierte Durchmesserrichtungen.

Abb. 6: Konjugierte Durchmesserrichtungen
Leider haben wir nur die Richtungen der konjugierten Durchmesser und nicht die Durchmesser selbst. Wir sind also noch nicht źber dem Berg.
7 Durchmesser
Um die Endpunkte der konjugierten Durchmesser zu finden, verfahren wir wie folgt. Wir starten mit der Konfiguration mit der Achse c der Abbildung 7, welche auf der Abbildungen 4 und 6 basiert.
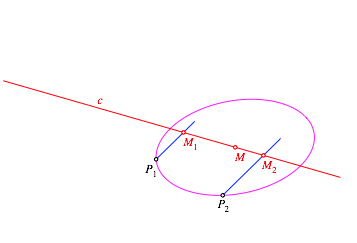
Abb. 7: Ausgangslage
Es sei Q der Schnittpunkt der Achse c mit der Geraden ![]() . Zur Strecke QM
zeichnen wir den Thaleskreis (Abb. 8).
. Zur Strecke QM
zeichnen wir den Thaleskreis (Abb. 8).
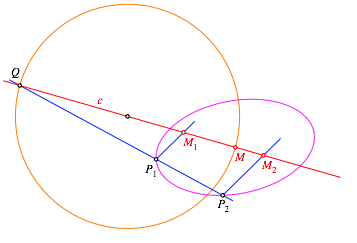
Abb. 8: Thaleskreis
Weiter
sei nun N der Mittelpunkt der Strecke
![]() und R der Schnittpunkt des Lotes in N auf c mit dem Thaleskreis (Abb. 9).
und R der Schnittpunkt des Lotes in N auf c mit dem Thaleskreis (Abb. 9).
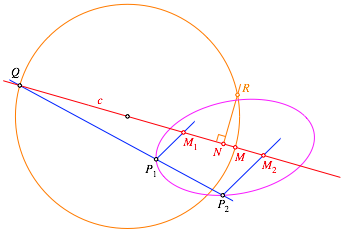
Abb. 9: Schnittpunkt mit Lot
In ![]() errichten
wir ebenfalls das Lot auf c und
schneiden dieses mit der Geraden QR.
Das gibt den Schnittpunkt S (Abb.
10).
errichten
wir ebenfalls das Lot auf c und
schneiden dieses mit der Geraden QR.
Das gibt den Schnittpunkt S (Abb.
10).
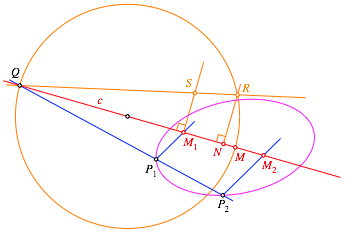
Abb. 10: Schnittpunkt
Die
beiden Schnittpunkte ![]() und
und ![]() des
Kreises um M durch S mit der Achse c sind Ellipsenpunkte und daher die Endpunkte des
Ellipsendurchmessers auf der Achse c
des
Kreises um M durch S mit der Achse c sind Ellipsenpunkte und daher die Endpunkte des
Ellipsendurchmessers auf der Achse c
(Abb. 11).
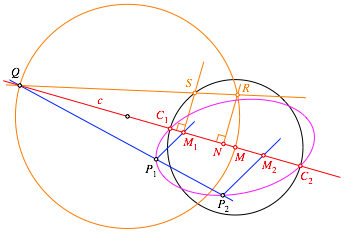
Abb. 11: Ellipsendurchmesser
8 Konjugierte Durchmesser
Wir ergŠnzen nun gemŠ§ Abbildung 12.
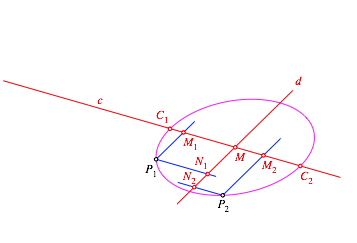
Abb. 12: ErgŠnzung
Damit kšnnen wir analog die LŠnge des konjugierten Durchmessers bestimmen (Abb.13).
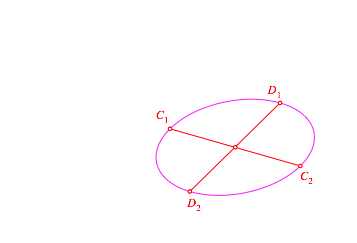
Abb. 13: Konjugierte Durchmesser
9 Halbachsen
Nun kšnnen wir mit dem Verfahren von Rytz die Halbachsen konstruieren (Abb. 14).
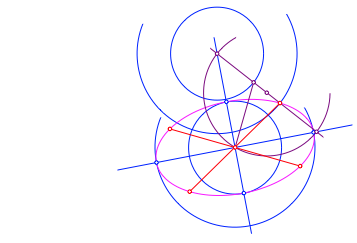
Abb. 14: Halbachsen
10 Brennpunkte
Damit
finden wir schlie§lich die Brennpunkte ![]() und
und ![]() (Abb. 15).
(Abb. 15).
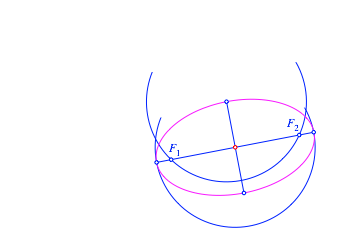
Abb. 15: Brennpunkte