1 Worum geht es?

Neue Sicht auf die Ellipse

Verallgemeinerung der Konchoide

2 Die Ellipse wie gehabt

So lernt man es in der Schule: An zwei festen Brennpunkten F und G (Abb. 1) befestigen wir die beiden Enden einer Schnur, welche länger ist als der Abstand der beiden Brennpunkte. Nun ziehen wir mit dem Zeichenstift P die Schnur straff zum Dreieck FGP. Variation von P generiert die Ellipse.

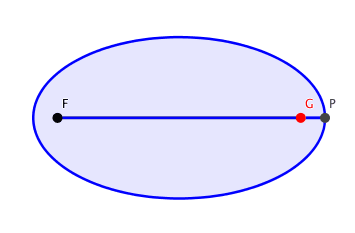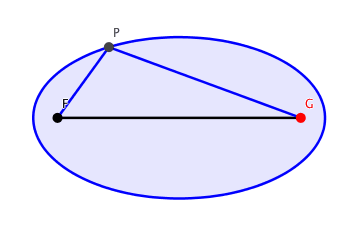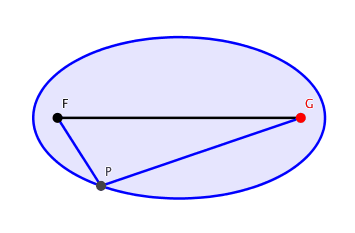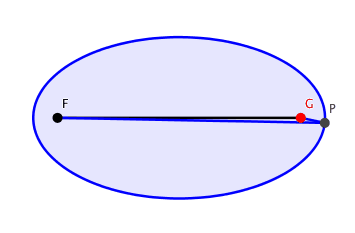
Abb. 1: Ellipse

3 Umkehrung der Sichtweise

Wir halten den Punkt P fest, den Punkt F lassen wir auf einer beliebigen Leitkurve variieren. In der Abbildung 2a ist die Leitkurve ein Kreis. Im Punkt F ist drehbar das eine Ende eines Stabes (einer Strecke) befestigt. Ebenso ist im Punkt F das eine Ende einer Schnur befestigt, welche länger als der Stab ist. Die Schnur ziehen wir durch eine Öse im Punkt P und befestigen das zweite Ende der Schnur am Endpunkt G des Stabes (Abb. 2b) und ziehen straff. Von den beiden symmetrischen Lösungen wählen wir diejenige, bei der das Dreieck FGP einen positiven Umlaufsinn hat.

Nun liegt P auf der Ellipse mit den Brennpunkten F und G und der Abstandssumme der Schnurlänge (Abb. 2c).

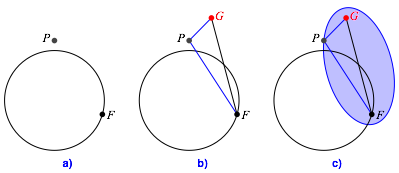
Abb. 2: Fadenkonstruktion

4 Bahnkurve des zweiten Brennpunktes

Die Abbildung 3 zeigt die Bahnkurve des Brennpunktes G.

Abb. 3: Bahnkurve

Wenn wir auch den negativen Umlaufsinn für das Dreieck FGP zulassen, ergibt sich eine symmetrische Bahnkurve (Abb. 4).

Abb. 4: Symmetrische Bahnkurve

5 Variation der Schnurlänge

Im Beispiel der Abbildungen 1 bis 4 haben wir mit dem Brennpunktabstand 2 und der Schnurlänge 2.4 gearbeitet.

In der Abbildung 5 ist der Brennpunktabstand immer noch 2, die Schnurlänge variiert aber von 2 bis 8.

Abb. 5: Variation der Schnurlänge

6 Sonderfall Konchoide

Wir wählen die Schnurlänge gleich dem Brennpunktabstand. Damit wird die Ellipse zum Grenzfall einer Strecke.

Die Bahnkurve des Punktes G ist die Konchoide mit dem Kreis, auf dem F variiert, als Leitlinie und dem Punkt P als Pol (Abb. 6).

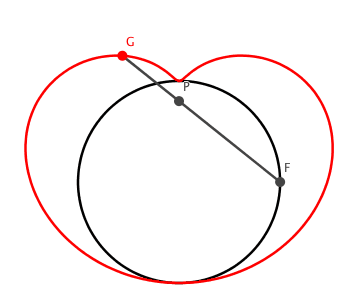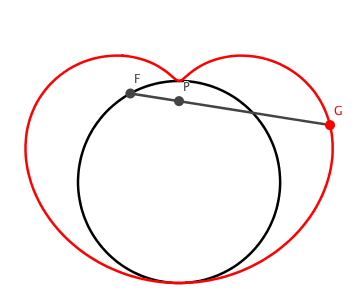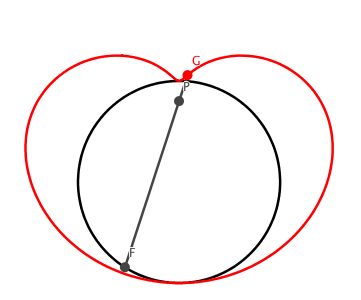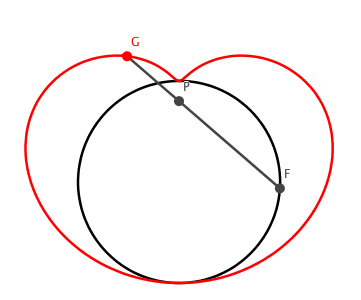
Abb. 6: Konchoide

Literatur

Haftendorn, Dörte (2017): Kurven erkunden und verstehen. Mit GeoGebra und anderen Werkzeugen. Wiesbaden: Springer Spektrum. ISBN 978-3-658-14748-8.

Website

Hans Walser: Bananenkurve

http://www.walser-h-m.ch/hans/Miniaturen/B/Bananenkurve/Bananenkurve.htm