Hans Walser, [20180112], [20220624]

Brotkruste

Anregungen: Sebastian Baader, Bern, und Anselm Lambert, Saarbrücken

1 Worum geht es?

In einigen Gegenden der Schweiz gibt es ein annähernd kugelförmiges Brot, das so genannte St. Galler-Brot (Abb. 1).

Abb. 1: St. Galler-Brot (stilisiert)

Da bei gut gebackenem Brot die Kruste als Leckerbissen gilt, ist die Frage, wie aus Gerechtigkeitsgründen das Brot in Scheiben zu schneiden ist so dass alle Scheiben gleich viel Kruste enthalten.

Die Antwort ist einfach: Die Brotscheiben müssen gleich dick sein.

2 Begründung

Wir modellieren das St. Galler-Brot als Kugel. Die Kruste einer Scheibe ist eine Kugelzone.

2.1 Formelsammlung

In der Formelsammlung finden wir für den Flächeninhalt A einer Kugelzone:

(1)

Dabei ist R der Kugelradius und h die Höhe, also die Scheibendicke. Wie kann diese Formel hergeleitet werden?

2.2 Die Karte von Archimedes-Lambert

Archimedes (Archimedes von Syrakus, um 287 v. Chr. – 212 v. Chr.) schlug vor, eine Weltkarte wie folgt zu zeichnen. Um den Äquator der Erdkugel legt er einen Zylinder, der gleich hoch ist wie die Erde (Abb. 2a). Dann projiziert er einen Kugelpunkt (grün in Abb. 2b) von der Erdachse aus horizontal auf den Zylinder (roter Bildpunkt in Abb. 2b).

Das gelbe Dreieck ist rechtwinklig. Seine Hypotenuse ist der Erdradius R, seine horizontale Kathete ist der Radius r des Breitenkreises, auf dem sich der grüne Kugelpunkt befindet.

Nach der Projektion wird der Zylinder längs einer Mantellinie (Bild eines Meridians) aufgeschnitten und in die Ebene abgerollt. Das gibt ein Rechteck der Länge (Länge des Äquators) und der Höhe (Höhe von Pol zu Pol).

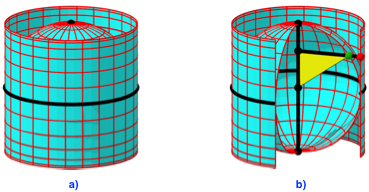
Abb. 2: Vorschlag von Archimedes

Die Abbildung 3 zeigt die nach diesem Verfahren hergestellte Weltkarte. Sie wird als Karte von Archimedes-Lambert bezeichnet (Johann Heinrich Lambert, 1728-1777). Kartendaten aus [1] .

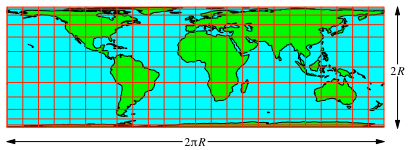
Abb. 3: Karte von Archimedes-Lambert

2.3 Flächengleichheit

Die Fläche des Rechteckes mit der Länge und der Höhe ist , also gleich groß wie die Kugeloberfläche.

Zudem ist es so — und das ist das Raffinierte an dieser Karte — dass nicht nur die globale Fläche übereinstimmt, sondern dass auch jedes Detail flächenmäßig übereinstimmt. So ist zum Beispiel jeder Kontinent auf der Karte in der richtigen Größe angegeben. Allerdings werden die Formen der Kontinente verzerrt.

Um zu zeigen, dass jede Detailfläche in der richtigen Größe wiedergegeben wir, denken wir uns auf der Erdkugel ein kleines, nach Norden ausgerichtetes Quadrat der Seitenlänge s.

In der Süd-Nord-Richtung wird diese Seitenlänge bei der Projektion von Archimedes gestaucht (Abb. 4). Die gestauchte Länge bezeichnen wir mit .

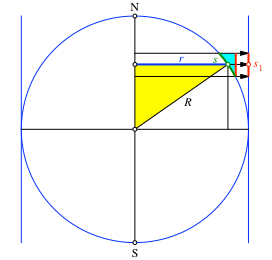
Abb. 4: Stauchen in Süd-Nord-Richtung

Da die beiden in der Abbildung 4 eingezeichneten Dreiecke ähnlich sind, gilt:

(2)

In der West-Ost-Richtung wird die Seitenlänge aber gespreizt. Die Abbildung 5 zeigt die Situation in der Sicht von oben. Die gespreizte Länge bezeichnen wir mit .

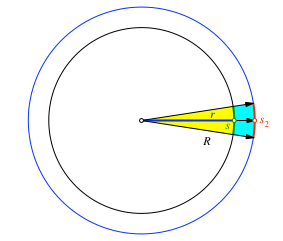
Abb. 5: Spreizen in der West-Ost-Richtung

Wir sehen zwei teilweise übereinander liegende Sektoren. Der kleine Sektor (gelb) hat den Radius r und den Bogen s. Der große Sektor (hellblau) hat den Radius R und den Bogen . Aus der Ähnlichkeit der beiden Sektoren folgt:

(3)

Das kleine Quadrat mit der Seitenlänge s wird also auf ein Rechteck mit den Seiten und abgebildet (Abb. 6). Da sehen wir nochmals, dass die Form verzerrt wird.

Abb. 6: Aus dem Quadrat wird ein Rechteck

Für den Flächeninhalt dieses Rechteckes erhalten wir aus (2) und (3):

(4)

Das kleine Quadrat und sein rechteckiges Bild auf der Karte haben also den gleichen Flächeninhalt. Wenn wir also zum Beispiel Australien in kleine Quadrate zerlegen, ergibt sich auf der Karte eine Zerlegung in kleine Rechtecke mit derselben Fläche.

Zum Nachdenken: Kann man wirklich Australien in kleine Quadrate zerlegen?

2.4 Kugelzone

Wir projizieren nun eine Kugelzone nach dem Verfahren von Archimedes (Abb. 7 und 8).

Abb. 7: Kugelzone

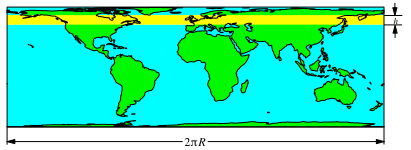
Abb. 8: Kugelzone in der Karte

Für den Flächeninhalt A der gelben Kugelzone erhalten wir wie in (1).

3 Infinitesimal klein

Bei unserer Flächenüberlegung mit dem „kleinen“ Quadrat sind wir darüber hinweggegangen, dass auch ein kleines Quadrat auf der Kugel nicht eben ist. Die Flächenüberlegungen gelten daher nur näherungsweise. Allerdings wird diese Näherung immer besser, je kleiner das Quadrat ist. Das führt zum Konzept eines „unendlich kleinen“ oder infinitesimal kleinen Quadrates. Solche Überlegungen gehen auf Leibniz (Gottfried Wilhelm Leibniz, 1646-1716) zurück und markieren den Beginn der formalen Infinitesimalrechnung. Wir haben aber gesehen, wie dies bereits Archimedes implizit gehandhabt hat.

4 Welches ist die rundeste Kugel?

4.1 Frage und Antwort

Abb. 9: Welches ist die rundeste Kugel?

In der Regel wird die Kugel der Abbildung 9b als rundeste oder schönste Kugel bezeichnet. Eine Minderheit gibt der Kugel der Abbildung 9a den Vorzug. Ein einziges Mal habe ich erlebt dass jemand (ein Künstler, der nebenbei Mathematik für das Lehramt studierte) die Kugel der Abbildung 9c als schönste ansah.

4.2 Form und Fläche

Die Meridiane sind in allen drei Bildern gleich eingezeichnet. Unterschiede bestehen lediglich in der Darstellung der Breitenkreise.

Bei der Kugel der Abbildung 9a wurde die übliche Parametrisierung mit geografischer Breite und geografischer Länge mit einer Maschengröße (Schrittlänge) von 15° verwendet. Diese Darstellungstechnik soll bereits den Phöniziern bekannt gewesen sein. Die Netzvierecke sind, auf der Kugeloberfläche gemessen, alle gleich hoch, in unserem Beispiel 15°. Die Breitenkreise bilden 12 Kugelzonen.

Bei der Kugel der Abbildung 9b haben alle Netzvierecke dieselbe Form. Sie sind annähernd quadratisch. Wir haben unendliche viele Breitenkreise, die sich in Richtung der Pole häufen. Damit haben wir auch unendlich viele Kugelzonen.

Bei der Kugel der Abbildung 9c haben alle Netzvierecke (inklusive die Netzdreiecke an den Polen) denselben Flächeninhalt. In unserem Beispiel ist der Flächeninhalt eines Netzviereckes der gesamten Kugeloberfläche. Die Breitenkreise bilden acht Kugelzonen.

Offenbar wird unser ästhetisches Empfinden viel mehr durch Formen als durch Flächeninhalte bestimmt.

4.3 Technische Parametrisierung

Kugel der Abbildung 9a:

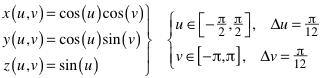(5)

Kugel der Abbildung 9b:

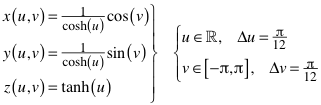(6)

Kugel der Abbildung 9c:

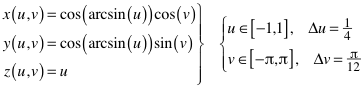(7)

Die Abbildung 10 zeigt die zugehörige Kugeldarstellung von der Seite. Wir sehen die acht gleich dicken Scheiben.

Abb. 10: Gleich dicke Scheiben

Websites

[1] Kartenprojektionen (abgerufen 13.01.2018):

http://swai.ethz.ch/swaie/MapProjector/MapProjector.de.html