Hans Walser, [20181124]

BrŸche nummerieren

Anregung: J. A., B.

1   Worum geht es?

Gesucht ist eine bijektive Abbildung zwischen den ungekŸrzten BrŸchen und den natŸrlichen Zahlen.

2   Vorgehen

Wir ordnen die ungekŸrzten BrŸche in einem Quadratraster gemŠ§ Abbildung 1a an. In einem kartesischen Koordinatensystem werden die ZŠhler horizontal und die Nenner vertikal abgetragen.

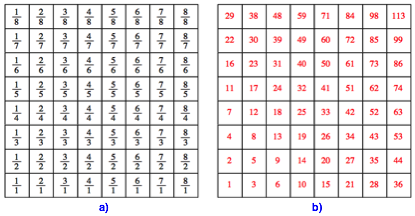
Abb. 1: Quadratraster. Wo ist die Nummer 37?

Nun nummerieren wir die Felder gemŠ§ Abbildung 1b. Damit haben wir die bijektive Zuordnung zwischen den ungekŸrzten BrŸchen und den natŸrlichen Zahlen. Jeder Bruch wird mit der Nummer im entsprechenden Feld versehen.

3   Probleme

Wie finden wir formal zu einem gegebenen Bruch seine Nummer?

Wie finden wir formal zu einer Nummer den zugehšrigen Bruch?

3.1  Vom Bruch zur Nummer

Zu einem Bruch  finden wir seine Nummer  mit folgender Prozedur.

 

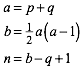                                                                                                             (1)

 

 

 

 

Hinweise zum VerstŠndnis:

a ist konstant auf einer SchrŠgzeile von links oben nach rechts unten. Das sind die SchrŠgzeilen, auf denen die Nummerierung lŠuft.

b ist die unterste Nummer in der zu a gehšrigen SchrŠgzeile.

Elimination von a und b fŸhrt auf:

 

                                                             (2)

 

 

 

Die Abbildung 2a zeigt die Niveaulinien von (2) fŸr n = 1, 2, 3, ... , 25, die Abbildung 2b die Niveaulinien fŸr n = 10, 20, 30, ... , 190.

 

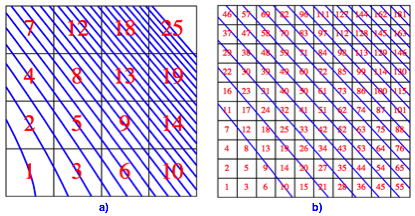
Abb. 2: Niveaulinien

Die Niveaulinien sind Kegelschnitte, da (2) quadratisch ist.

Die Abbildung 3a zeigt die zu (2) gehšrende FlŠche. In der speziellen Sicht (Abb. 3b) erkennen wir, dass die FlŠche ein parabolischer Zylinder ist. Die Niveaulinien (Abb. 2) sind SchrŠgschnitte darin, also Parabeln.

Dies kann formal eingesehen werden wie folgt.

Wir setzen:

 

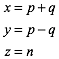                                                                                                                      (3)

 

 

 

 

Damit erhalten wir aus (2):

 

                                                                                   (4)

 

 

 

FŸr konstantes x beschreibt (4) eine Gerade (Mantellinie des Zylinders), fŸr konstantes y eine Parabel (Leitlinie des Zylinders).

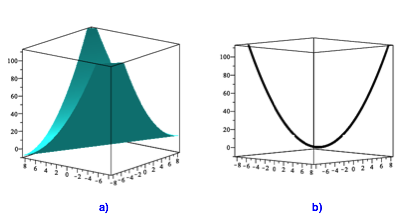
Abb. 3: FlŠche. Spezielle Sicht

3.2  Von der Nummer zum Bruch

Ausgehend von der Nummer n suchen wir ZŠhler p und Nenner q in der Form [p, q].

Die Prozedur ist folgende.

 

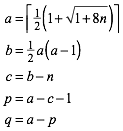                                                                                                 (5)

 

 

 

 

 

 

Bei a wird auf die nŠchste ganze Zahl aufgerundet.

a ist wiederum konstant auf einer SchrŠgzeile von links oben nach rechts unten. Das sind die SchrŠgzeilen, auf denen die Nummerierung lŠuft.

b ist die unterste Nummer in der zu a gehšrigen SchrŠgzeile.

Die Tabelle 1 gibt die ersten Werte.

 

n

[p,q]

p / q

1

[1,1]

1 / 1

2

[1,2]

1 / 2

3

[2,1]

2 / 1

4

[1,3]

1 / 3

5

[2,2]

2 / 2

6

[3,1]

3 / 1

7

[1,4]

1 / 4

8

[2,3]

2 / 3

9

[3,2]

3 / 2

10

[4,1]

4 / 1

11

[1,5]

1 / 5

12

[2,4]

2 / 4

13

[3,3]

3 / 3

14

[4,2]

4 / 2

15

[5,1]

5 / 1

Tab. 1: Erste Werte

4   GekŸrzte BrŸche

FŸr die gekŸrzten BrŸche, also die positiven rationalen Zahlen, ist die Sache weniger einfach.

Ich habe keine schšne Lšsung. Immerhin fŸhrt die AbzŠhlbarkeit der ungekŸrzten BrŸche sofort zur AbzŠhlbarkeit der gekŸrzten BrŸche. Wir haben eine Art Majorantenkriterium.

 

Websites

Hans Walser: KŸrzen

http://www.walser-h-m.ch/hans/Miniaturen/K/Kuerzen/Kuerzen.htm