Hans Walser, [20160414]

Bumerang und Affensattel

Anregung: R. S., C.

1     Worum geht es?

Es werden einige Kurven und FlŠchen mit den impliziten Darstellungen:

 

                                                           (1)

 

vorgestellt.

Dabei zeigt sich ein ParitŠtsproblem bezŸglich n.

In den meisten der folgenden Beispiele wird a = 0 gewŠhlt.

Im Raum tritt ein Affensattel auf.

Die Studie zeigt nur PhŠnomene und ist mathematisch nicht relevant.

2     Der Klassiker

FŸr n = 2 und a = 0 erhalten wir in der Ebene den Kreis mit Zentrum  und Radius  (Abb. 1)

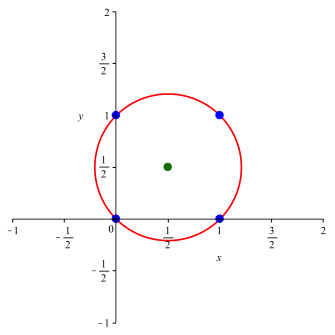
Abb. 1: Kreis

Der Kreis verlŠuft durch die vier Eckpunkte des Einheitsquadrates.

Im Raum ergibt sich die Kugel mit Zentrum  und Radius  (Abb. 2).

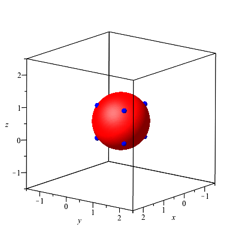
Abb. 2: Kugel

Die Kugel verlŠuft durch die acht Eckpunkte des EinheitswŸrfels.

3     Beispiele in der Ebene

Es werden einige Beispiele in der Ebene vorgestellt. Wo nichts anderes vermerkt wird, ist a = 0.

3.1    n = 1

FŸr n = 1 ergeben sich Geraden. Die Abbildung 3 zeigt die Situation fŸr a = 0.

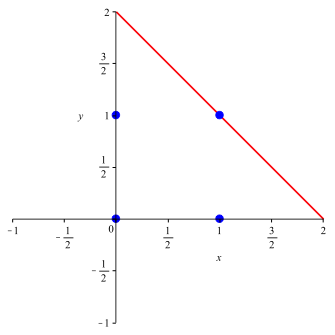
Abb. 3: n = 1, a = 0

3.2    n = 2

FŸr n = 2 ergeben sich Kreise mit dem Mittelpunkt  (Abb. 1).

3.3    n = 3

Die Abbildung 4 zeigt die Situation fŸr n = 3 und a = 0.

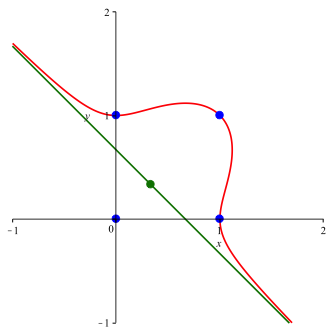
Abb. 4: n = 3, a = 0

Der Ursprung gehšrt auch zur Lšsungsmenge. Diese verlŠuft also durch die vier Eckpunkte des Einheitsquadrates. Ferner haben wir eine Asymptote, welche durch den Punkt  verlŠuft und die Steigung –1 hat.

3.4    n = 4

Die Abbildung 5 zeigt die Situation fŸr n = 4 und a = 0. Die Kurve ist geschlossen und  verlŠuft durch die vier Eckpunkte des Einheitsquadrates. Die Funktion des Punktes  ist unklar.

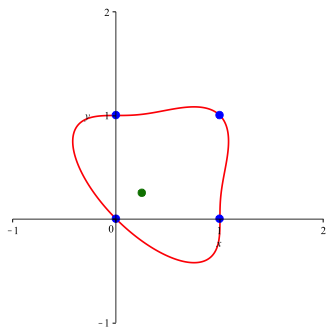
Abb. 5: n = 4, a = 0

3.5    n = 5

FŸr n = 5 (Abb. 6) ist die Situation analog wie fŸr n = 3.

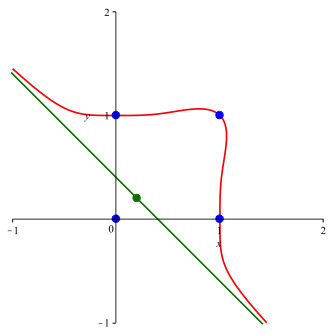
Abb. 6: n = 5, a = 0

3.6    n = 6

FŸr n = 6 (Abb. 7) ist die Situation analog wie fŸr n = 4.

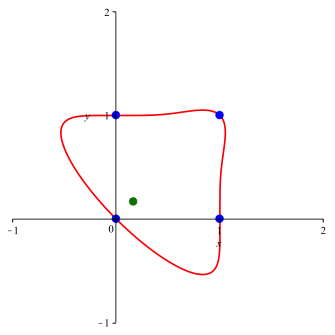
Abb. 7: n = 6, a = 0

Wir merken, wie der Hase lŠuft.

3.7    Ungerades n

Die Lšsung enthŠlt zusŠtzlich den Ursprung. Sie verlŠuft also durch die vier Eckpunkte des Einheitsquadrates. Ferner haben wir eine Asymptote, welche durch den Punkt  verlŠuft und die Steigung –1 hat.

Die Abbildungen 8 und 9 zeigen die Situation fŸr n  = 11 respektive fŸr n = 101.

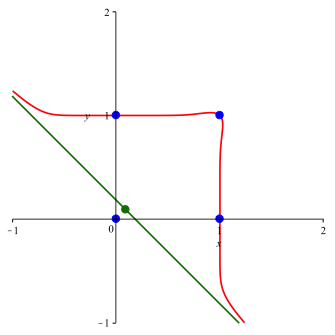
Abb. 8: n = 11, a = 0

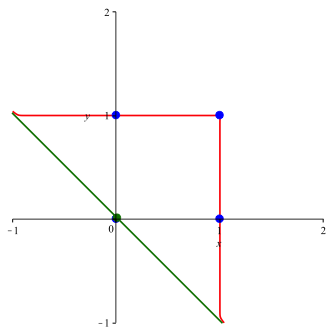
Abb. 9: n = 101, a = 0

3.8    Gerades n

Die Kurve verlŠuft durch die vier Eckpunkte des Einheitsquadrates. Die Abbildungen 10 und 11 zeigen die Situation fŸr n = 10 und n = 100.

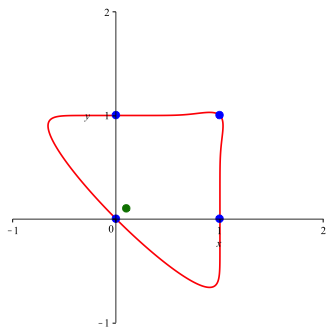
Abb. 10: n = 10, a = 0

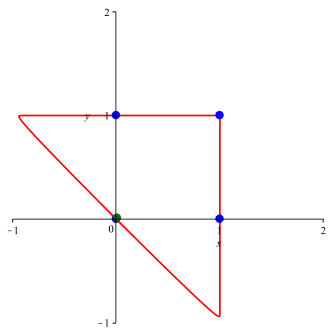
Abb. 11: n = 100, a = 0

3.9    Bumerang

FŸr n = 8 und a = –0.03 ergibt sich die Kurve der Abbildung 12. Die Kurve verlŠuft nicht mehr durch die Eckpunkte des Einheitsquadrates.

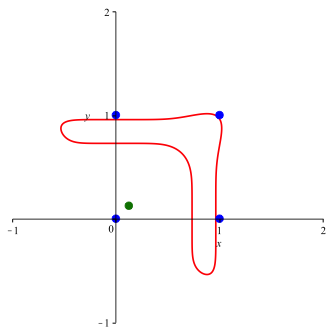
Abb. 12: Bumerang

Es wŠre jetzt allerdings falsch, von einer ãModellierungÒ eines Bumerangs zu sprechen, da wesentliche physikalische und insbesondere aerodynamische Aspekte nicht berŸcksichtigt worden sind. Der Šu§ere Schein der Form und die erste Assoziation begrŸnden keine Modellierung.  

4     Beispiele im Raum

Nun noch einige Beispiele im Raum.

4.1    n = 1 und n = 2

FŸr n = 1 ergeben sich Ebenen mit dem Normalvektor

 

                                                                                                                           (2)

 

FŸr n = 2 und a = 0 ergibt sich eine Kugel mit dem Mittelpunkt  und dem Radius  (Abb. 2). Die Kugel verlŠuft durch die acht Eckpunkte des EinheitswŸrfels.

4.2    n = 3

Die Abbildung 13 zeigt die Situation fŸr n = 3 und a = 0.

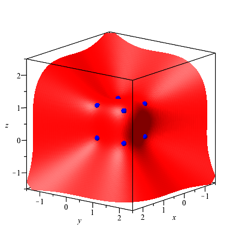
Abb. 13: n = 3, a = 0

Die FlŠche geht sichtbar durch sieben der acht Ecken des EinheitswŸrfels. Aber auch die achte Ecke (der Ursprung) ist eine Lšsung, wenn auch isoliert.

Spannend ist die Frage, was ãjanz weit au§enÒ geschieht. Aufgrund der Situation in der Ebene (Abb. 4), hat der Autor eine asymptotische Ebene erwartet. Die Abbildung 14 zeigt, was wirklich geschieht.

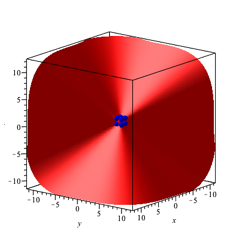
Abb. 14: Sicht aus Distanz, Affensattel

Die gewŠhlte Beleuchtung zeigt, dass wir es eher mit einem Affensattel zu tun haben. Affensattel darum, weil der Affen zusŠtzlich zu seien zwei Beinen auch den Schwanz einordnen muss. Die Abbildung 15 zeigt eine andere Sicht derselben Figur. Wir haben eine Berg- und Talbahn mit drei Bergen und drei TŠlern.

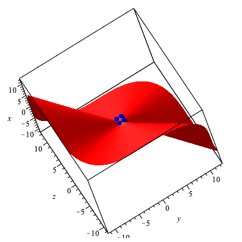
Abb. 15: Andere Sicht

Die rote FlŠche nŠhert sich nach au§en einer aus sechs ebenen FlŠchenstŸcken zusammengesetzten Grenzfigur an (Abb. 16). Die Spitzen der Sektoren haben den Punkt  gemeinsam.

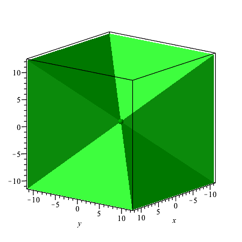
Abb. 16: GrenzflŠche

Die Abbildung 17 zeigt die Situation der Abbildung 13 zusammen mit der Grenzfigur. Die beiden Figuren durchdringen sich.

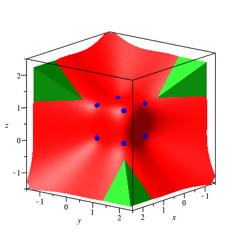
Abb. 17: Mit Grenzfigur

4.3    Die Grenzfigur fŸr ungerades n

Die Grenzfigur hat folgende Geometrie.

In einem WŸrfel wŠhlen wir sechs Kanten gemŠ§ Abbildung 18a. Zwei diametrale WŸrfelecken werden vom Kantenzug gemieden.

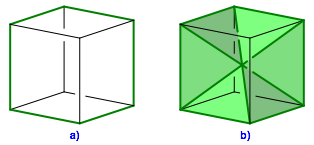
Abb. 18: Grenzfigur im WŸrfel

Vom WŸrfelmittelpunkt aus zeichnen wir nun die sechs gleichschenkligen Dreiecke mit dem WŸrfelmittelpunkt als Spitze und je einer dieser sechs WŸrfelkanten als Basis. Es entsteht ein kantiger Affensattel.

Die gleichschenkligen Dreiecke haben an der Spitze je den Winkel:

 

                                                                       (3)

 

Dieser Winkel tritt in der Kristallografie hŠufig auf.

Zwei benachbarte gleichschenklige Dreiecke haben an der gemeinsamen Kante einen Schnittwinkel von 120¡.

Diese Grenzfigur tritt in unserem Kontext bei allen ungeraden Zahlen n auf. Die Abbildung 19 zeigt die Situation fŸr n = 11.

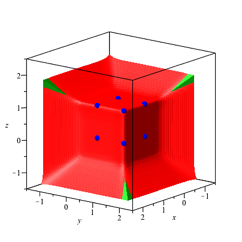
Abb. 19: n = 11, a = 0

4.4    Gerades n

Die Abbildung 20 zeigt die Situation fŸr n = 4 und a = 0.

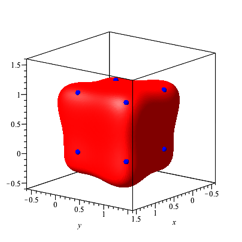
Abb. 20: n = 4, a = 0

Interessant ist natŸrlich, was an der achten Ecke des EinheitswŸrfels los ist. Dazu schauen wir die Figur von unten an und erkennen einen Affensattel (Abb. 21).

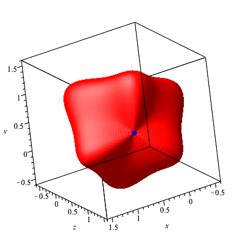
Abb. 21: Affensattel im Ursprung

Dieser Affensattel im achten Eckpunkt tritt bei allen geraden Zahlen n auf. Die Abbildungen 22 und 23 zeigen die Situation fŸr n = 10.

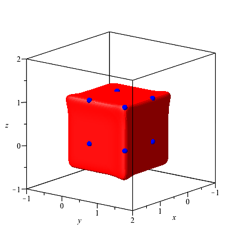
Abb. 22: n = 10, a = 0

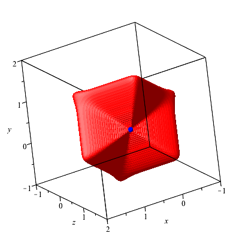
Abb. 23: n = 10, a = 0, Affensattel

4.5    Bumerang?

Die Abbildung 24 zeigt die Figur fŸr n = 8 und a = –0.03. In der Ebene erhielten wir dafŸr den Bumerang (Abb. 12).

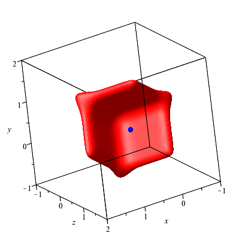
Abb. 24: Bumerang?