Hans Walser, [20230317]

Bumerang

Idee und Anregung: B. B., B. und M. S., CH.

1 Problemstellung

Die implizite Gleichung

hat für

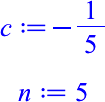
die Darstellung der Abbildung 1.

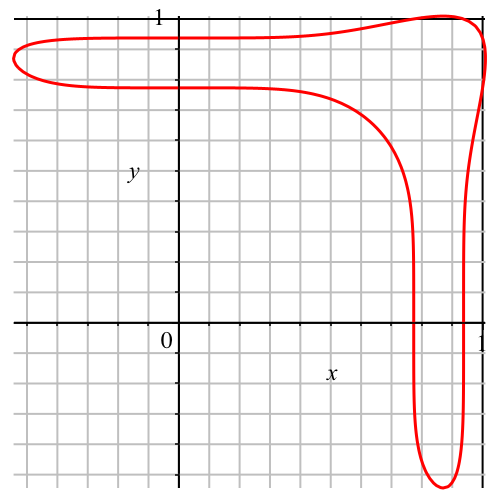
Abb. 1: Bumerang

Gesucht ist eine Polardarstellung der Kurve.

2 Verschiebung

Als Zentrum der Polardarstellung brauchen wir einen Punkt, der im Innern der Kurve liegt und von dem aus jeder Kurvenpunkt direkt angefahren werden kann, ohne vorher die Kurve zu schneiden.

Dazu eignet sich zum Beispiel der Punkt (Abb. 2) mit den Koordinaten:

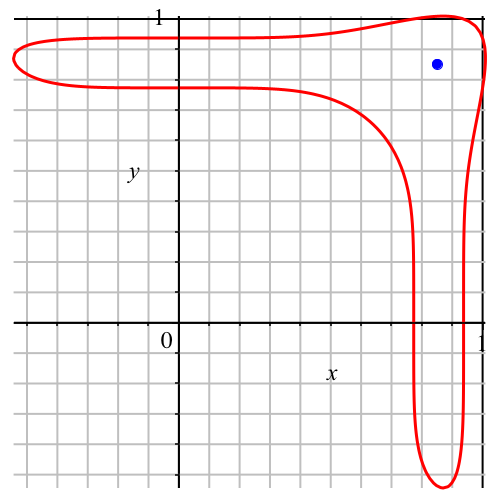
Abb. 2: Geeignetes Zentrum

Wir verschieben nun die Kurve so, dass das gewählte Zentrum in den Ursprung zu liegen kommt (Abb. 3).

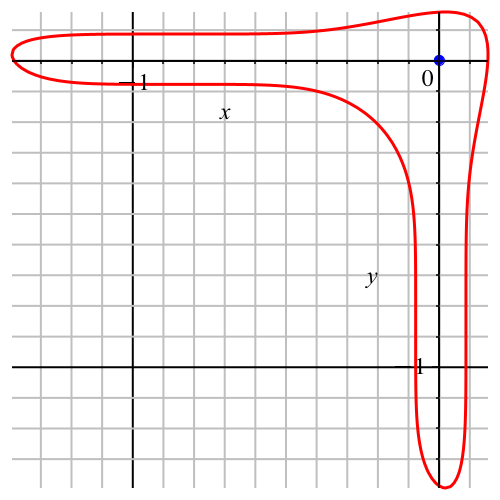
Abb. 3: Zentrum im Ursprung

Die verschobene Kurve hat die implizite Gleichung:

Zur Erinnerung: Verschieben nach links heißt Addieren vor dem Berechnen.

3 Substitution und Gleichung

Wir substituieren wie üblich:

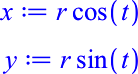
Dann lösen wir die Bedingung

nach r auf und erhalten die Polarfunktion:

Bemerkung: Das schreibt sich rasch hin, ich habe CAS mit numerischer Lösung der Gleichung verwendet.

4 Polardarstellung

Nun können wir eine Polardarstellung der Kurve bauen (Abb. 4).

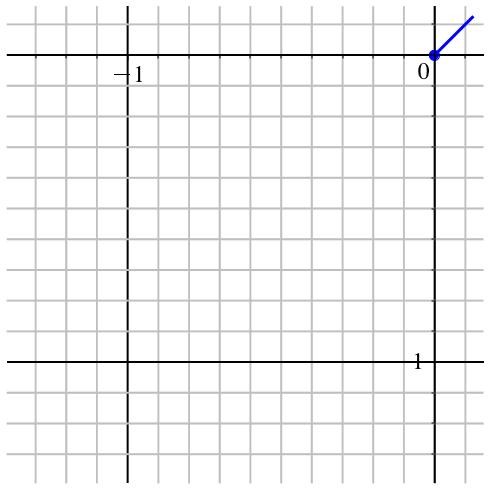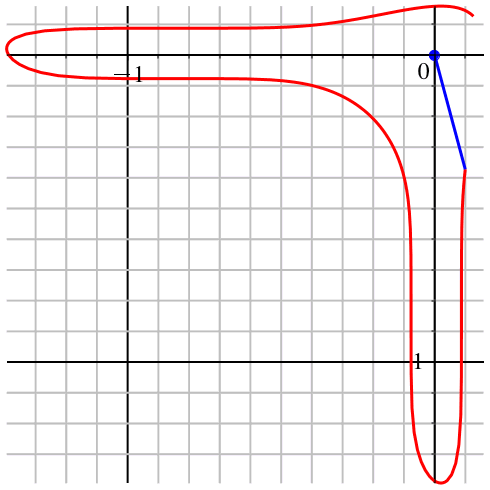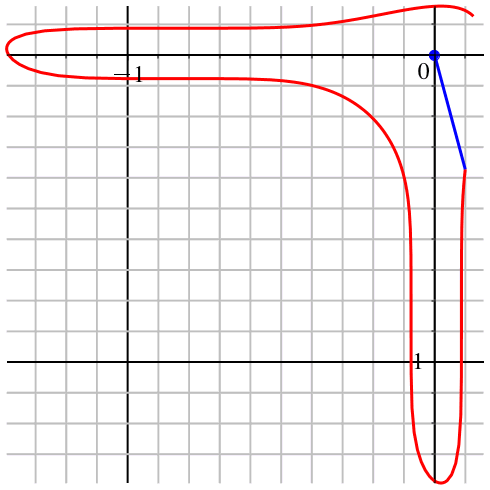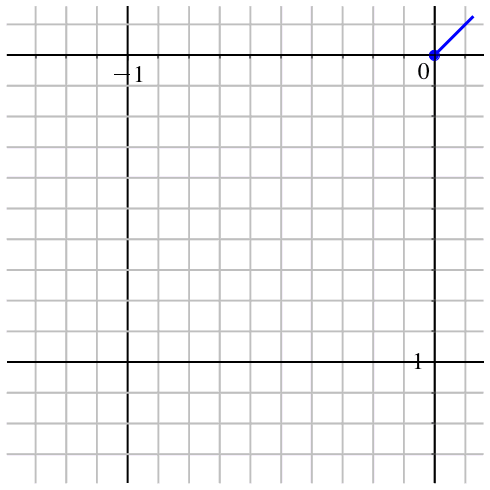
Abb. 4: Polardarstellung

Die Kurve wird mit variabler Geschwindigkeit durchlaufen. Dies liegt daran, dass der Parameter t, der Drehwinkel also, mit gleichmäßiger Geschwindigkeit dreht.

Genau genommen handelt es sich um eine Pseudo-Polardarstellung, weil für jeden Wert des Parameters t auf die implizite Gleichung zurückgegriffen wird.

Die Abbildung 5 zeigt eine Flächenvariante. Hier dreht der Drehwinkel nicht mehr gleichmäßig, um die Propellerenden schön zeichnen zu können.

Abb. 5: Flächenvariante

Weblinks

Hans Walser: Bumerang und Affensattel

http://www.walser-h-m.ch/hans/Miniaturen/B/Bumerang/Bumerang.htm

Hans Walser: Bumerang

http://www.walser-h-m.ch/hans/Miniaturen/B/Bumerang2/Bumerang2.html