Hans Walser, [20080202b]
Die Cantor-Menge im n-dimensionalen HyperwŸrfel
1
Die Cantor-Menge
Die Ÿbliche
Cantor-Menge kann generiert werden, indem wir mit den beiden Endpunkten 
und 
des Intervalls 
beginnen. Anschlie§end
wird eine Punktfolge 
mit dem
Startpunkt 
rekursiv
definiert:
Dabei ist r eine Zufallszahl aus {0, 1}. Die Punkte 
fŸhren zur
Cantor-Menge.
Die Cantor-Menge hat
die fraktale Dimension 
.
2
Im Quadrat
Im Einheitsquadrat mit
den vier Eckpunkten 
fŸhrt das
entsprechende Vorgehen zu folgendem Fraktal:
Die fraktale Dimension
ist 
, das Doppelte der fraktalen Dimension der Cantor-Menge.
3
Im WŸrfel
FŸr das entsprechende
Fraktal im WŸrfel verwenden wir die so genannte isometrische Projektion.
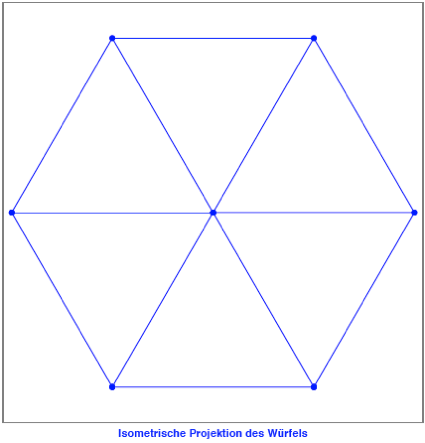
In dieser Projektion
fallen zwei diametrale WŸrfelecken in der Bildmitte aufeinander.
Das der Cantor-Menge
entsprechende Fraktal sieht nun so aus:
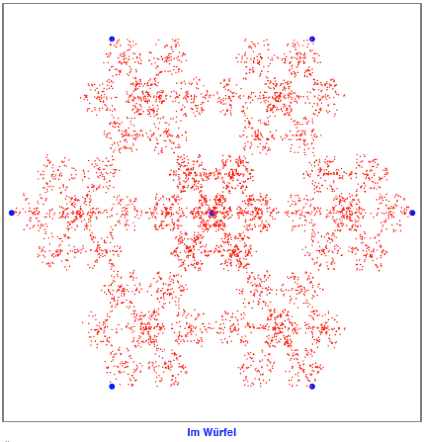
†ber die fraktale
Dimension dieses Dings kann diskutiert werden. Die Frage ist, ob das mittlere
StŸck doppelt oder einfach gezŠhlt werden soll.
Die DoppelzŠhlung
entspricht der Situation im dreidimensionalen Raum.
Wir erhalten dann die
fraktale Dimension 
, das Dreifache der fraktalen Dimension der Cantor-Menge.
Bei EinfachzŠhlung des
mittleren StŸckes ergibt sich 
.
Dieses Fraktal kann
auch mit konventionellen Methoden gebaut werden:
Die wei§en Lšcher sind
KochÕsche Schneeflocken.
4
Im vierdimensionalen Raum
Wir verwenden den
vierdimensionalen HyperwŸrfel in isometrischer Darstellung.
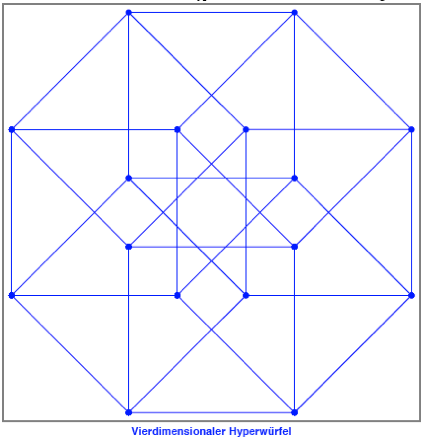
FŸr das entsprechende
Fraktal erhalten wir:
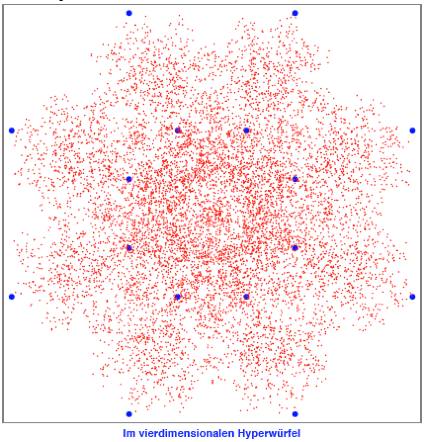
Es sind hier 10000
Punkte gezeichnet, trotzdem ist die Auflšsung nicht besonders gut.
Literatur
[Zeitler 2007] Zeitler, Herbert: DimensionsŠnderung bei der Projektion von Fraktalen. MNU, Der mathematische und naturwissenschaftliche Unterricht. 60/8, 1.12.2007, S. 464-470