Hans Walser, [20061008c]

Variationen zur Cantor-Menge

1 Entfernen des mittleren Drittels

1.1 Die klassische Cantor-Menge

Welche fraktale Dimension hat das durch die Figur angedeutete Fraktal? Dieses Fraktal heißt Cantor-Menge. In einem Intervall wird das mittlere Drittel entfernt. In den beiden verbleibenden Intervallen wird wieder das mittlere Drittel entfernt. Und so weiter.

Cantor-Menge

Bei Reduzierung auf einen Drittel erhalten wir zwei Kopien. Für die fraktale Dimension D gilt daher:

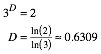
Bemerkung: Wir erhalten bei Reduzierung auf einen Drittel zwei Kopien. Das ist die Anzahl der Endpunkte der Strecke.

1.2 Quadratfrakal in der Ebene

Welche fraktale Dimension hat das durch die Figur angedeutete Fraktal? Hier wird in beiden Richtung das mittlere Drittel ausgespart.

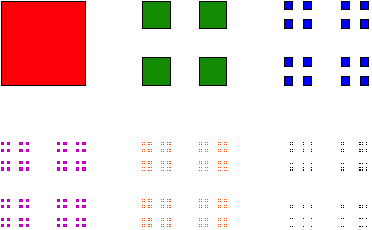
Fraktal

Bei Reduzierung auf einen Drittel erhalten wir vier Kopien. Für die fraktale Dimension D gilt daher:

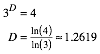
Bemerkung: Wir erhalten bei Reduzierung auf einen Drittel vier Kopien. Das ist die Anzahl der Eckpunkte des Quadrates.

1.3 Sierpinski-Teppich

Welche fraktale Dimension hat das durch die Figur angedeutete Fraktal? Dieses Fraktal heißt Sierpinski-Teppich.

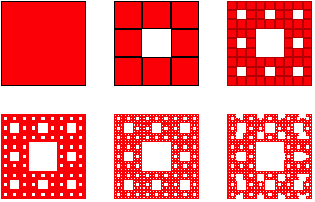
Sierpinski-Teppich

Bei Reduzierung auf einen Drittel erhalten wir acht Kopien. Für die fraktale Dimension D gilt daher:

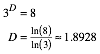
Bemerkung: Wir erhalten bei Reduzierung auf einen Drittel acht Kopien. Das ist die Summe der Anzahlen der Eckpunkte und der Kanten des Quadrates.

1.4 Würfelfraktal im Raum

Welche fraktale Dimension hat das durch die Figur angedeutete Fraktal?

Würfelfraktal

Bei Reduzierung auf einen Drittel erhalten wir acht Kopien. Für die fraktale Dimension D gilt daher:

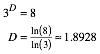
Bemerkung: Wir erhalten bei Reduzierung auf einen Drittel acht Kopien. Das ist die Anzahl der Eckpunkte des Würfels.

1.5 Menger Schwamm

Der Menger-Schwamm ist das dreidimensionale Analogon zum Sierpinski-Teppich. Bei Reduzierung auf einen Drittel erhalten wir 20 Kopien. Für die fraktale Dimension D gilt daher:

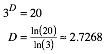
Bemerkung: Wir erhalten bei Reduzierung auf einen Drittel 20 Kopien. Das ist die Summe der Anzahlen der Eckpunkte und der Kanten des Würfels.

1.6 Das Luftkissen

Welche Fraktale Dimension hat das Fraktal, bei dem ein Interationsschritt in Grund-, Auf- und Seitenriss wie folgt dargestellt werden kann, wobei die magenta Linien nicht sichtbare Kanten darstellen. Die entstehenden Löcher sind also wie beim Emmentaler von außen nicht sichtbar; man müsste den Emmentaler aufschneiden.

Iterationsschritt

Bei Reduzierung auf einen Drittel erhalten wir 26 Kopien. Für die fraktale Dimension D gilt daher:

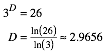
Bemerkung: Wir erhalten bei Reduzierung auf einen Drittel 26 Kopien. Das ist die Summe der Anzahlen der Eckpunkte, der Kanten und der Seitenflächen des Würfels.

2 Asymmetrisches Aussparen

In der Cantormenge wird jeweils das mittlere Drittel ausgespart. Dadurch entsteht eine symmetrische Figur. Was erhalten wir, wenn wie asymmetrisch aussparen? Welche fraktale Dimension gehört dazu?

2.1 Beispiel

Im folgenden Beispiel unterteilen wir im Verhältnis und sparen jeweils das zweite Teil aus. Damit erhalten wir eine asymmetrische Cantor-Menge.

Asymmetrische Cantor-Menge

Für die Dimension überlegen wir wie folgt. Bei Reduzierung auf einen Viertel erhalten wir drei Kopien. Für die fraktale Dimension D gilt daher:

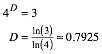
Allgemein gilt: Beim Unterteilen im Verhältnis und Weglassen des zweiten Teils erhalten wir bei Reduzierung auf insgesamt Kopien. Für die fraktale Dimension D gilt daher:

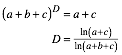
2.2 Dünner Teppich

Welche Dimension hat das durch die Figurenreihe angedeutete Fraktal?

Dünner Teppich

Bei Reduzierung auf einen Viertel erhalten wir neun Kopien. Für die fraktale Dimension D gilt daher:

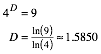
Allgemein gilt: Beim Unterteilen im Verhältnis und Beibehalten nur der Eckteile erhalten wir bei Reduzierung auf insgesamt Kopien. Für die fraktale Dimension D gilt daher:

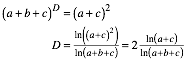
Die Dimension ist das Doppelte der Dimension der schiefen Cantor-Menge.

2.3 Asymmetrischer Sierpinski-Teppich

Welche Dimension hat das durch die Figurenreihe angedeutete Fraktal?

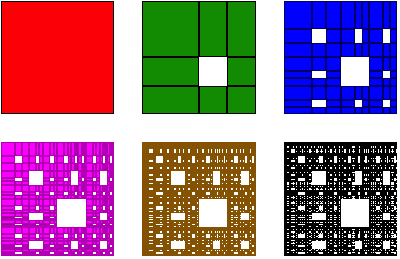
Asymmetrischer Sierpinski-Teppich

Bei Reduzierung auf einen Viertel erhalten wir 15 Kopien. Für die fraktale Dimension D gilt daher:

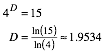
Allgemein gilt: Beim Unterteilen im Verhältnis und Weglassen des jeweils innersten Teils erhalten wir bei Reduzierung auf insgesamt

Kopien. Für die fraktale Dimension D gilt daher: