Hans Walser, [20150829]
Catalan-Zahlen
1 Problemstellung
Es sollen n Elemente auf n linear angeordnete Felder verteilt werden wie folgt. Das erste Element hat freie Platzwahl. Das zweite Element hat freie Platzwahl im ersten noch freien Intervall. Das dritte und die weiteren Elemente nacheinander freie Platzwahl im jeweils ersten freien Intervall.
Bemerkung: Ohne die Einschrnkung auf das erste freie Intervall ergben sich die n! Permutationen.
2 Codierung
Wir codieren die Reihenfolge gem§ Abbildung 1.

Abb. 1: Reihenfolge
3 Beispiele
3.1 Ein Element
Gibt nur eine Mglichkeit.
3.2 Zwei Elemente
Nun gibt es fr das erste Element zwei Mglichkeiten. Das zweite Element hat keine Wahl mehr.

Abb. 2: Zwei Elemente
In Zahlen: [1,2] und [2,1].
3.3 Drei Elemente
Wir haben fnf Mglichkeiten.
![]()
Abb. 3: Drei Elemente
In Zahlen: [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,2,1]. Hier unterscheiden sich die Anordnungsmglichkeiten von den Permutationen. Bei den Permutationen htten wir noch zustzlich [3,1,2]. Das ist in unserem Fall ausgeschlossen, weil die 2 im Intervall vor der 1 stehen muss.
3.4 Vier Elemente
Es gibt 14 Mglichkeiten.
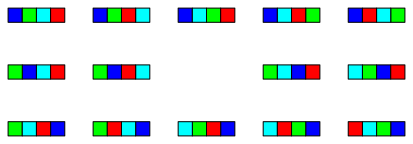
Abb. 4: Vier Elemente
Es ist 14 < 4! = 24.
3.5 Fnf Elemente
Es gibt 42 Mglichkeiten.

Abb. 5: Fnf Elemente
4 Allgemeine Formel
Wir
bezeichnen mit ![]() die Anzahl
der Anordnungen von n Elementen gem§
unseren Restriktionen.
die Anzahl
der Anordnungen von n Elementen gem§
unseren Restriktionen.
Wir
setzen ![]() , da man nur auf eine Art gar nichts tun kann.
, da man nur auf eine Art gar nichts tun kann.
Nun
nehmen wir an, das erste Element setze sich auf die Position k. Dann mssen die nachfolgenden ![]() Elemente
zwingend auf die
Elemente
zwingend auf die ![]() Pltze vor
dem ersten Element kommen. Dazu gibt es
Pltze vor
dem ersten Element kommen. Dazu gibt es ![]() Mglichkeiten. Die restlichen
Mglichkeiten. Die restlichen ![]() Elemente
kommen auf die
Elemente
kommen auf die ![]() Positionen
hinter dem ersten Element. Dazu gibt es
Positionen
hinter dem ersten Element. Dazu gibt es ![]() Mglichkeiten. Wenn das erste Element
also die Position k whlt, gibt es
insgesamt
Mglichkeiten. Wenn das erste Element
also die Position k whlt, gibt es
insgesamt ![]() Mglichkeiten.
Somit ergibt sich die Rekursion:
Mglichkeiten.
Somit ergibt sich die Rekursion:
![]() (1)
(1)
Zusammen mit dem Startwert erhalten wir:
|
n |
|
|
|
n |
|
|
0 |
1 |
|
|
|
|
|
1 |
1 |
|
|
11 |
58786 |
|
2 |
2 |
|
|
12 |
208012 |
|
3 |
5 |
|
|
13 |
742900 |
|
4 |
14 |
|
|
14 |
2674440 |
|
5 |
42 |
|
|
15 |
9694845 |
|
6 |
132 |
|
|
16 |
35357670 |
|
7 |
429 |
|
|
17 |
129644790 |
|
8 |
1430 |
|
|
18 |
477638700 |
|
9 |
4862 |
|
|
19 |
1767263190 |
|
10 |
16796 |
|
|
20 |
6564120420 |
Tab. 1: Catalan-Zahlen
Diese Zahlen sind die Catalan-Zahlen, benannt nach Eugne Charles Catalan (1814-1894). Die Catalan-Zahlen lassen sich auch berechnen mit:
![]() (2)
(2)