Hans Walser, [20230712]

Ceva

Anregung: Hans Humenberger, Wien und Jörg Meyer, Hameln

1 Worum es geht

Optimierungsproblem im Umfeld des Satzes von Ceva. Illustration

2 Sinus-Version des Satzes von Ceva

Die Sinus-Version des Satzes von Ceva besagt:

Die drei roten Ecktransversalen (Abb. 1) treffen sich genau dann in einem Punkt P, wenn:

sin(α₁) sin(β₁) sin(γ₁) = sin(α₂) sin(β₂) sin(γ₂)

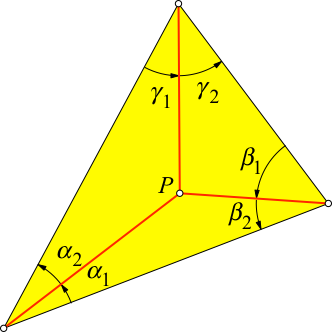
Abb. 1: Satz von Ceva

Wir untersuchen nun die Funktion (linke Seite der Ceva-Bedingung)

f(P) = sin(α₁) sin(β₁) sin(γ₁)

bei Veränderung des gemeinsamen Punktes P der drei Ecktransversalen.

3 Vorzeichen

Da wir mit orientierten Winkeln arbeiten, kann f(P) negativ werden. Es gilt:

Wenn P im Innern des Dreiecks liegt, ist f(P) > 0.

Liegt P auf einer Dreiecksseite oder der Verlängerung davon, ist f(P) = 0.

Allgemein ist f(P) > 0 für Punkte P im gelben Bereich (Abb. 2) und f(P) < 0 für Punkte P im hellblauen Bereich. Man beachte, dass sich die Ankreise des Dreiecks im negativen Bereich befinden.

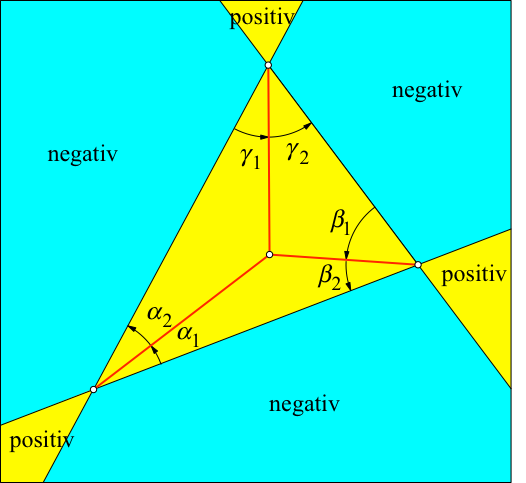
Abb. 2: Vorzeichen

4 Niveaulinien

In der Abbildung 3 sind die Niveaulinien der Funktion f(P) rot eingezeichnet. Zusätzlich sind der Inkreis und die Ankreise des Dreiecks sowie deren Mittelpunkt angegeben. Die Äquidistanz ist so normiert, dass es vom Nullniveau (Dreiecksseiten) bis zum Inkreismittelpunkt genau vier Niveauunterschiede hat.

Abb. 3: Niveaulinien

Wir vermuten, dass die Funktion f(P) in den Kreiszentren lokale Extrema annimmt, ein lokales Maximum im Inkreismittelpunkt und je ein lokales Minimum in den Ankreismittelpunkten.

In der Abbildung 4 sind die Niveaus durch Farben unterschieden.

Abb. 4: Farben

Die Abbildung 5 gibt den 3d-Funktionsgrafen. In der senkrechten Richtung ist er fünffach überhöht. Wir sehen, dass wir im Inkreismittelpunkt zwar ein lokales Maximum haben, aber außerhalb des Dreiecks (in den gelben Spickeln der Abbildung 2) noch höhere Funktionswerte. Wir sehen das auch durch Abzählen der Niveaulinien (Abb. 3) in den Außenspickeln.

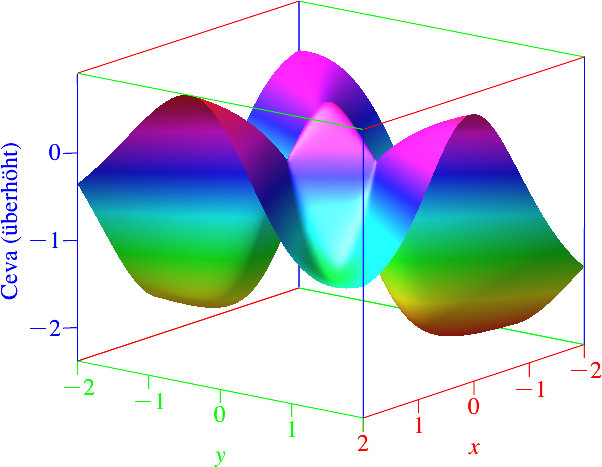
Abb. 5: Funktionsgraf

5 Gleichseitiges Dreieck

Die Abbildungen 6, 7, 8 zeigen die entsprechenden Bilder für ein gleichseitiges Dreieck. Es hat die Seitenlänge 1 und das Zentrum im Ursprung.

Abb. 6: Niveaulinien beim gleichseitigen Dreieck

Abb. 7: Farben beim gleichseitigen Dreieck

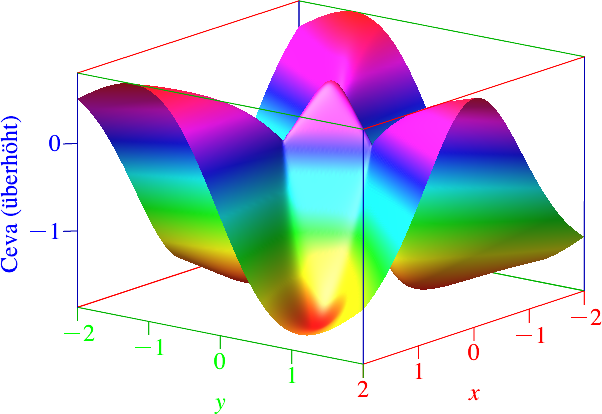
Abb. 8: Funktionsgraf beim gleichseitigen Dreieck

Abb. 9: Sicht von verschiedenen Seiten

Die Abbildung 10 zeigt einen Schnitt durch die senkrechte Symmetrale. Es deuten sich Asymptoten an. Die Zeichnung ist überhöht, aber die vertikale Skala gibt die echten Werte an. Im Inkreismittelpunkt ist f(P) = ⅛.

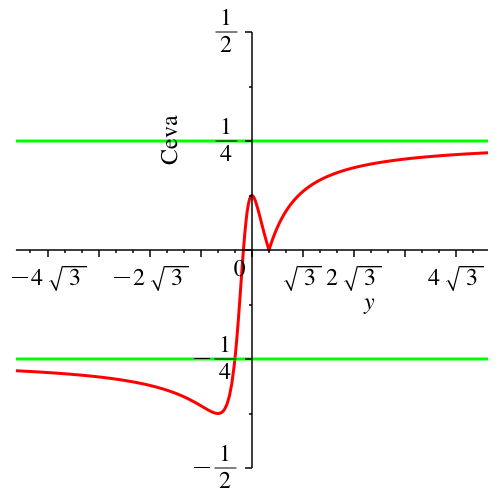
Abb. 10: Schnitt