1 Worum geht es?

Asymmetrische Konstruktion einer Ellipse im DIN-Format.

2 Konstruktion

Zu einem Kreis zeichnen wir ein orthogonales Achsenkreuz und wählen auf dem rechten horizontalen Kreuzesarm einen beliebigen Punkt (Abb. 1).

Abb. 1: Kreis, Kreuz und Punkt

In diese Figur zeichnen wir einen blauen Kreis gemäß Abbildung 2.

Abb. 2: Blauer Kreis

Weiter zeichnen wir einen grünen Kreis gemäß Abbildung 3.

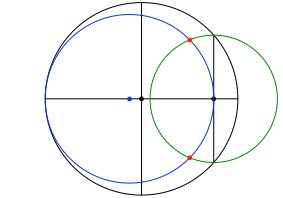
Abb. 3: Grüner Kreis

Der blaue und der grüne Kreis schneiden einander in zwei roten Punkten.

Wir fragen nach den Bahnkurven der roten Punkte, wenn der schwarze Punkt auf dem rechten Kreuzesarm variiert wird.

3 Bahnkurve

Die Abbildung 4 zeigt die Bahnkurven.

Abb. 4: Bahnkurven

Wir vermuten, dass die beiden Bahnkurven zusammen eine Ellipse bilden. Dies ist erstaunlich, da die Konstruktion bezüglich der senkrechten Kreuzlinie asymmetrisch ist, die vermutete Ellipse aber symmetrisch.

4 Beweis

Wir beweisen rechnerisch, dass die Bahnkurven tatsächlich eine Ellipse bilden.

Den Startkreis nehmen wir als Einheitskreis (Abb. 5).

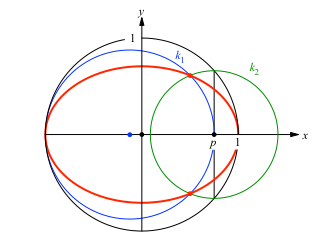
Abb. 5: Disposition

Der variable Punkt auf dem rechten Kreuzesarm habe die Koordinaten (p, 0). Für den blauen Kreis k₁ erhalten wir Mittelpunkt, Radius und Kreisgleichung wie folgt:

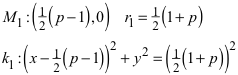
Die entsprechenden Daten für den grünen Kreis k₂ lauten:

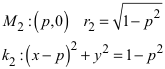
Für die Schnittpunkte der beiden Kreise erhalten wir in Abhängigkeit von p:

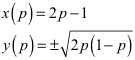
Elimination des Parameters p ergibt:

Dies ist die Gleichung einer Ellipse. Sie hat die Halbachsen:

5 Diskussion

Das Achsenverhältnis der Ellipse ist gleich dem Seitenverhältnis eines Rechteckes im DIN-Format.

Wir können der Ellipse ein diagonal gestelltes Einheitsquadrat zwischen die stumpfen Scheitel einpassen (Abb. 6).

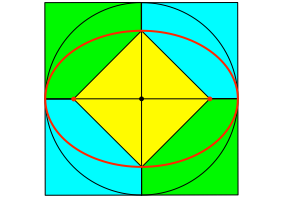
Abb. 6: Diagonal gestelltes Einheitsquadrat

Die beiden freien Quadratecken liegen in den Brennpunkten der Ellipse.

Weblink

Hans Walser: Ellipsen im DIN-Format

http://www.walser-h-m.ch/hans/Miniaturen/E/Ellipsen_DIN/Ellipsen_DIN.htm

Literatur

Walser, Hans (2013): DIN A4 in Raum und Zeit. Silbernes Rechteck – Goldenes Trapez – DIN-Quader. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-69-1.