Hans Walser, [20230821]
DIN-Format
1 Worum geht es?
Eine verallgemeinerte Fibonacci-Folge führt zum DIN-Format.
Visualisierung.
2 Die Zahlenfolge
Startwerte: a[1] := 1: a[2] := 1:
Rekursion:
a[n] := 2*a[n-1] + a[n-2]:
Bis auf den Faktor 2
ist es die gewöhnliche Fibonacci-Folge.
Die Tabelle 1 zeigt
die ersten Daten.
|
n |
a[n] |
Primfaktoren |
a[n]/ a[n-1] |
|
1 |
1 |
1 |
-1. |
|
2 |
1 |
1 |
1. |
|
3 |
3 |
Primzahl |
3. |
|
4 |
7 |
Primzahl |
2.333333333 |
|
5 |
17 |
Primzahl |
2.428571429 |
|
6 |
41 |
Primzahl |
2.411764706 |
|
7 |
99 |
3^2*11 |
2.414634146 |
|
8 |
239 |
Primzahl |
2.414141414 |
|
9 |
577 |
Primzahl |
2.414225941 |
|
10 |
1393 |
7*199 |
2.414211438 |
|
11 |
3363 |
3*19*59 |
2.414213927 |
|
12 |
8119 |
23*353 |
2.414213500 |
|
13 |
19601 |
17*1153 |
2.414213573 |
|
14 |
47321 |
79*599 |
2.414213561 |
|
15 |
114243 |
3*113*337 |
2.414213563 |
|
16 |
275807 |
7*31^2*41 |
2.414213562 |
|
17 |
665857 |
Primzahl |
2.414213562 |
|
18 |
1607521 |
103*15607 |
2.414213562 |
|
19 |
3880899 |
3^3*11*73*179 |
2.414213562 |
|
20 |
9369319 |
Primzahl |
2.414213562 |
Tab. 1: Daten
Für wachsende n
ergibt sich der Grenzwert 1 + √2 ≈ 2.4142. Damit haben wir einen ersten Link
zum DIN-Format.
3
Visualisierung
Wir beginnen mit dem
Einheitsquadrat (Abb. 1.1).

Ab. 1.1: Start
Wir setzen dem
Einheitsquadrat links und rechts ein weiteres Einheitsquadrat an (Abb. 1.2). Das
Startquadrat ist jetzt kleiner dargestellt.
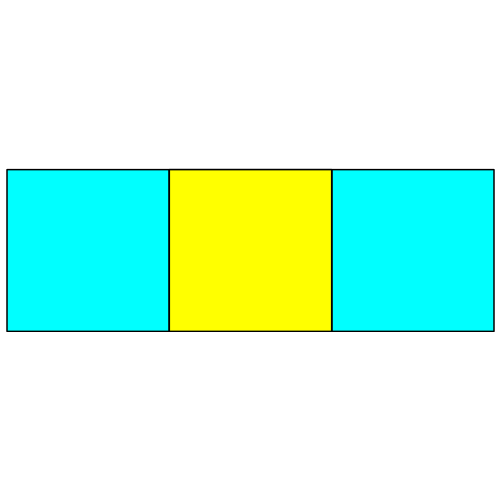
Abb.1.2: Links
und rechts
Dann setzen wir oben
und unten je ein Quadrat an. Diese haben die Seitenlängen drei (Abb. 1.3).
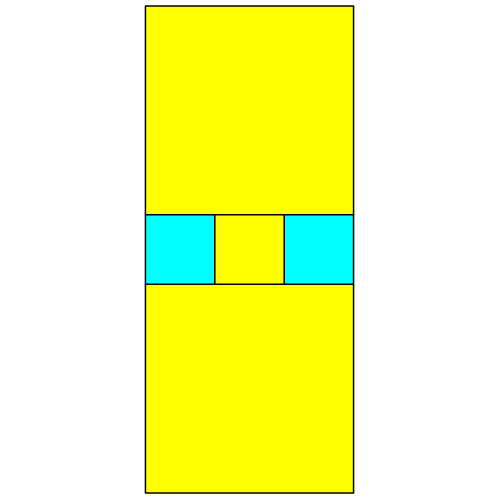
Abb. 1.3: Oben
und unten
Dann setzen wir
links und rechts je ein Quadrat an. Diese haben die Seitenlängen sieben (Abb.
1.4).
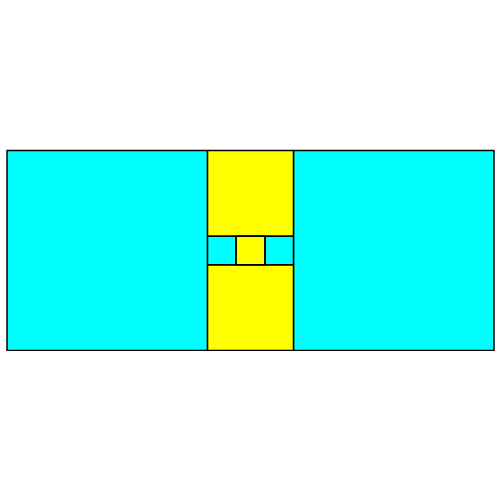
Abb. 1.4: Links
und rechts
Dann setzen wir oben
und unten je ein Quadrat an. Diese haben die Seitenlängen 17 (Abb. 1.5).
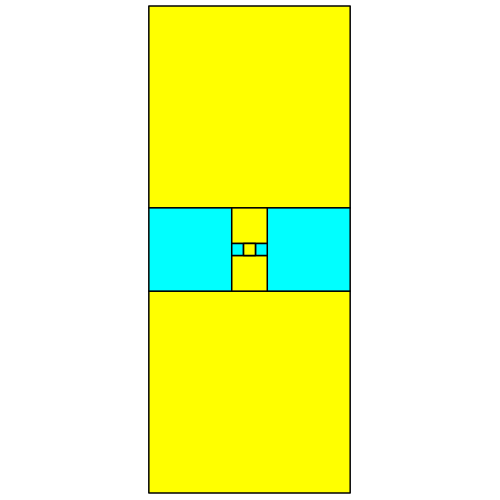
Abb. 1.5: Oben
und unten
Und so weiter. Die
Seitenlängen sind die Zahlen unserer Folge.
Die Abbildung 2
zeigt das Startquadrat in immer gleicher Größe.

Abb. 2: Schritt
für Schritt und zurück
4
Grenzrechteck
Die Rechtecke
approximieren ein Rechteck mit dem Seitenverhältnis (1 + √2):1.
Dieses Rechteck
können wir auf zwei Arten aus dem DIN-Rechteck (das DIN-Rechteck hat das
Seitenverhältnis √2:1) erhalten.
4.1 Absetzen
Wir setzen dem
DIN-Rechteck ein Quadrat an (Abb. 3).

Abb. 3: Quadrat
ansetzen
4.2 Abschneiden
Wir schneiden vom
DIN-Rechteck ein Quadrat ab (Abb. 4).

Abb. 4:
Abschneiden
4.3 Diagonalen
Die Diagonalen des
Rechtecks schneiden sich unter 45° (Abb.5).
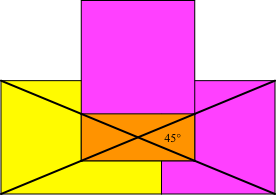
Abb. 5:
Diagonalen
Die Figur lässt sich
in ein regelmäßiges Achteck einpassen.
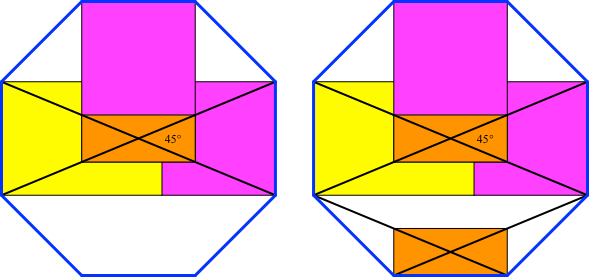
Abb. 6: Achteck
Weblink
Hans Walser: Miniaturen: DIN-Format
http://www.walser-h-m.ch/hans/Miniaturen_Uebersicht/DIN_Format/index.html