Hans Walser, [20111021a]
DIN-Format und Goldener Schnitt
1 Zwei Kreisbšgen
1.1
Konstruktion
Wir konstruieren die
Winkelhalbierende eines Winkels und halbieren die anschlie§enden Rechtecksseiten
(Abb. 1). Beides kann mit Falten geschehen.
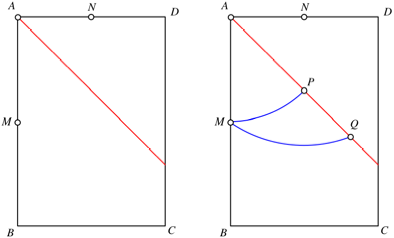
Abb. 1: Zwei Kreisbšgen
Nun zeichnen wir einen
Kreisbogen um A durch M und einen Kreisbogen um N durch M.
Diese Kreisbšgen schneiden die Winkelhalbierende in P beziehungsweise Q.
Die Abschnitte 
und 
stehen im
VerhŠltnis des goldenen Schnittes.
1.2
Beweis
Wir normieren die
Strecke 
auf 1. Damit
gelten die in der Abbildung 2 eingezeichneten LŠngen.
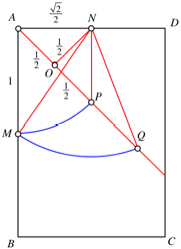
Abb. 2: Beweisfigur
Weiter ist:
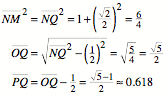
Dies ist der Goldene
Schnitt, vgl. [Walser 2009].
2
Kombination von DIN A4 und DIN A6
Wir beginnen mit einem
DIN A4 Blatt und Falten eine Winkelhalbierende und die lange Mittelparallele
(Abb. 30). P sei der Schnittpunkt der
beiden Faltlinien.
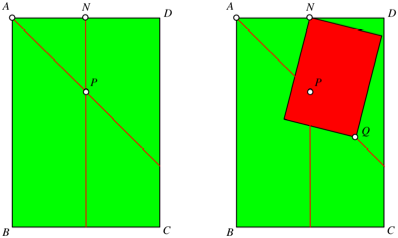
Abb. 3: DIN A4 und DIN
A6
Anschlie§end passen wir
eine DIN A6 Karte ein gemŠ§ Abbildung 3.
Die Abschnitte 
und 
stehen im
VerhŠltnis des goldenen Schnittes.
Der Beweis ergibt sich
als Variante des ersten Beispiels.
3
Goldenes Rechteck
Durch Erweiterung der
ersten Konstruktion gelangen wir zum Goldenen Rechteck (Abb. 4).
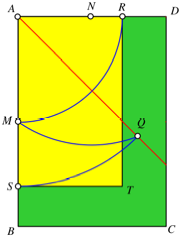
Abb. 4: Goldenes
Rechteck
Literatur
[Walser 2009] Walser,
Hans: Der Goldene Schnitt. 5., bearbeitete und erweiterte Auflage. Mit einem
Beitrag von Hans Wu§ing źber populŠrwissenschaftliche Mathematikliteratur aus
Leipzig. Edition am Gutenbergplatz, Leipzig 2009. ISBN 978-3-937219-98-1