Hans Walser, [20230809]
DIN-Format und Goldener Schnitt
1 Worum es geht
Link zwischen dem DIN-Format und dem Goldenen Schnitt
2 Konstruktion
Den Katheten eines rechtwinkligen Dreieckes setzen wir Rechtecke im DIN-Format, also mit dem Seitenverhältnis √2:1, auf der Schmalseite an (Abb. 1).
Anschließend zeichnen wir zwei Kreise. Deren Zentren sind die Eckpunkte mit den spitzen Winkeln des rechtwinkligen Dreiecks, und die Radien die Diagonalen des jeweiligen angesetzten DIN-Rechteckes.
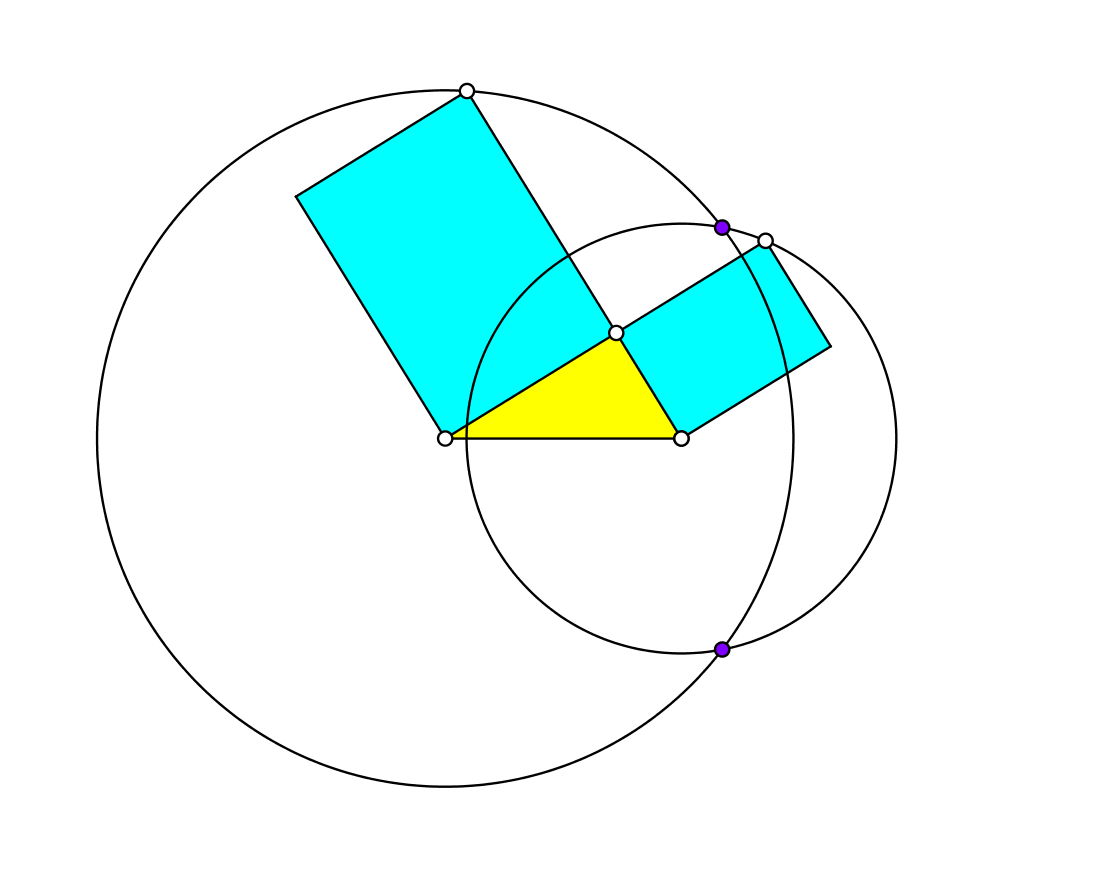
Abb. 1: Konstruktion
In der Situation der Abbildung 1 haben die beiden Kreise zwei Schnittpunkte.
Wie ändert sich das Schnittpunktverhalten bei Veränderung des rechtwinkligen Dreieckes (Abb. 2)?
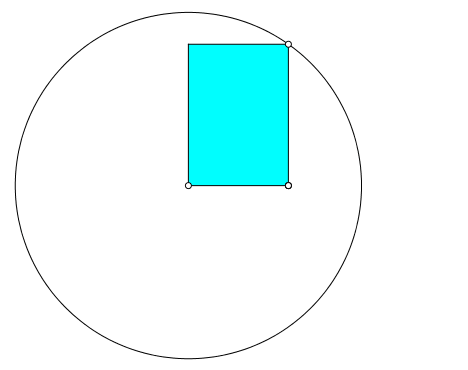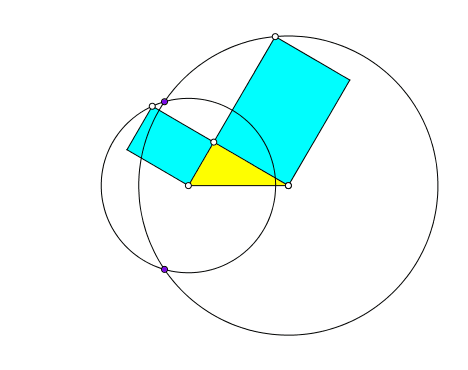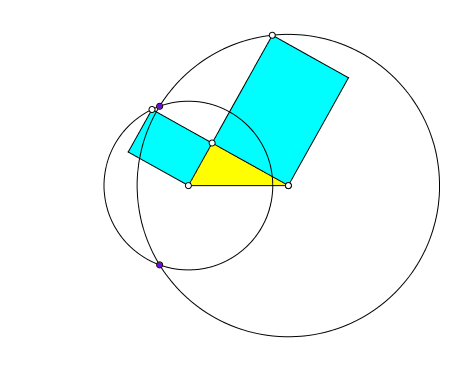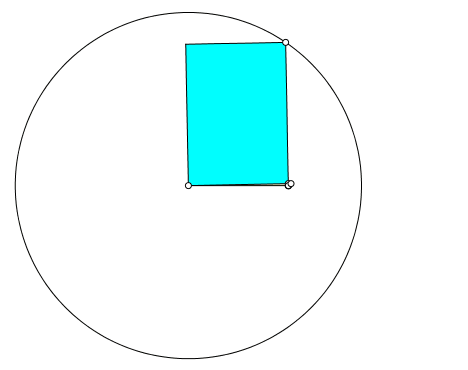
Abb. 2: Variation des rechtwinkligen Dreieckes
3 Spezielle Situationen
3.1 Berührung links
Die Abbildung 3 zeigt die Situation, in der sich die beiden Kreise links berühren. Das zu einem Rechteck ergänzte rechtwinklige Dreieck ist ein Hochgoldenes Rechteck mit dem Seitenverhältnis Φ2:1. Dabei ist Φ = (1+√5)/2 ≈ 1.618 der Goldene Schnitt. Die Radien der beiden Kreise verhalten sich ebenfalls wie Φ2:1. Der Goldene Schnitt erscheint in den mit Major (rot) und Minor (blau) markierten Strecken.
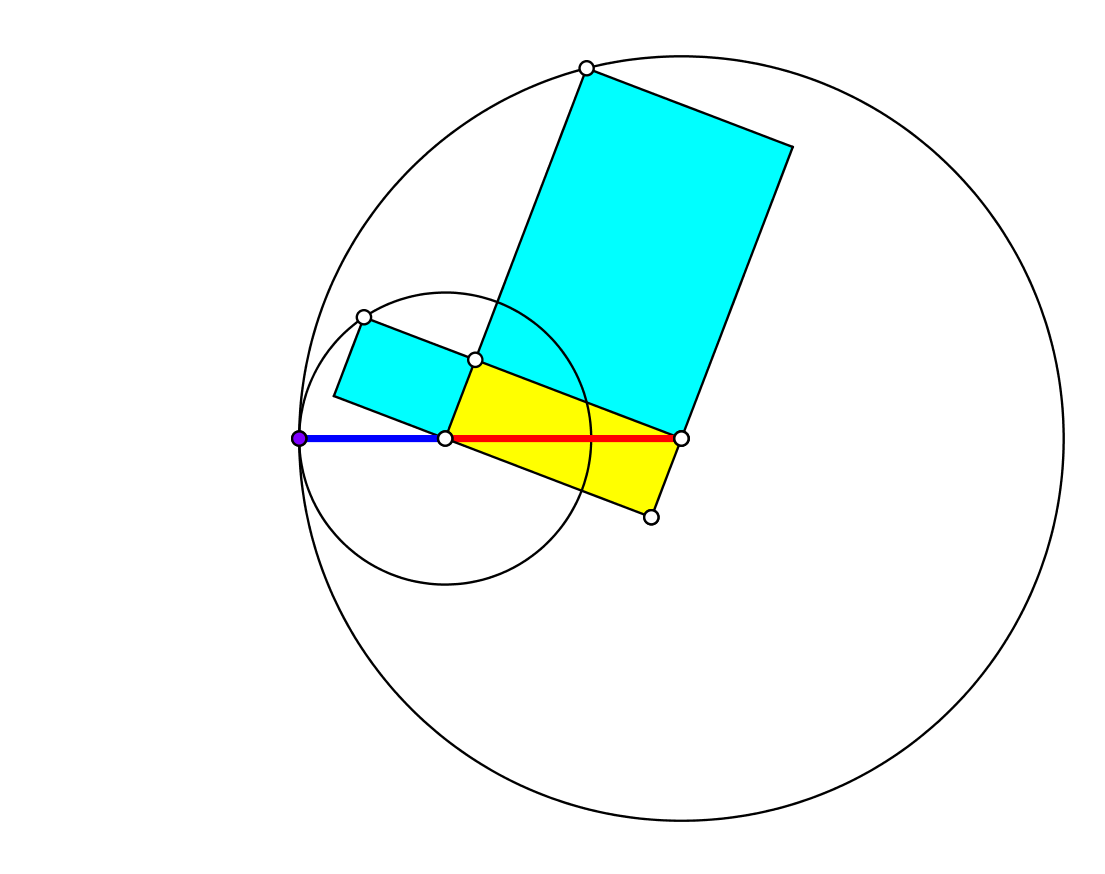
Abb. 3: Berührung links
3.2 Symmetrische Situation
Die Abbildung 4 zeigt die symmetrische Situation mit einem rechtwinklig gleichschenkligen Dreieck. Der Goldene Schnitt erscheint in den mit Major (rot) und Minor (blau) markierten Strecken.
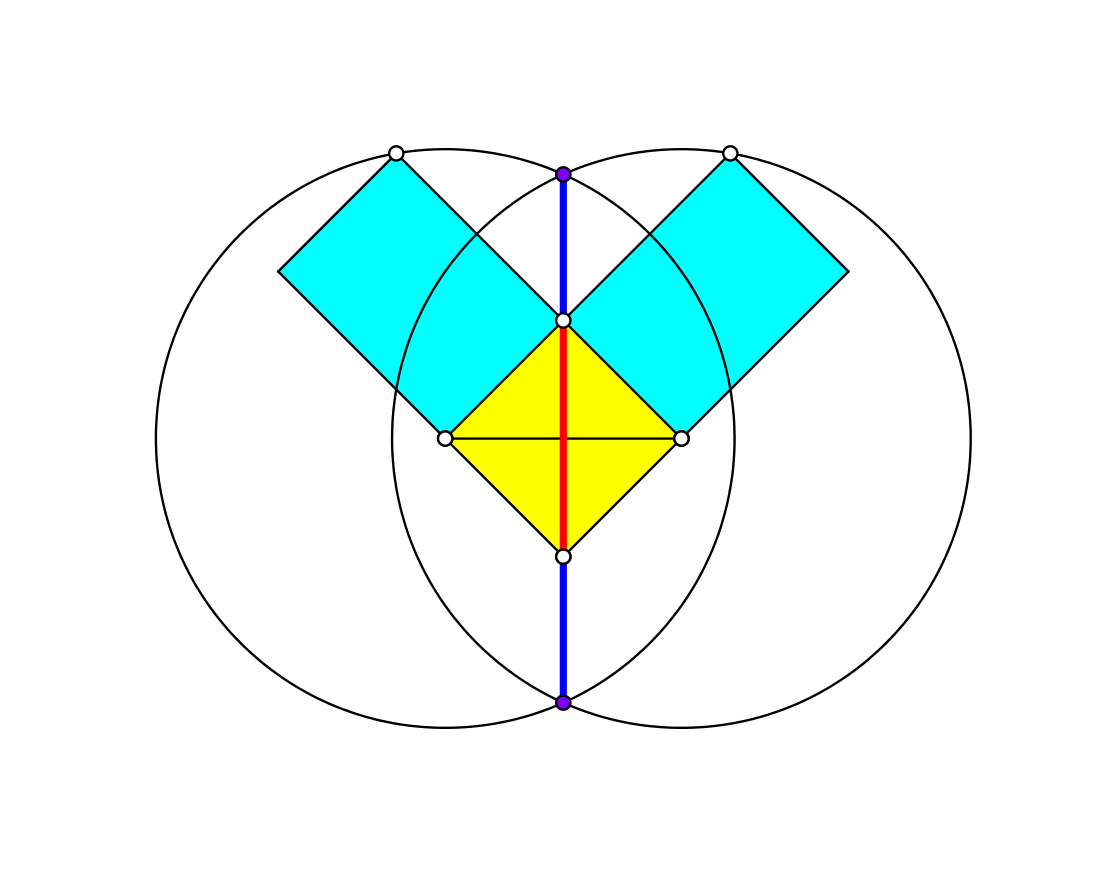
Abb. 4: Symmetrische Situation
3.3 Berührung rechts
Die Berührung rechts (Abb. 5) ist spiegelbildlich zur Berührung links (Abb. 3).
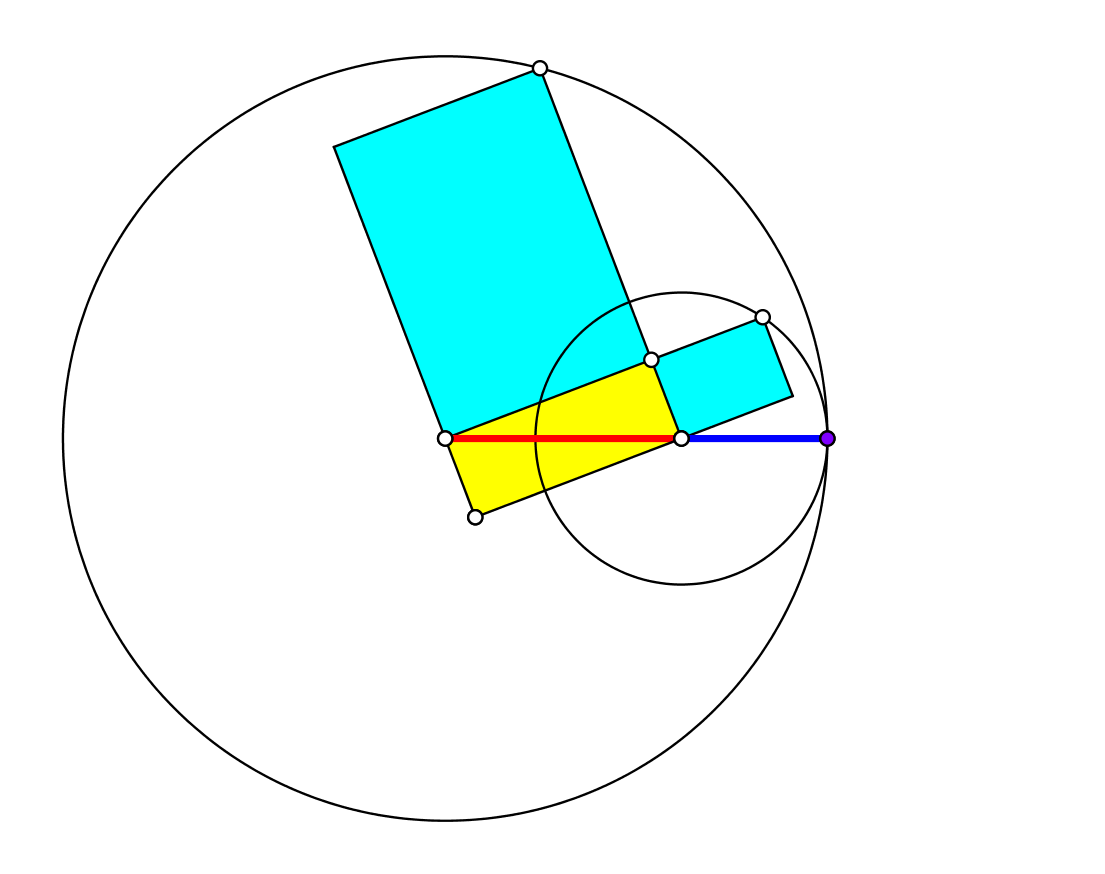
Abb. 5: Berührung rechts
4 Allgemeine Situation
Die beiden Schnittpunkte liegen, sofern sie existieren, auf einem Kreis, der sich mit dem Goldenen Schnitt in der Figur verorten lässt (Abb. 6).
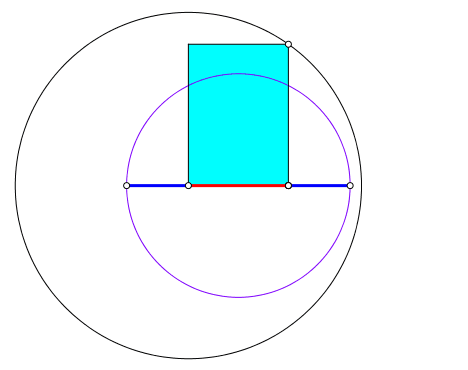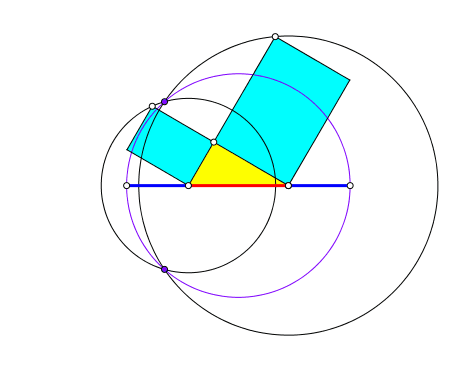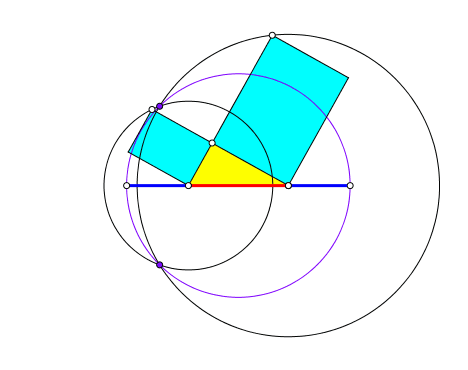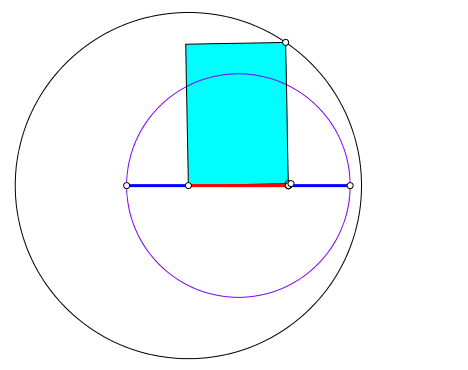
Abb. 6: Schnittpunkte auf Kreis
Weblinks
Hans Walser: DIN-Format und Goldener Schnitt
Hans Walser: DIN-Format und Goldener Schnitt
http://www.walser-h-m.ch/hans/Miniaturen/D/DIN_Goldener_Schnitt/DIN_Goldener_Schnitt.htm
Hans Walser: DIN-Format und Goldener Schnitt
Hans Walser: DIN-Format, Goldener Schnitt und gleichseitiges Dreieck
http://www.walser-h-m.ch/hans/Miniaturen/D/DIN-Format3/DIN-Format3.htm