Hans Walser, [20111224a]
DIN-Formate
1
Verschiedene DIN-Formate
Wir legen einen Rechtecksraster aus DIN A4 Blttern aus. Ein kleines Rasterrechteck hat also das DIN A4-Format.
Welches DIN-Format
haben dann die folgenden roten Rechtecke?
a) 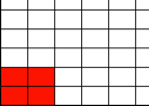 b)
b) 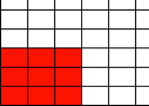
c) 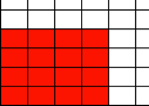 d)
d) 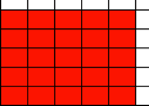
Welches DIN-Format haben
die roten Rechtecke?
Bearbeitung
Das DIN A-System ist
ein Flchensystem. DIN A0 hat den Flcheninhalt 1 m2, jede weitere
DIN A-Nummer halbiert den Flcheninhalt. Ein DIN A4 – Rechteck hat also
den Flcheninhalt ![]() (die Ma§einheit
m2 wird im folgenden weggelassen).
(die Ma§einheit
m2 wird im folgenden weggelassen).
Allgemein ist ![]() der
Flcheninhalt eines Rechtecks im DIN A-System.
der
Flcheninhalt eines Rechtecks im DIN A-System.
Die roten Rechtecke
haben alle das fr das DIN A-Format typische Seitenverhltnis ![]() , es passen aber nicht alle in das ganzzahlige DIN A-System.
, es passen aber nicht alle in das ganzzahlige DIN A-System.
Fr die einzelnen
Beispiele erhalten wir:
a) Der Flcheninhalt
ist vier Mal so gro§ wie beim DIN A4-Rechteck, also ![]() . Somit haben wir es mit einem DIN A2-Rechteck zu tun.
. Somit haben wir es mit einem DIN A2-Rechteck zu tun.
b) Der Flcheninhalt
ist ![]() . Gesucht ist nun x
so, dass
. Gesucht ist nun x
so, dass ![]() . Wir erhalten also eine Exponentialgleichung. Die Lsung ist
. Wir erhalten also eine Exponentialgleichung. Die Lsung ist
![]() . Das rote Rechteck hat also das Format DIN A0.8301. Zwischen
a) und b) msste eigentlich das Rechteck DIN A1 liegen. Wo ist das geblieben?
. Das rote Rechteck hat also das Format DIN A0.8301. Zwischen
a) und b) msste eigentlich das Rechteck DIN A1 liegen. Wo ist das geblieben?
c) Wir haben analog: ![]() . Also DIN A0. Htte man auch ohne Rechnung merken knnen.
. Also DIN A0. Htte man auch ohne Rechnung merken knnen.
d) ![]() . Wir erhalten eine negative DIN A-Nummer. Das ist jetzt fr
alle Rechtecke mit dem Seitenverhltnis
. Wir erhalten eine negative DIN A-Nummer. Das ist jetzt fr
alle Rechtecke mit dem Seitenverhltnis ![]() so, welche
gr§er sind als das DIN A0-Rechteck.
so, welche
gr§er sind als das DIN A0-Rechteck.
2
Rechnen in DIN-Formaten
2.1
Addition
Wir addieren die
Flchen von zwei DIN-Formaten und mchten das wieder als DIN-Format ausdrcken.
Geometrisch also eine Flchenverwandlungsaufgabe. Rechnerisch sieht das Problem
so aus: Zu gegebenen x und y ist z
so gesucht, dass flchenm§ig gilt:
![]()
Das Problem lst sich
mit Pythagoras illustrieren.
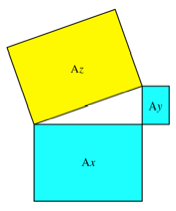
Illustration mit
Pythagoras
Bearbeitung
Es muss gelten:
![]()
Damit wird:
![]()
Mit dem Logarithmus zur
Basis 2 (dualer Logarithmus, ![]() ) lsst sich das etwas einfacher schreiben:
) lsst sich das etwas einfacher schreiben:
![]()
Beispiel 1: ![]() . Wir erhalten:
. Wir erhalten:
![]()
Das htte man auch
einfacher haben knnen.
Beispiel 2: ![]() . Wir erhalten:
. Wir erhalten:
![]()
2.2
Skalare Multiplikation
Wir multiplizieren die
Flche eines DIN-Formates mit der Zahl ![]() und mchten das
wieder als DIN-Format ausdrcken. Also: Zu gegebenen x und
und mchten das
wieder als DIN-Format ausdrcken. Also: Zu gegebenen x und ![]() ist z so gesucht, dass flchenm§ig gilt:
ist z so gesucht, dass flchenm§ig gilt:
![]()
Es muss also gelten:
![]()
Damit wird:
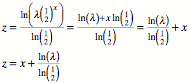
Man beachte: Fr ![]() wird
wird ![]() .
.
Mit dem Logarithmus zur
Basis 2 sieht das so aus:
![]()
Beispiel: Fr ![]() (Verdoppeln der
Flche) reduziert sich die DIN A-Nummer um 1.
(Verdoppeln der
Flche) reduziert sich die DIN A-Nummer um 1.