Hans Walser, [20120822]
DIN-Quader
1 Quader halbieren
Ein Quader soll durch eine Mittelparallelebene volumenmŠ§ig so halbiert werden, dass die beiden Teilquader kongruent und zum Ausgangsquader Šhnlich sind.
Bearbeitung
Der Ausgangsquader habe
die KantenlŠngen a, b und c mit 
und der Normierung
. Ein Teilquader hat wegen der geforderten €hnlichkeit die
KantenlŠngen 
, 
und 
. Die Volumenbedingung liefert
Da die lŠngste Kante
halbiert c zur kŸrzesten Kante 
wird, haben wir
Die mittlere Kante b wird zur lŠngsten Kante 
, also ist
Der Ausgangsquader hat
also die KantenlŠngen 
, 
, 
. Unter Weglassung der Normierung 
ergibt sich das
KantenverhŠltnis
Die drei KantenlŠngen bilden eine geometrische Folge. Die mittlere Kante ist das geometrische Mittel der kŸrzesten und der lŠngsten Kante.
Numerische Werte:
Die SchlŸsselgrš§e 
lŠsst sich nicht
mit Zirkel und Lineal konstruieren (Delisches Problem).
Die Abbildung 1 zeigt die Abwicklung eines solchen Quaders.
Abb. 1: Abwicklung
Die Abbildung 2 zeigt die fŸr ein Flechtmodell benštigten drei Streifen.
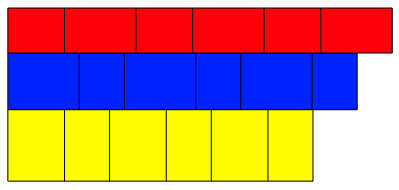
Abb. 2: Die drei Streifen fŸr das Flechtmodell
Die Abbildung 3 zeigt Flechtmodelle aus drei Streifen.
Abb. 3: Flechtmodelle aus drei Streifen
Die Abbildung 4 zeigt den DIN-Quader in isometrischer Darstellung mit dem EinheitswŸrfel zu Vergleich.
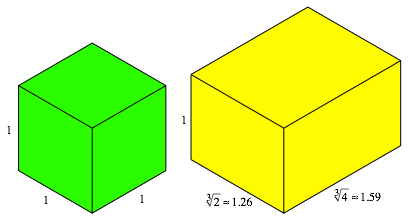
Abb. 4: WŸrfel und DIN-Quader
2 Quader vierteln
Ein Quader soll durch zwei Mittelparallelebenen volumenmŠ§ig so geviertelt werden, dass die vier Teilquader kongruent und zum Ausgangsquader Šhnlich sind.
Bearbeitung
Der Ausgangsquader hat ebenfalls das KantenverhŠltnis
.
Zwei Mal halbiert ist gut geviertelt.
3 Quader achteln
Ein Quader soll durch drei Mittelparallelebenen volumenmŠ§ig so geachtelt werden, dass die acht Teilquader kongruent und zum Ausgangsquader Šhnlich sind.
Bearbeitung
Geht mit jedem Quader.
4 4d-Quader
a) Ein 4d-Quader soll durch eine Mittelparallelebene volumenmŠ§ig so halbiert werden, dass die beiden 4d-Teilquader kongruent und zum Ausgangs-4d-Quader Šhnlich sind.
b) Ein 4d-Quader soll durch zwei Mittelparallelebenen volumenmŠ§ig so geviertelt werden, dass die vier 4d-Teilquader kongruent und zum Ausgangs-4d-Quader Šhnlich sind.
c) Ein 4d-Quader soll durch drei Mittelparallelebenen volumenmŠ§ig so geachtelt werden, dass die acht 4d-Teilquader kongruent und zum Ausgangs-4d-Quader Šhnlich sind.
Bearbeitung
Der Ausgangs-4d-Quader hat in allen drei FŠllen das KantenverhŠltnis
.
5 n-d-Quader.
5.1 Anschluss an ein metrisches System
Analog zur DIN-A-Reihe suchen wir in der Dimension n eine Reihe von Quadern Qk, so dass wir durch Halbieren von Qk auf Qk+1 kommen. Zudem soll Q0 das n-d-Volumen 1 haben. Die n KantenlŠngen des Quaders Qk bezeichnen wir mit
.
FŸr den
LŠngenverkŸrzungsfaktor f haben wir 
. Damit ist:
5.2 Beispiele
Im Folgenden einige Beispiele.
5.2.1 Dimension 1
Wir haben den
Verkleinerungsfaktor 
. Tabelle:
|
Q0 |
1.0 |
|
Q1 |
0.5 |
|
Q2 |
0.25 |
|
Q3 |
0.125 |
|
Q4 |
0.0625 |
|
Q5 |
0.03125 |
|
Q6 |
0.015625 |
|
Q7 |
0.0078125 |
|
Q8 |
0.0039062 |
|
Q9 |
0.0019531 |
|
Q10 |
0.00097656 |
|
Q11 |
0.00048828 |
|
Q12 |
0.00024414 |
|
Q13 |
0.00012207 |
|
Q14 |
0.000061035 |
|
Q15 |
0.000030518 |
Die EinheitslŠnge wird sukzessive halbiert. Alle Zahlen sind rational.
5.2.2 Dimension 2
Wir haben den
Verkleinerungsfaktor 
. Wir erhalten die Ÿbliche A-Tabelle.
|
A0 |
0.8409 *
1.1892 |
|
A1 |
0.5946 *
0.8409 |
|
A2 |
0.42045 *
0.5946 |
|
A3 |
0.2973 *
0.42045 |
|
A4 |
0.21022 *
0.2973 |
|
A5 |
0.14865 *
0.21022 |
|
A6 |
0.10511 *
0.14865 |
|
A7 |
0.074325 *
0.10511 |
|
A8 |
0.052556 *
0.074325 |
|
A9 |
0.037163 *
0.052556 |
|
A10 |
0.026278 *
0.037163 |
|
A11 |
0.018581 *
0.026278 |
|
A12 |
0.013139 *
0.018581 |
|
A13 |
0.0092907 *
0.013139 |
|
A14 |
0.0065695 *
0.0092907 |
|
A15 |
0.0046453 *
0.0065695 |
Alle TabelleneintrŠge sind irrational.
Die Abbildung 5 zeigt die Ÿbliche Aufgliederung. Das Umrissrechteck hat das Format A0.
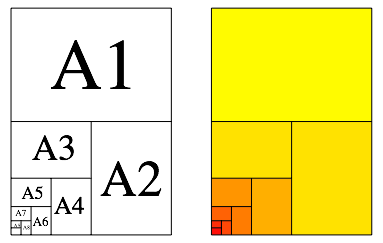
Abb. 5: Aufgliederung
5.2.3 Dimension 3
Wir haben den
Verkleinerungsfaktor 
. Tabelle:
|
Q0 |
0.7937 * 1 * 1.2599 |
|
Q1 |
0.62996 * 0.7937 * 1 |
|
Q2 |
0.5 * 0.62996 * 0.7937 |
|
Q3 |
0.39685 * 0.5 * 0.62996 |
|
Q4 |
0.31498 * 0.39685 * 0.5 |
|
Q5 |
0.25 * 0.31498 * 0.39685 |
|
Q6 |
0.19843 * 0.25 * 0.31498 |
|
Q7 |
0.15749 * 0.19843 * 0.25 |
|
Q8 |
0.125 * 0.15749 * 0.19843 |
|
Q9 |
0.099213 * 0.125 * 0.15749 |
|
Q10 |
0.078745 * 0.099213 * 0.125 |
|
Q11 |
0.0625 * 0.078745 * 0.099213 |
|
Q12 |
0.049606 * 0.0625 * 0.078745 |
|
Q13 |
0.039373 * 0.049606 * 0.0625 |
|
Q14 |
0.03125 * 0.039373 * 0.049606 |
|
Q15 |
0.024803 * 0.03125 * 0.039373 |
Wir haben bei Q0 die
mittlere KantenlŠnge 1. In jedem Quader ist eine KantenlŠnge rational. Der
Faktor 
lŠsst sich aber
nicht mit Zirkel und Lineal konstruieren (Delisches Problem).
Die Abbildungsfolge 6 zeigt die Aufgliederung von Q1, Q2, Q3, ... , Q12.
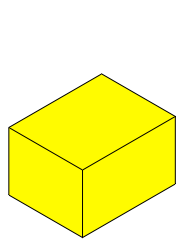
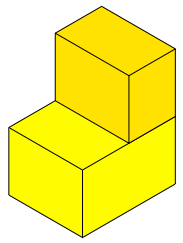
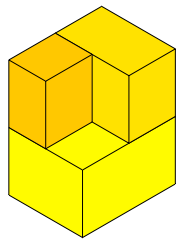
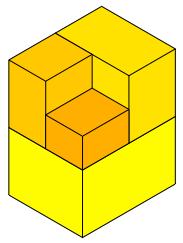
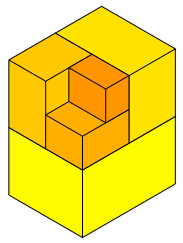
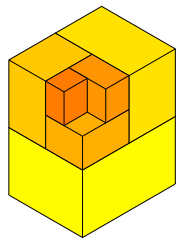
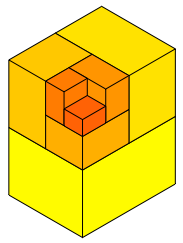
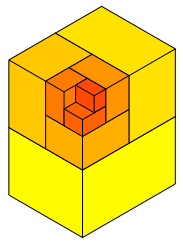
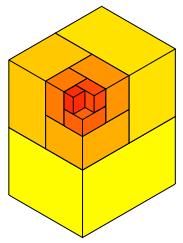
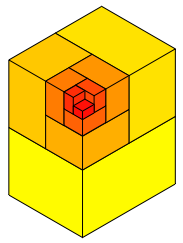
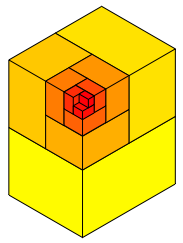
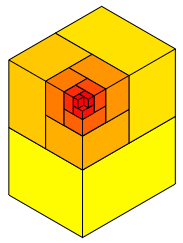
Abb. 6.1: Q1 bis Q12
Die Grenzfigur ist Q0.
5.2.4 Dimension 4
Wir haben den
Verkleinerungsfaktor 
. Tabelle:
|
Q0 |
0.77111 * 0.917 * 1.0905 * 1.2968 |
|
Q1 |
0.64842 * 0.77111 * 0.917 * 1.0905 |
|
Q2 |
0.54525 * 0.64842 * 0.77111 * 0.917 |
|
Q3 |
0.4585 * 0.54525 * 0.64842 * 0.77111 |
|
Q4 |
0.38555 * 0.4585 * 0.54525 * 0.64842 |
|
Q5 |
0.32421 * 0.38555 * 0.4585 * 0.54525 |
|
Q6 |
0.27263 * 0.32421 * 0.38555 * 0.4585 |
|
Q7 |
0.22925 * 0.27263 * 0.32421 * 0.38555 |
|
Q8 |
0.19278 * 0.22925 * 0.27263 * 0.32421 |
|
Q9 |
0.1621 * 0.19278 * 0.22925 * 0.27263 |
|
Q10 |
0.13631 * 0.1621 * 0.19278 * 0.22925 |
|
Q11 |
0.11463 * 0.13631 * 0.1621 * 0.19278 |
|
Q12 |
0.096388 * 0.11463 * 0.13631 * 0.1621 |
|
Q13 |
0.081052 * 0.096388 * 0.11463 * 0.13631 |
|
Q14 |
0.068157 * 0.081052 * 0.096388 * 0.11463 |
|
Q15 |
0.057313 * 0.068157 * 0.081052 * 0.096388 |
5.2.5 Dimension 5
Wir haben den
Verkleinerungsfaktor 
. Tabelle:
|
Q0 |
0.75786 * 0.87055 * 1 * 1.1487 * 1.3195 |
|
Q1 |
0.65975 * 0.75786 * 0.87055 * 1 * 1.1487 |
|
Q2 |
0.57435 * 0.65975 * 0.75786 * 0.87055 * 1 |
|
Q3 |
0.5 * 0.57435 * 0.65975 * 0.75786 *
0.87055 |
|
Q4 |
0.43528 * 0.5 * 0.57435 * 0.65975 * 0.75786 |
|
Q5 |
0.37893 * 0.43528 * 0.5 * 0.57435 *
0.65975 |
|
Q6 |
0.32988 * 0.37893 * 0.43528 * 0.5 *
0.57435 |
|
Q7 |
0.28717 * 0.32988 * 0.37893 * 0.43528 *
0.5 |
|
Q8 |
0.25 * 0.28717 * 0.32988 * 0.37893 *
0.43528 |
|
Q9 |
0.21764 * 0.25 * 0.28717 * 0.32988 *
0.37893 |
|
Q10 |
0.18946 * 0.21764 * 0.25 * 0.28717 *
0.32988 |
|
Q11 |
0.16494 * 0.18946 * 0.21764 * 0.25 *
0.28717 |
|
Q12 |
0.14359 * 0.16494 * 0.18946 * 0.21764 *
0.25 |
|
Q13 |
0.125 * 0.14359 * 0.16494 * 0.18946 *
0.21764 |
|
Q14 |
0.10882 * 0.125 * 0.14359 * 0.16494 *
0.18946 |
|
Q15 |
0.094732 * 0.10882 * 0.125 * 0.14359 *
0.16494 |
Wir haben bei Q0 die 1 als mittlere KantenlŠnge. Generell ist das so bei ungeraden Dimensionen, da bei einer geometrischen Folge mit ungerader Gliederzahl der Median gleich dem geometrischen Mittel ist.