Hans Walser, [20120608]
DIN-Raster und Quadratraster
1 Die Raster
1.1
DIN-Raster
DIN-Raster gibt es im
Hochformat und im Querformat. Es gibt verschiedene Darstellungsarten, als
Flchen-, Linien- oder Punktraster.

DIN-Raster als
Flchenraster
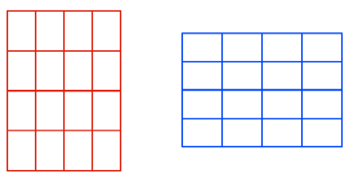
Linienraster
Ein Linienraster
erhalten wir, wenn wir ein A4-Papier mehrfach falten und dann wieder auffalten.

Faltraster

Punktraster
Ein Punktraster ergibt
sich auch, wenn wir ein A4-Papier mehrfach falten, dann alle Ecken ein bisschen
abschneiden und dann wieder auffalten.

Scherenschnitt
Die Raster im
Hochformat und im Querformat sind nicht kompatibel: Wenn wir einen Rasterpunkt
des Hochformat-Rasters auf einen Rasterpunkt des Querformat-Rasters legen, gibt
es auch bei unendlich ausgedehnten Rastern keine weiteren gemeinsamen
Rasterpunkte mehr.
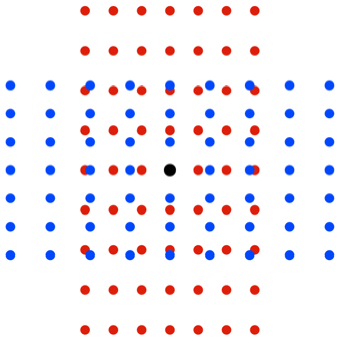
Nur ein Punkt ist in
beiden Rastern
Beweis wie blich in
solchen Sachen indirekt: Wir nehmen einen weiteren gemeinsamen Rasterpunkt an.
Beim Rechteck mit rasteparallelen Seiten und den beiden gemeinsamen
Rasterpunkten als diametrale Ecken sind dann auch die beiden anderen Ecken
gemeinsame Rasterpunkte. Die horizontale Seite dieses Rechteckes setzt sich
also einerseits aus n kurzen Rasterseiten
(der Lnge 1) und andererseits aus m
langen Rasterseiten (der Lnge ![]() ) zusammen. Somit haben wir:
) zusammen. Somit haben wir:
![]()
Dies steht im
Widerspruch zur Irrationalitt von ![]() .
.
1.2
Quadratraster
Das Quadratraster
kennen alle von der Schule her.
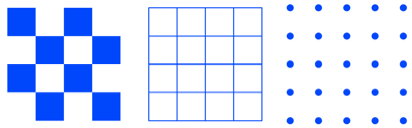
Quadratraster
2
Unterteilen
2.1
Halbieren
2.1.1
DIN-Raster
DIN-Raster knnen
flchenm§ig durch eine Schar von Mittelparallelen halbiert werden. Aus dem
Hochformat-Raster wird ein Querformat-Raster und umgekehrt. Die Rasterlinien
des alten Rasters sind auch Rasterlinien des neuen Rasters.
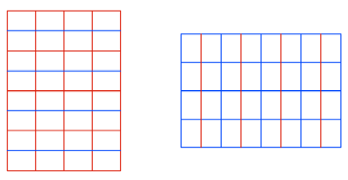
Flchenm§ige Halbierung
Frage: Was ergibt
sich, wenn wir mit Diagonalen gem§ Abbildung arbeiten? (Anregung: Peter
Gallin, Zrich)
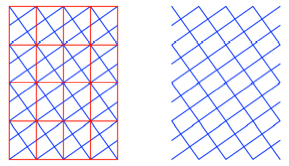
Und?
Wer meint, das Bild
rechts hnge schief im Satzspiegel, darf ber optische Tuschungen
nachdenken.
Bearbeitung
Es ergibt sich ein
flchenm§ig gedritteltes DIN-Raster.
Zum Nachweis setzen wir
die Schmalseite des Ausgangsraster 1, die Langseite ist ![]() . Der Flcheninhalt eines Rasterrechteckes ist
. Der Flcheninhalt eines Rasterrechteckes ist ![]() .
.
Eine Diagonale von
links unten nach rechts oben hat dann die Lnge
![]()
Eine Diagonale von
links oben nach rechts unten im Nachbarrechteck ist eine um 90¡ gedreht und den
Faktor ![]() verlngerte
Kopie der Diagonale von links unten nach rechts oben. Sie hat somit die Lnge
verlngerte
Kopie der Diagonale von links unten nach rechts oben. Sie hat somit die Lnge ![]() .
.
Das rote Raster ist
also orthogonal, die Schmalseiten messen, wie aus der Figur abgelesen werden
kann, ![]() und die
Langseiten
und die
Langseiten ![]() . Das rote Raster hat also die DIN-Verhltnisse. Ein
Rasterrechteck hat den Flcheninhalt
. Das rote Raster hat also die DIN-Verhltnisse. Ein
Rasterrechteck hat den Flcheninhalt ![]() , also einen Drittel des Flcheninhalts eines Rechtecks des
Ausgangsrasters.
, also einen Drittel des Flcheninhalts eines Rechtecks des
Ausgangsrasters.
Diese Flchendrittelung
kann mit einem Zerlegungsbeweis unmittelbar eingesehen werden.
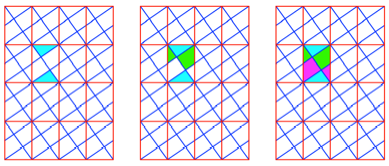
Zerlegungsbeweis
Frage: Was ergibt
sich, wenn wir mit Diagonalen gem§ Abbildung arbeiten?
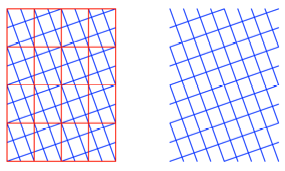
Kleines Raster?
Bearbeitung
Fr die Schmalseite der
neuen Rasterrechtecke ergibt sich ![]() . Fr die Langseite erhalten wir
. Fr die Langseite erhalten wir ![]() . Das DIN-Verhltnis ist erfllt. Der Flcheninhalt ist
. Das DIN-Verhltnis ist erfllt. Der Flcheninhalt ist ![]() . Das blaue Raster bedeutet also flchenm§ig eine Reduktion
mit dem Faktor
. Das blaue Raster bedeutet also flchenm§ig eine Reduktion
mit dem Faktor ![]() . Es gibt auch einen Zerlegungsbeweis.
. Es gibt auch einen Zerlegungsbeweis.
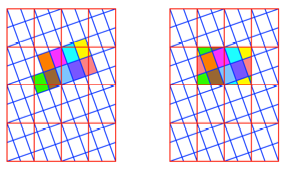
Zwei Neuntel
Frage: Was ergibt
sich, wenn wir mit Diagonalen gem§ Abbildung arbeiten?
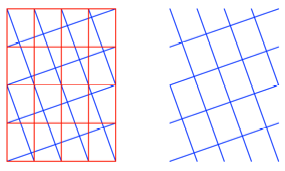
Und?
Bearbeitung
Gegenber dem
vorhergehenden Beispiel erhalten wir das Vierfache, also ![]() . Somit fast so gro§ wie ein Rechteck im Ausgangsraster.
. Somit fast so gro§ wie ein Rechteck im Ausgangsraster.
Frage: Was ergibt
sich, wenn wir mit Diagonalen gem§ Abbildung arbeiten?
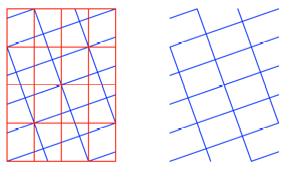
Und?
Bearbeitung
Die Rechtecke der
beiden Raster sind gleich gro§: Im blauen Raster ergibt sich fr die
Schmalseite eines Rasterrechteckes ![]() uns fr die Langseite
entsprechend
uns fr die Langseite
entsprechend ![]() .
.
Das blaue Raster ergibt
sich durch Spiegelung des Ausgangsrasters an einer Rasterdiagonalen.
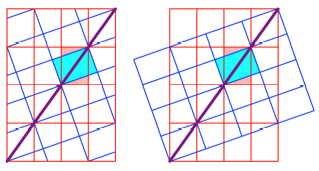
Spiegelung
Frage: Gibt es andere Spiegelungsmglichkeiten?
Bearbeitung
Die Abbildung zeigt
eine andere mgliche Spiegelachse. Sie ist rechtwinklig zur obigen
Spiegelachse.
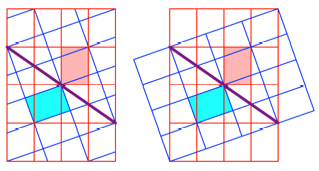
Andere Spiegelachse
Das blaue Raster ergibt
sich aber auch durch eine Drehung um einen Rasterpunkt um den eingezeichneten
Winkel.
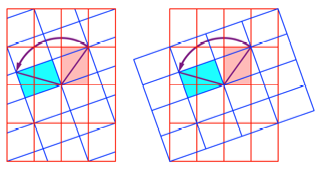
Drehung
Dieser Winkel ist ![]() . Dieser Winkel lsst sich auf verschiedene Arten darstellen:
. Dieser Winkel lsst sich auf verschiedene Arten darstellen:
![]() .
.
Das kann mit trigonometrischen
Umformungen gezeigt werden. Aber wahrscheinlich machen Sie es wie ich, indem
Sie mit dem Taschenrechner nachprfen. Dieser Winkel ist auch der stumpfe
Schnittwinkel der beiden Diagonalen im DIN-Rechteck.
Wir haben oben gesehen,
dass die DIN-Raster in Hochformat und in Querformat, die um eine Drehung um 90¡
auseinander hervorgehen, au§er dem Drehpunkt keine weiteren Punkte mehr
gemeinsam haben. Bei einer Drehung um den Winkel ![]() ergeben sich
aber unendliche viele gemeinsame Punkte.
ergeben sich
aber unendliche viele gemeinsame Punkte.
Frage: Gibt es
andere mgliche Drehwinkel?
Bearbeitung
Wir knnen auch um den
Winkel ![]() drehen.
drehen.
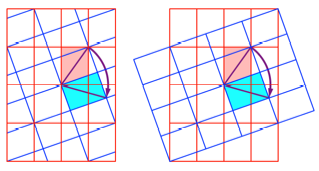
Gegendrehung
Die beiden Drehwinkel
ergnzen sich betragsm§ig auf 180¡.
Wir haben also vier Abbildungen (zwei
Spiegelungen und zwei Drehungen), welche das roten Raster auf das blaue
abbilden. Die Abbildungen sind aber unterschiedlich, wie wir aus der jeweiligen
Position des blauen Musterrechteckes sehen.
2.1.2
Quadratraster
Beim Quadratraster
arbeiten wir zum Halbieren mit den Diagonalen. Die Rasterlinien des alten
Rasters sind keine Rasterlinien des neuen Rasters.
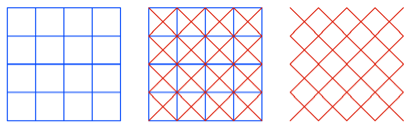
Flchenm§ige Halbierung
Frage: Was ergibt
sich, wenn wir mit schrgen Linien von Kantenmitte zu Kantenmitte arbeiten?
Bearbeitung
Wir erhalten denselben
Raster, aber versetzt.
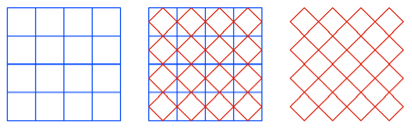
Flchenm§ige Halbierung
Frage: Was ergibt
sich, wenn wir mit schrgen Linien gem§ Abbildung arbeiten?
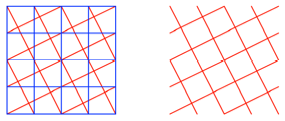
Neuer Raster?
Bearbeitung
Die neuen Quadrate sind
flchenm§ig ![]() der alten
Rasterquadrate. Zerlegungsbeweis.
der alten
Rasterquadrate. Zerlegungsbeweis.
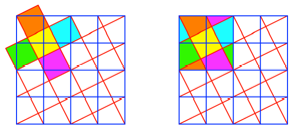
Zerlegungsbeweis
2.2
Vierteln
Das flchenm§ige
Vierteln geschieht durch lngenm§iges Halbieren. Das ist langweilig.
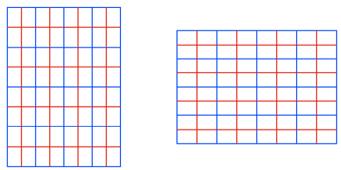
Vierteln von DIN-Rastern
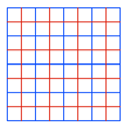
Vierteln des
Quadratrasters
3
Arbeiten im DIN-Raster
3.1
Punktraster
3.1.1
Drehung um einen rechten Winkel
Beim Drehen um einen
rechten Winkel werden Hochformat und Querformat vertauscht. Wir haben bereits
gesehen, dass wegen der Irrationalitt von ![]() au§er dem
Drehpunkt kein Rasterpunkt mit einem gedrehten Rasterpunkt bereinstimmen kann.
au§er dem
Drehpunkt kein Rasterpunkt mit einem gedrehten Rasterpunkt bereinstimmen kann.
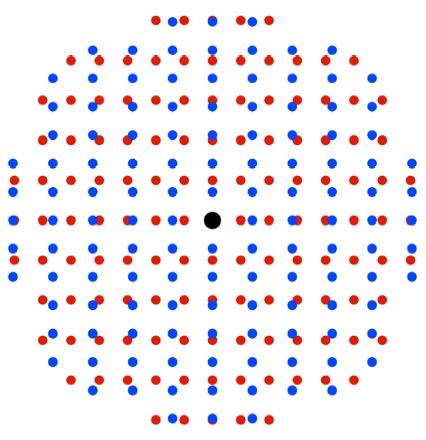
Drehen um einen rechten
Winkel
Zwar sehen wir am
rechten Bildrand in der Mitte zwei fast bereinstimmende Punkte. Wenn sie
bereinstimmen wrden, wre ![]() , also
, also ![]() . Das ist aber nur ein Nherungswert fr
. Das ist aber nur ein Nherungswert fr ![]() .
.
3.1.2
Drehen um den stumpfen Diagonalenschnittwinkel
Wenn wir um den
stumpfen Diagonalenschnittwinkel im DIN-Rechteck, also um den Winkel ![]() , drehen, haben die beiden Raster unendlich viele gemeinsame
Punkte. Es ergibt sich ein berlagerungsraster, in der Abbildung schwarz
eingezeichnet. Das berlagerungsraster hat die Spiegelachsen, welche das rote
Raster auf das blaue Raster abbilden, als Symmetrieachsen.
, drehen, haben die beiden Raster unendlich viele gemeinsame
Punkte. Es ergibt sich ein berlagerungsraster, in der Abbildung schwarz
eingezeichnet. Das berlagerungsraster hat die Spiegelachsen, welche das rote
Raster auf das blaue Raster abbilden, als Symmetrieachsen.
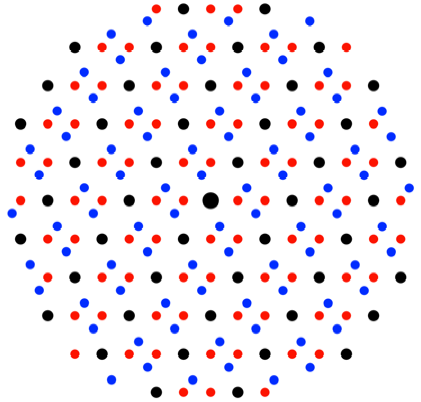
Drehen um
Diagonalenschnittwinkel
Das berlagerungsraster
bildet seinerseits Rechtecke im DIN-Verhltnis. Um das einzusehen, stellen wir
die Raster in der Gau§schen Zahlenebene der komplexen Zahlen dar.
Das ursprngliche rote
Raster besteht aus den Punkten:
![]()
Die Zahlen ![]() knnen wir als Rasterkoordinaten interpretieren. Dabei ist
knnen wir als Rasterkoordinaten interpretieren. Dabei ist ![]() die bliche x-Koordinate im kartesischen Koordinatensystem und
die bliche x-Koordinate im kartesischen Koordinatensystem und ![]() die y-Koordinate.
die y-Koordinate.
Die Drehung um den
Winkel ![]() knnen wir als
Multiplikation mit dem komplexen Faktor
knnen wir als
Multiplikation mit dem komplexen Faktor ![]() darstellen.
Dieser Faktor hat nmlich den Betrag 1 und das Argument
darstellen.
Dieser Faktor hat nmlich den Betrag 1 und das Argument ![]() . Aus den roten Rasterpunkten erhalten wir die blauen
Rasterpunkte:
. Aus den roten Rasterpunkten erhalten wir die blauen
Rasterpunkte:
![]()
Es ist also:
![]()
Wegen den Dritteln sind
nicht alle blauen Punkte auf roten Rasterpunkten.
Nun fhren wir noch
eine andere Abbildung ein, nmlich eine Drehstreckung mit dem Winkel ![]() (dies ist die
Hlfte des Drehwinkels oben) und dem Streckfaktor
(dies ist die
Hlfte des Drehwinkels oben) und dem Streckfaktor ![]() . Diese Drehstreckung knnen wir als Multiplikation mit dem
komplexen Faktor
. Diese Drehstreckung knnen wir als Multiplikation mit dem
komplexen Faktor ![]() darstellen. Dieser
Faktor hat nmlich den Betrag
darstellen. Dieser
Faktor hat nmlich den Betrag ![]() und das Argument
und das Argument
![]() . Aus den roten Rasterpunkten erhalten wir die neuen Rasterpunkte:
. Aus den roten Rasterpunkten erhalten wir die neuen Rasterpunkte:
![]()
Es ist also:
![]()
Die Punkte ![]() haben
ganzzahlige Rasterkoordinaten, sind also rote Rasterpunkte. Sie bilden ein
DIN-Raster mit der Schmalseite
haben
ganzzahlige Rasterkoordinaten, sind also rote Rasterpunkte. Sie bilden ein
DIN-Raster mit der Schmalseite ![]() und der
Langseite
und der
Langseite ![]() .
.
Nun noch eine letzte
Abbildung, nmlich die Drehstreckung mit dem Winkel ![]() und dem
Streckfaktor
und dem
Streckfaktor ![]() . Das ist die oben beschriebene Drehstreckung, aber mit dem
umgekehrten Winkel. Da der Streckfaktor nach wie vor
. Das ist die oben beschriebene Drehstreckung, aber mit dem
umgekehrten Winkel. Da der Streckfaktor nach wie vor
![]() ist, handelt es
sich aber nicht um die inverse Abbildung der oben beschriebenen Drehstreckung.
Diese neue Drehstreckung knnen wir als Multiplikation mit dem komplexen Faktor
ist, handelt es
sich aber nicht um die inverse Abbildung der oben beschriebenen Drehstreckung.
Diese neue Drehstreckung knnen wir als Multiplikation mit dem komplexen Faktor
![]() darstellen. Wir
wenden sie auf die blauen Rasterpunkte an. Aus Symmetriegrnden (Vergleich mit
der Drehstreckung oben) ergeben sich blaue Rasterpunkte. Rechnerisch erhalten
wir:
darstellen. Wir
wenden sie auf die blauen Rasterpunkte an. Aus Symmetriegrnden (Vergleich mit
der Drehstreckung oben) ergeben sich blaue Rasterpunkte. Rechnerisch erhalten
wir:
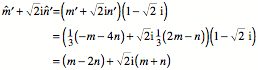
Es ist also:
![]()
Die durch ![]() beschriebenen
Punkte sind also sowohl rote wie blaue Rasterpunkte, gehren also dem in der
Abbildung schwarz eingezeichneten berlagerungsraster an. Wir wollen noch
zeigen, dass diese Punkte das ganze berlagerungsraster ausmachen. Dazu mssen
wir ausschlie§en, dass es noch berlagerungspunkte gibt, die nicht dem durch
beschriebenen
Punkte sind also sowohl rote wie blaue Rasterpunkte, gehren also dem in der
Abbildung schwarz eingezeichneten berlagerungsraster an. Wir wollen noch
zeigen, dass diese Punkte das ganze berlagerungsraster ausmachen. Dazu mssen
wir ausschlie§en, dass es noch berlagerungspunkte gibt, die nicht dem durch ![]() beschriebenen
Raster angehren. Dazu dient ein Abstandsargument. Zwei Punkte des
berlagerungsraster haben einen Minimalabstand
beschriebenen
Raster angehren. Dazu dient ein Abstandsargument. Zwei Punkte des
berlagerungsraster haben einen Minimalabstand ![]() (Diagonalenlnge
im roten Raster). Da die durch
(Diagonalenlnge
im roten Raster). Da die durch ![]() beschriebenen
Punkte DIN-Rechtecke mit der Schmalseite
beschriebenen
Punkte DIN-Rechtecke mit der Schmalseite ![]() und der
Langseite
und der
Langseite ![]() bilden, sind in
einem solchen Rechteck alle Punkte von mindestens einer Ecke weniger als
bilden, sind in
einem solchen Rechteck alle Punkte von mindestens einer Ecke weniger als ![]() entfernt.
entfernt.
Die durch ![]() beschriebenen
Punkte sind also das berlagerungsraster. Uff.
beschriebenen
Punkte sind also das berlagerungsraster. Uff.
Die Abbildung
illustriert die Drehstreckung von rot zu schwarz und die Drehung von rot zu
blau.
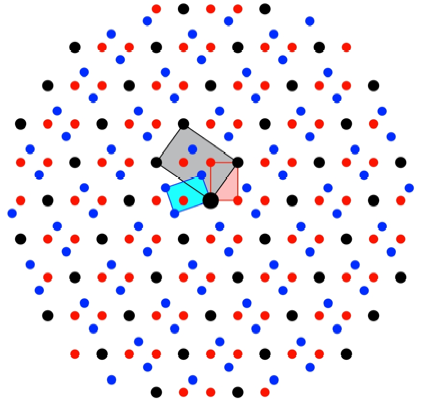
Drehstreckung und
Drehung
Es ergeben sich noch
weitere Rechtecke im DIN-Verhltnis mit abwechselnd roten und blauen Punkten.
Die kleinen haben den Flcheninhalt ![]() des Flcheninhaltes
eines Ausgangsrasterrechtecks, die mittleren sind doppelt so gro§ und die
gro§en, das sind die mit einem schwarzen Punkt in der Mitte,
des Flcheninhaltes
eines Ausgangsrasterrechtecks, die mittleren sind doppelt so gro§ und die
gro§en, das sind die mit einem schwarzen Punkt in der Mitte, ![]() des Flcheninhaltes
eines roten Ausgangsrasterrechtecks.
des Flcheninhaltes
eines roten Ausgangsrasterrechtecks.
Ferner haben wir zwei
Typen von unregelm§igen
Sechsecken mit der Eckenfarbfolge schwarz-rot-blau-schwarz-rot-blau
beziehungsweise schwarz-blau-rot-schwarz-blau-rot. Die Sechsecke der beiden
Typen haben aber denselben Flcheninhalt, nmlich ![]() des
Flcheninhaltes eines roten Ausgangsrasterrechtecks.
des
Flcheninhaltes eines roten Ausgangsrasterrechtecks.
3.1.3
Drehen um Vielfache des stumpfen Diagonalenschnittwinkels
3.1.3.1
Drehen um den doppelten stumpfen Diagonalenschnittwinkel
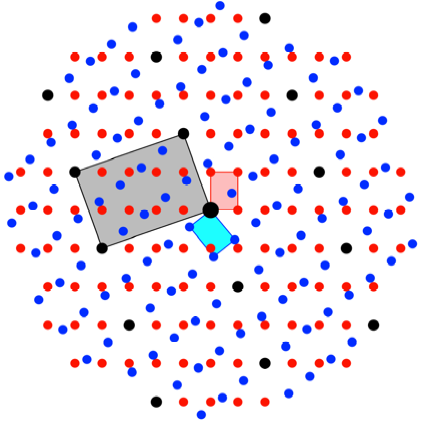
Drehen um den doppelten
Diagonalenschnittwinkel
Das berlagerungsraster
bildet wieder Rechtecke im DIN-Verhltnis. Sie haben die Schmalseite 3 und die
Langseite ![]() . Der Flcheninhalt ist das Neunfache des Flcheninhaltes
eines Ausgangsrasterrechtecks. Wir erkennen wieder eine Drehstreckung, um das
berlagerungsraster zu finden. Sie hat als Winkel das Doppelte des Winkels der
Drehstreckung oben und den Faktor 3. Sie ist somit das Quadrat der
Drehstreckung oben und kann durch den Faktor
. Der Flcheninhalt ist das Neunfache des Flcheninhaltes
eines Ausgangsrasterrechtecks. Wir erkennen wieder eine Drehstreckung, um das
berlagerungsraster zu finden. Sie hat als Winkel das Doppelte des Winkels der
Drehstreckung oben und den Faktor 3. Sie ist somit das Quadrat der
Drehstreckung oben und kann durch den Faktor ![]() beschrieben
werden.
beschrieben
werden.
3.1.3.2
Drehen um das Dreifache des stumpfen Diagonalenschnittwinkels
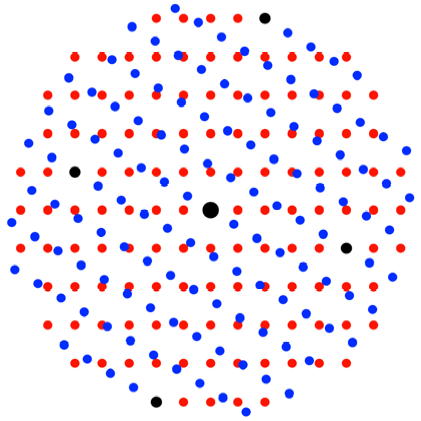
Drehen um das Dreifache
des Diagonalenschnittwinkels
Das berlagerungsraster
bildet, soweit aus der Zeichnung erkennbar, Rechtecke im DIN-Verhltnis mit der
Schmalseite ![]() , der Langseite
, der Langseite ![]() und dem Flcheninhalt
und dem Flcheninhalt
![]() .
.
3.1.3.3
Allgemein
Wir vermuten, dass wir
beim Drehen um das n-Fache des
Diagonalenschnittwinkels ein berlagerungsraster erhalten, dessen
Rechecksflchen das ![]() -Fache des Flcheninhaltes eines Ausgangsrasterrechtecks
ausmachen. Die bentigte Drehsteckung zur Konstruktion des berlagerungsrasters
kann durch
-Fache des Flcheninhaltes eines Ausgangsrasterrechtecks
ausmachen. Die bentigte Drehsteckung zur Konstruktion des berlagerungsrasters
kann durch ![]() beschrieben
werden.
beschrieben
werden.
3.2
Linienraster
3.2.1
Folgen von Rechecken
Es werden einige
Beispiele und Gegenbeispiele gezeigt, welche im DIN-Raster funktionieren.
Es ist nicht mglich,
eine Folge von aufeinander folgenden A-Rechtecken alle hochkant oder alle im
Querformat in dasselbe DIN-Raster zu packen.

Passt nicht in
DIN-Raster
Wir mssen die
Rechtecke alternierend hochkant und im Querformat legen.
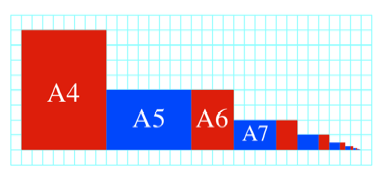
Passt in DIN-Raster
Frage: Welcher
Flchenanteil ist blau?
Bearbeitung
Fr den blauen
Flchenanteil b finden wir die
geometrische Reihe:
![]()
Das ist die schulm§ige
Lsung. Es geht aber einfacher. Die Treppe ist aus Stufenelementen der immer
gleichen Form gebaut.

Stufenelement
In jedem Stufenelement
ist ein Drittel der Flche blau. Also gilt das auch fr die gesamte Treppe.
Die Rechtecke knnen
auch anders in ein DIN-Raster gepackt werden. Wir sehen, dass die gesamte
farbige Flche dem Flcheninhalt eines A3-Rechteckes entspricht.
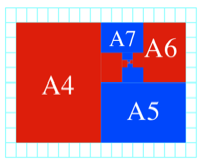
Andere Packung
Frage: Wo ist der
ãBrennpunktÒ?
Bearbeitung
Der ãBrennpunktÒ ist
der Schnittpunkt der beiden eingezeichneten Diagonalen.
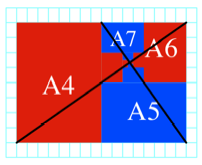
ãBrennpunktÒ
Die Rechtecke knnen zu
einem DIN-Turm zusammengesetzt werden. Der Turm passt in ein DIN-Raster.

DIN-Turm
Frage: Wie hoch ist
der Turm?
Bearbeitung
Der rot-blaue Sockel
macht hhenm§ig genau die Hlfte des gesamten Turmes aus. Mit der Basisbreite a des Turmes erhalten wir die Hhe
![]()
Die Turmhhe ist also
drei Mal die Hhe des roten Sockelteils.
3.2.2 Spiralen
Die folgenden Spiralen
sind Sonderflle von Folgen von Rechtecken, sozusagen aufgewickelte Trme.
Fragen: Welche der
folgenden Spiralen passen in ein DIN-Raster?

Spirale 1

Spirale 2

Spirale 3
Antworten
Spirale 1: ok.
Spirale 2: Die Spitzen
der rechtwinklig gleichschenkligen Dreiecke sind keine Rasterpunkte.
Spirale 3: ok.
4
Arbeiten im Quadratraster
Frage: Wir kann eine
Quadratfolge, deren Flchen fortlaufend halbiert sind, in ein Quadratraster
gepackt werden?
Bearbeitung
Es muss jedes zweite
Quadrat schrg gestellt werden.
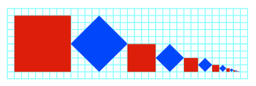
Quadratfolge
Frage: Welche der
folgenden Spiralen passen in ein Quadratraster?
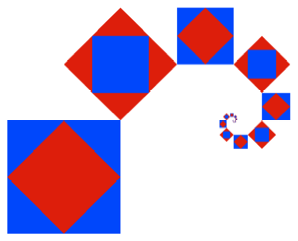
Spirale 1

Spirale 2
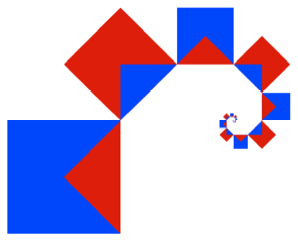
Spirale 3

Spirale 4

Spirale 5

Spirale 6
Spirale 7

Spirale 6
Antwort
Alle Spiralen passen in
ein Quadratraster.