Hans Walser, [201200902]
DIN-Spirale
Die Schlange war schlauer als alle Tiere des Feldes, die Gott gemacht
hatte.
Gen 3,1.
1 DIN-Format
Brillenschlange: Aus einem DIN A4 Papier erhalten wir durch Halbieren zwei DIN A5 Papiere. Diese haben dasselbe Seitenverhltnis wie das DIN A4 Papier, sie sind also hnlich.
Dann knnen wir weiter halbieren und erhalten die Folge A5, A6, A7, ... (Abb. 1).
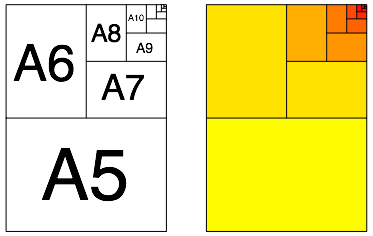
Abb. 1: Unterteilung des DIN A4 Papiers
Kobra: Da gibt es so eine Treppe (Abb. 2).
Kreuzotter: Die hat aber megaviele Stufen.
Viper: Und ist trotzdem nur so hoch wie das Papierrechteck.
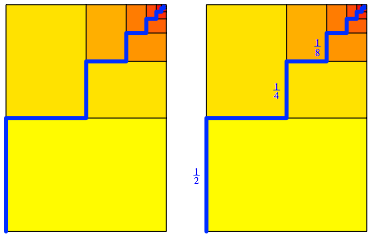
Abb. 2: Treppe und Stufen
Brillenschlange: Also die gesamte Hhe ist gleich viel wie ein Halbes plus ein Viertel plus ein Achtel plus und so weiter —
Ringelnatter: Wie geht es weiter?
Brillenschlange: Plus ein Sechzehntel plus ein Zweiunddrei§igstel plus ein Vierundsechzigstel plus —
Ringelnatter: Danke, es reicht.
Brillenschlange: In Brchen aufgeschrieben:
![]()
Ringelnatter: Gut, dass die Stufen immer weniger hoch werden, sonst htten wir eine Himmelstreppe.
Brillenschlange: Wir knnen aber die Teilrechtecke auch spiralfrmig anordnen (Abb. 3).
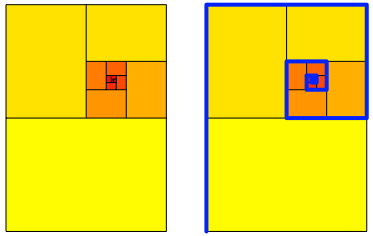
Abb. 3: Spiralfrmig Anordnung
Ringelnatter: Bisschen eckig, die Spirale. Kann ich besser (schlngelt sich in eine Spirale, Abb. 4).
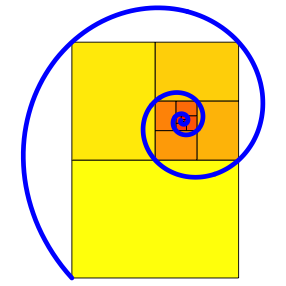
Abb. 4: Ringelnatter
Kreuzotter: Wie lang ist die eckige blaue Spirale?
Viper: Das ist einfach. Die eckige blaue Spirale ist gleich lang wie der Umfang des Rechtecks (Abb. 5).

Abb. 5: Spiralenlnge
Kreuzotter: Es gibt noch andere Mglichkeiten, eine eckige Spirale einzuzeichnen. Zum Beispiel Diagonalen oder Mitte-Mitte (Abb. 6).
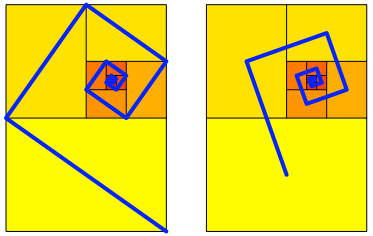
Abb. 6: Weitere Spiralen
Brillenschlange: Diese eckigen Spiralen haben doch alle die gleich Form. Sie sind nur unterschiedlich gro§.
Kobra: Und die haben auch alle dasselbe Zentrum. Das Zentrum ist im Drittelpunkt rechts oben (Abb. 7). Also Dritteln durch Halbieren.
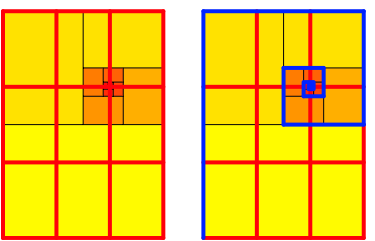
Abb. 7: Dritteln
Kreuzotter: Warum ist das so?
Viper: Welches DIN-Format hat ein kleines rotes Rechteck?
Ringelnatter: Knnen wir den Drittelpunkt auch ohne unendliches Halbieren finden?
Brillenschlange: Gibt es au§er den DIN Rechtecken andere Figuren, welche in zwei zur Ausgangsfigur hnliche Hlften zerlegt werden knnen?
Kobra: Immer mit der Ruhe. Schauen wir das mal in der senkrechten Richtung an. Die blaue Spirale geht zuerst Eins hoch, dann ein Halbes hinunter, dann einen Viertel hinauf, einen Achtel runter und so weiter und so fort (Abb. 8).
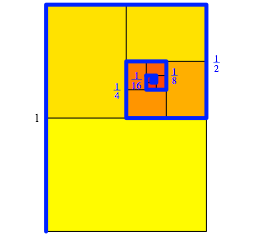
Abb. 8: Hhenanteile
Das macht:
![]()
Ringelnatter: Verstehe Bahnhof.
Kobra: Na, dann rechnen wir ein bisschen. Bei der Treppe (Abb. 2) sahen wir:
![]()
Wir vertauschen links und rechts und geben je eins dazu:
![]()
Und jetzt gruppieren wir links um:
![]()
Die zweite Klammer ist die Hlfte der ersten Klammer:
![]()
Also ist anderthalb mal die erste Klammer gleich 2 und die erste Klammer gleich vier Drittel. Die andere Klammer ist dann zwei Drittel.
Und nun zu unserem aktuellen Problem:
![]()
Wir gruppieren um:
![]()
Die beiden Klammern kennen wir aber. Wir erhalten die Differenz von vier Dritteln und zwei Dritteln, also zwei Drittel.
Ringelnatter: Danke.
Kobra: Analog knnen wir von links nach rechts berlegen. Das Zentrum ist also zwei Drittel von unten und zwei Drittel von links.
Viper: Das DIN-Format
eines kleinen roten Rechtecks in Abbildung 7 habe ich mir nun berlegt. Recht
neckisch. Ein rotes Rechteck hat ![]() der Flche
des ursprnglichen DIN A4 Papieres. Nun ist:
der Flche
des ursprnglichen DIN A4 Papieres. Nun ist:
|
Format |
Flchenanteil von A4 |
|
A4 |
1 |
|
A5 |
|
|
A6 |
|
|
A7 |
|
|
A8 |
|
Das kleine rote Rechteck ist flchenm§ig zwischen A7 und A8, nher bei A7, aber es geht nicht auf. Die Rechnung geht so: Das rote Rechteck habe das Format Ax. Dann muss folgendes gelten:
![]()
Das ist eine Exponentialgleichung mit der Lsung:
![]()
Das kleine rote Rechteck hat also etwa das Format A 7.169925.
Ringelnatter: Den Drittelpunkt finden wir einfacher mit zwei Strichen. Das geht sogar auf zwei verschiedene Arten (Abb. 9). Die beiden Strecken sind jeweils rechtwinklig zueinander.
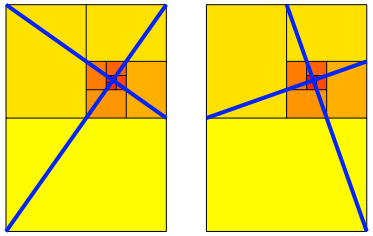
Abb. 9: Zentrum mit je zwei Strecken
Kreuzotter: Warum sind die beiden Strecken jeweils rechtwinklig?
Ringelnatter: Sag ich dir spter. Ich gehe jetzt schlafen.
Kreuzotter: Faules Stck. Typisch Ringelnatter.
Ringelnatter: Na dann
also gut: Die obere Hlfte ist eine verkleinerte und um 90¡ gedrehte Kopie des
Ganzen (Abb. 10). Verkleinert wird auf ![]() . Das ist genau der Prozentsatz, wenn du beim Kopierer
von A4 auf A5 verkleinerst. Voil.
Jetzt gehe ich aber wirklich schlafen.
. Das ist genau der Prozentsatz, wenn du beim Kopierer
von A4 auf A5 verkleinerst. Voil.
Jetzt gehe ich aber wirklich schlafen.
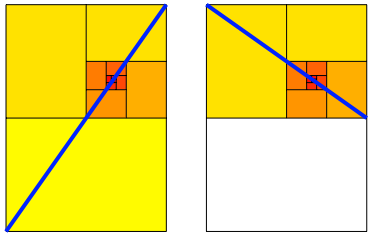
Abb. 10: Die untere Hlfte ist eine Kopie des Ganzen.
Brillenschlange: Warte noch, ich habe da eine Idee. Die Frage war doch, ob es auch andere Figuren gibt, bei denen man nach dem Halbieren zwei zur Ausgangsfigur hnliche Figuren erhlt. Dazu nehmen wir ein Origami-Papier —
Kobra: Was ist ein Origami-Papier?
Brillenschlange: Ein quadratisches Papier. Der Name kommt aus Japan. Dieses Quadrat halbieren wir lngs einer Diagonalen —
Kobra: Aber hallo, dann sind die beiden Hlften ja Dreiecke und nicht hnlich zum Ausgangsquadrat (Abb. 11)!

Abb. 11: Quadrat halbieren
Brillenschlange: Es geht auch nicht um das Quadrat, sondern um ein solches Dreieck, ein rechtwinklig-gleichschenkliges Dreieck, wie man in der Schule sagt. Halbieren wir ein solches Dreieck lngs der Symmetrieachse, erhalten wir zwei flchenm§ig halb so gro§e rechtwinklig-gleichschenklige Dreiecke. Und wir knnen weiter halbieren (Abb. 12). Es gibt eine Zickzack-Linie mit jeweils gr§eren Zicks als Zacks.
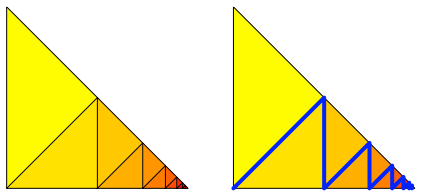
Abb. 12: Zickzack
Kobra: Kannst du es auch mit einer Spirale?
Brillenschlange: Und ob (Abb. 13).
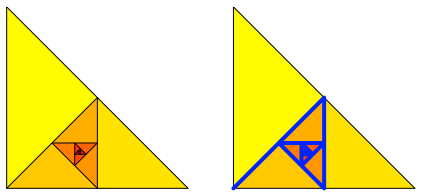
Abb. 13: Spirale
Kobra: Und wo ist hier das Zentrum?
Brillenschlange: Kannst du eigentlich selber beantworten.
Kobra: Please!
Brillenschlange: Fnfteln. Oder mit zwei Strichen (Abb. 14).
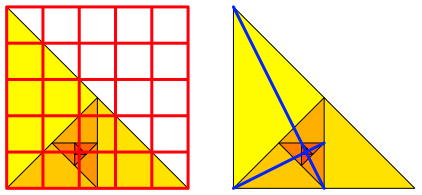
Abb. 104: Zentrum
Kobra: Das mit den Fnfteln musst du mir vorrechnen.
Brillenschlange: Gut. Aber nur, um dir meinen neuen Formel-Editor vorzufhren. In senkrechter Richtung gilt, von unten her gerechnet: ein Viertel, minus ein Sechzehntel, plus ein Vierundsechzigstel minus plus und so weiter.
![]()
In waagerechter Richtung kannst du das nun selber.
Kobra: Aber doch erstaunlich, dass es nun Fnftel gibt. Oben gab es Drittel.
Ringelnatter: Ich habe eine andere Spirale gebaut (Abb. 15).
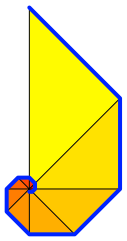
Abb. 15: Andere Spirale
Kreuzotter: Ich auch (Abb. 16).
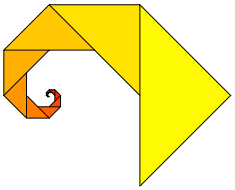
Abb. 16: Noch eine Spirale
Brillenschlange: Du kannst vier solche Spiralen zu einem Quadrat zusammensetzen (Abb. 17).

Abb. 17: Vier Spiralen
Literatur
[Heitzer 1998] Heitzer, Johanna: Spiralen, ein Kapitel phnomenaler Mathematik. Leipzig: Klett 1998. ISBN 3-12-720044-7