Hans Walser, [20130725], [20130728]
DIN, Dreieck und Sechseck
Anregung: H. K. S., L.
1 Im DIN-Raster
In einen DIN-Raster zeichnen wir ein regelm§iges Dreieck und ein regelm§iges Sechseck gem§ Abbildung 1.
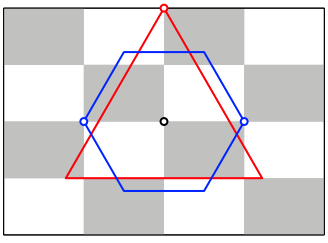
Abb. 1: Im DIN-Raster
Das Dreieck und das Sechseck sind flchengleich.
2 Rechnerischer Beweis
Ein
regelm§iges Dreieck mit dem Umkreisradius 2 und ein regelm§iges Sechseck mit
dem Umkreisradius ![]() haben beide den
Flcheninhalt
haben beide den
Flcheninhalt ![]() .
.
3 Zerlegungsgleichheit
Die Abbildungen 2 und 3 zeigen eine Zerlegungsgleichheit in zwei Schritten.
Erster Schritt: Umformung der u§eren Dreiecke und Trapeze in Parallelogramme.
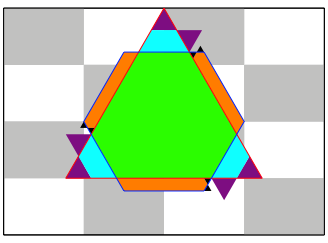
Abb. 2: Parallelogramme
Zweiter Schritt: Gemeinsame Zerlegungen der Parallelogramme.

Abb.3: Zerlegung
4 Faltgeometrie
Ausgehend von je einem DIN A4-Papier knnen wir das rote Dreieck und das blaue Sechseck auch mit Faltgeometrie herstellen. Zunchst falten wir den Raster (Abb. 4). Die Przision wir gr§er, wenn wir nicht zu viele Papierlagen bereinander falten.

Abb. 4: Falten des Rasters
Fr das Dreieck falten wir nun von links her ein gem§ Abbildung 5.
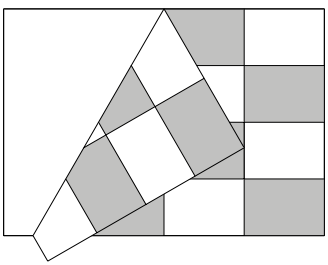
Abb. 5: Erster Faltschritt fr das Dreieck
Dieser Schritt ist entscheidend. Es entsteht oben in der Blattmitte ein Winkel von 60¡. Wir knnen und von rechts her auch einfalten und schlie§lich von unten her auf die unterste Faltlinie einfalten. Vorstehende Teile verstauen wir. Die Abbildung 6 zeigt das Faltdreieck.

Abb. 6: Faltdreieck
Fr das Sechseck falten wir zunchst auf das Viertel rechts unten und fgen eine zustzliche Faltlinie ein (Abb. 7).
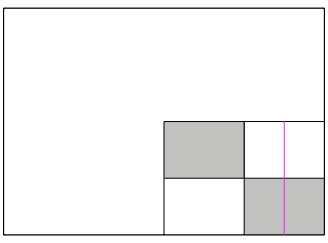
Abb. 7: Vorbereitung fr das Sechseck
Nun geht es im Prinzip weiter wie in der Abbildung 5 mit dem Dreieck (Abb. 8). Pedanten mgen nachprfen, ob die grau-wei§-Frbung des DIN-Rasters korrekt wiedergegeben ist. Eine schne bung im rumlichen Vorstellungsvermgen.
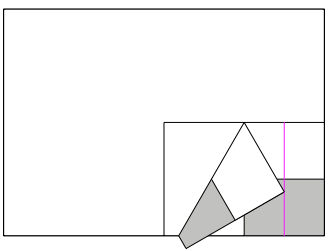
Abb. 8: Zwischenschritt fr das Sechseck
Vollstndiges Auffalten liefert die Figur der Abbildung 9.
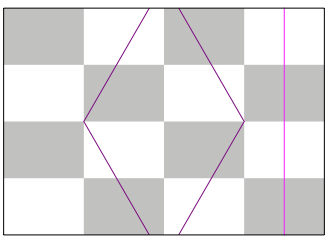
Abb. 9: Auffalten
Es fehlen noch der obere und der untere Abschluss des Sechseckes. Dazu falten wir zunchst die Mittelparallelen der schrgen Faltlinien (Abb. 10). Der Rest ist dann klar.
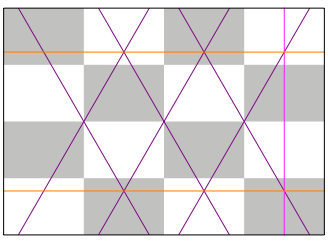
Abb. 10: Kontur des Sechsecks
Die Abbildung 11 zeigt das Faltsechseck.

Abb. 11: Faltsechseck
Das Dreieck und das Sechseck (Abb. 12) sind flchengleich.

Abb. 12: Flchengleiche Figuren