Hans Walser, [20120817a]

DIN-Format und Goldner Schnitt

1 Worum es geht

Wir konstruieren in einem DIN-Raster oder einem DIN-Rechteck mit dem Seitenverhältnis den Goldenen Schnitt.

2 Im Raster

2.1 Die Figur

In einem DIN-Raster im Querformat zeichnen wir zwei konzentrische Kreise durch die in der Abbildung 1a) angegebenen Rasterpunkte.

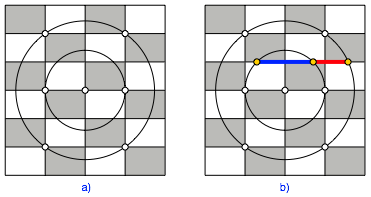
Abb. 1: Im DIN-Raster

Auf einer waagerechten Rasterlinie finden wir den Goldenen Schnitt. Der Major ist blau, der Minor rot angegeben.

2.2 Beweis

Wir arbeiten mit der Beweisfigur der Abbildung 2. Die vertikale Maschenweite wählen wir 1. Die horizontale Maschenweite ist dann .

Der kleine Kreis hat den Radius . Für den großen Kreis finden wir aus dem rechtwinkligen Dreieck RMQ den Radius .

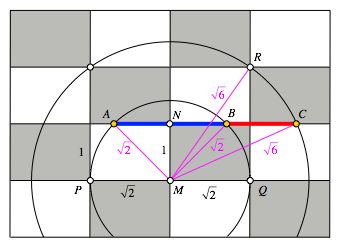
Abb. 2: Beweisfigur

Weiter erhalten wir aus dem rechtwinkligen Dreieck AMN die Länge und aus dem rechtwinkligen Dreieck MCN die Länge . Somit gilt:

3 Im DIN-Rechteck

Zu einem DIN-Rechteck zeichnen wir den Umkreis und den dazu konzentrischen Innenkreis (das ist kein Inkreis). Weiter unterteilen wir das Rechteck in acht kongruente kleinere DIN-Rechtecke. Dann ergibt sich der Goldene Schnitt gemäß Abbildung 3.

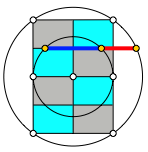
Abb. 3: Im DIN-Rechteck

Der Beweis folgt aus den Überlegungen im DIN-Raster.