Hans Walser, [20200414]
DŠcher
1 Worum geht es?
Kšrper aus zwei kongruenten regelmŠ§igen Vielecken. Interessante Dachformen.
2 Origami
Wir beginnen mit zwei Origami-Quadraten gleicher Grš§e und falten diese gemŠ§ Abbildung 1. Bergfaltlinien blau, Talfaltlinien rot.
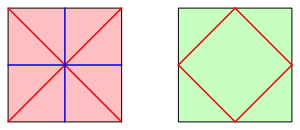
Abb. 1: Origami
Die Abbildung 2 zeigt das Realmodell. Die Form des Daches hat mich als Kind schon immer fasziniert.

Abb. 2: Origami-Papier
Die Abbildung 3 zeigt dasselbe virtuell.

Abb. 3: Dach und Bodenstźck
Nun schieben wir das Dach so auf das Bodenstźck, dass die Ecken des Dach-Origami-teils auf die Seitenmitten des Bodenstźck-Origamiteils zu liegen kommen und umgekehrt (Abb. 4).
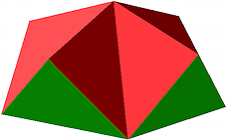
Abb. 4: Das Haus
Die Abbildung 5 zeigt das Realmodell aus Papier.

Abb. 5: Papiermodell
Bei einer KantenlŠnge s des Origamipapiers hat das Haus ein Volumen V:
![]() (1)
(1)
Die Abbildung 6 zeigt die Situation von oben. Der Umriss ist allerdings kein regelmŠ§iges Achteck.
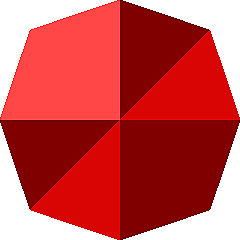
Abb. 6: Sicht von oben
3 Verallgemeinerung
Wir kšnnen das quadratische Origami-Papier ersetzen durch regelmŠ§ige n-Ecke. Im Folgenden einige Beispiele.
Die Abbildung 7 zeigt die Faltlinien fźr n = 3. Wir sehen in der DachflŠche einen Wechsel zwischen Bergfaltlinie und Talfaltlinie. Das ist fźr alle ungeraden n so.
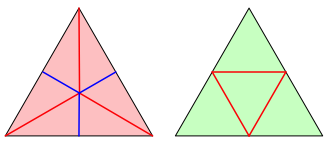
Abb. 7: Faltlinien fźr Dreiecke
Die Abbildung 8 zeigt das zugehšrige Haus.
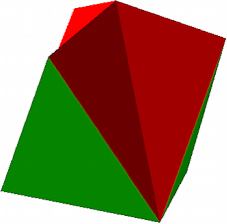
Abb. 8: n = 3
Die Abbildung 9 zeigt das Haus fźr n = 5.
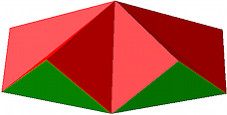
Abb. 9: n = 5
Die Abbildung 10 zeigt das Haus fźr n = 6.
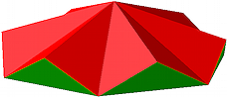
Abb. 10: n = 6
4 Koordinaten
Bezeichnungen gemŠ§ Abbildung 11.
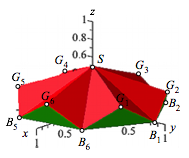
Abb. 11: Bezeichnungen
Es ist zunŠchst:
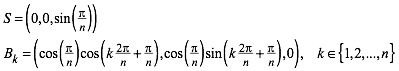 (2)
(2)
Weiter arbeiten wir mit den Hilfsgrš§en:
 (3)
(3)
Damit wird:
![]() (4)
(4)