Hans Walser, [20151206]

Davidstern

1 Worum geht es?

Verallgemeinerung des Davidsterns. Ein Schnittpunkt im Dreieck. Eine begrifflich symmetrische Figur (Selbstdualität). Alternierende Quadratsumme.

2 Eine Schnittpunkteigenschaft im Dreieck

In einem beliebigen Startdreieck (grün in Abb. 1) wählen wir einen beliebigen Punkt P und fällen die Lote auf die Dreiecksseiten (Abb. 1a). Auf jedem Lot wählen wir einen beliebigen Punkt (Abb. 1b).

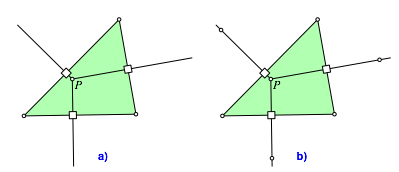
Abb. 1: Lote. Punkte auf den Loten

Nun verbinden wir diese drei Punkte zu einem Dreieck (orange in Abb. 2). Anschließend fällen wir von den Ecken des grünen Startdreieckes aus je das Lot auf eine Seite des orangen Dreiecks gemäß Abbildung 2b. Diese drei Lote schneiden sich in einem gemeinsamen Punkt Q.

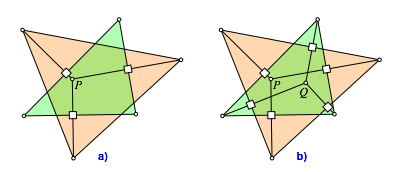
Abb. 2: Schnittpunkt Q

Die entstehende Figur (Davidstern) ist begrifflich symmetrisch oder selbstdual.

3 Alternierende Quadratsumme

Zu den Ecken des Davidsterns können wir Quadrate einzeichnen (Abb. 3), deren alternierende Flächensumme verschwindet.

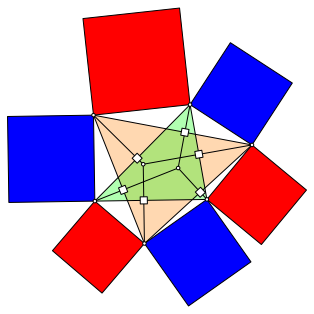
Abb. 3: Alternierende Quadrate

Für die Beweise der Schnittpunkteigenschaft und der verschwindenden alternierenden Quadratsumme siehe:

Alternierende Quadratsummen.htm

Alternierende Quadratsummen.pdf