Hans Walser, [20201017]
Davidsterne
1 Worum geht es?
Kombinatorische Spielerei am Davidstern. Anordnung basierend auf dem Dualsystem
2 Die 64 Davidsterne

Abb. 1: Die 64 Davidsterne
Keine zwei sind gleich, und es gibt keine weiteren.
Die beiden Dreiecke eines Davidsterns haben insgesamt 6 Schnittpunkte. Bei jedem Schnittpunkt kann ăobenŇ und ăuntenŇ vertauscht werden. Wir haben also bei jedem der 6 Schnittpunkte 2 Mšglichkeiten. Somit gibt es insgesamt 26 = 64 Mšglichkeiten.
Wir nummerieren die Davidsterne spaltenweise von 0 bis 63.
3 Anordnung gemŠ§ Dualsystem
Die Anordnung geschieht spaltenweise wie folgt. Jedem der sechs Schnittpunkte des Davidsterns wird eine Position im Dualsystem zugeordnet. Beginn rechts in der Mitte, dann positiver Drehsinn. Das Schnittpunktverhalten des ersten Sterns (links oben) wird an jeder Position mit 0 bewertet (Abb. 2.0).
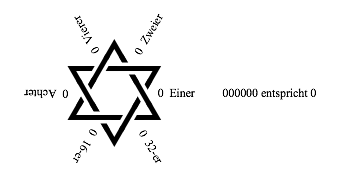
Abb. 2.0: Start
Nun setzen wir jedes Mal eine 1, wenn wir an einem Schnittpunkt ăobenŇ und ăuntenŇ vertauschen. Die folgenden Abbildungen zeigen, wie das gemeint ist.
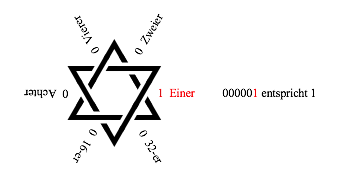
Abb. 2.1: Erster Schnittpunkt umgestellt
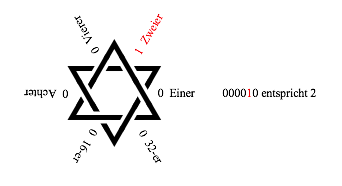
Abb. 2.2: 000010
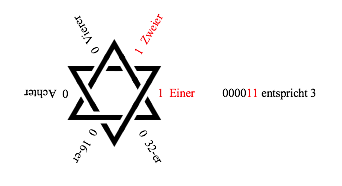
Abb. 2.3: 000011
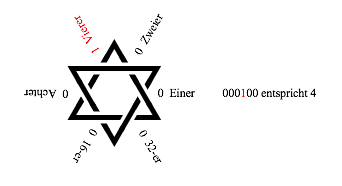
Abb. 2.4: 000100
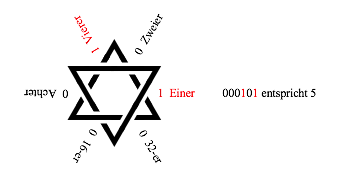
Abb. 2.5: 000101
Damit haben wir die ersten sechs Davidsterne der ersten Spalte in der Abbildung 1. Das geht jetzt so weiter bis zum letzten Davidstern rechts unten (Abb. 2.63). Hier sind alle Schalter umgestellt. Dieser Davidstern mit der Nummer 63 ist spiegelbildlich zum Davidstern mit der Nummer 0 links oben.
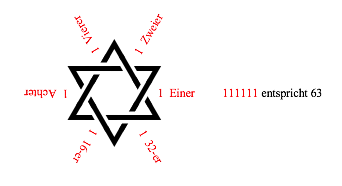
Abb. 2.63: 111111
4 Verflechtungen
Im Beispiel rechts unten in der Abbildung 1 kšnnen wir die beiden Dreiecke auseinanderziehen werden ohne sie zu zerstšren (Abb. 3.0). Solche Beispiele werden im Folgenden mit einem roten Kreis markiert.

Abb. 3.0: Keine Verflechtung
Es gibt Beispiele (Abb. 3.1) in denen die beiden Dreiecke einfach verflochten sind. Sie hŠngen ineinander wie zwei Kettenglieder.

Abb.3.1: Einfache Verflechtung
Weitere Beispiele haben ein doppelte Verflechtung (Abb.3.2).

Abb. 3.2: Zweifache Verflechtung
Schlie§lich sind die beiden Beispiele links oben und rechts unten in der Abbildung 1 sogar dreifach verflochten (Abb. 3.3). Dies sind die beiden einzigen Beispiele, die man gefźhlsmŠ§ig als ărichtigŇ bezeichnet.

Abb.3.3: Dreifache Verflechtung
Die Abbildung 4 gibt eine †bersicht.

Abb. 4: †bersicht
Die Anordnung der Farben ist punktsymmetrisch bezźglich des Mittelpunktes der quadratischen Anordnung.
Die Anordnung der Farben ist auch achsensymmetrisch bezźglich der Diagonalen von links oben nach rechts unten. Und sie ist ebenfalls achsensymmetrisch bezźglich der Diagonalen von links unten nach rechts oben.
Die Tabelle 1 gibt die Anzahlen der Farben.
|
|
Verflechtung |
Markierung |
Anzahl |
|
0 |
keine |
rot |
20 |
|
1 |
einfach |
grźn |
30 |
|
2 |
zweifach |
hellblau |
12 |
|
3 |
dreifach |
gelb |
2 |
|
|
|
|
64 |
Tab. 1: †bersicht
Weblinks
Hans Walser: Dualsystem
http://www.walser-h-m.ch/hans/Miniaturen/D/Dualsystem2/Dualsystem2.htm
Hans Walser: Dualsystem
http://www.walser-h-m.ch/hans/Miniaturen/D/Dualsystem/Dualsystem.htm
Hans Walser: OberflŠchengleiche platonische Kšrper und Kugel
www.walser-h-m.ch/hans/Miniaturen/O/Oberflaechengleich/Oberflaechengleich.htm
Hans Walser: OberflŠchengleiche platonische Kšrper und Kugel 2
www.walser-h-m.ch/hans/Miniaturen/O/Oberflaechengleich2/Oberflaechengleich2.htm