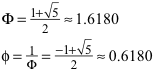Hans Walser, [20220819]

Diagonalen platonischer Körper

1     Worum geht es?

Systematische Übersicht. Diagonalen der Länge nach geordnet.

2     Die platonischen Körper

2.1     Tetraeder

Beim Tetraeder sind verschiedene Eckpunkte ausschließlich mit Kanten verbunden.

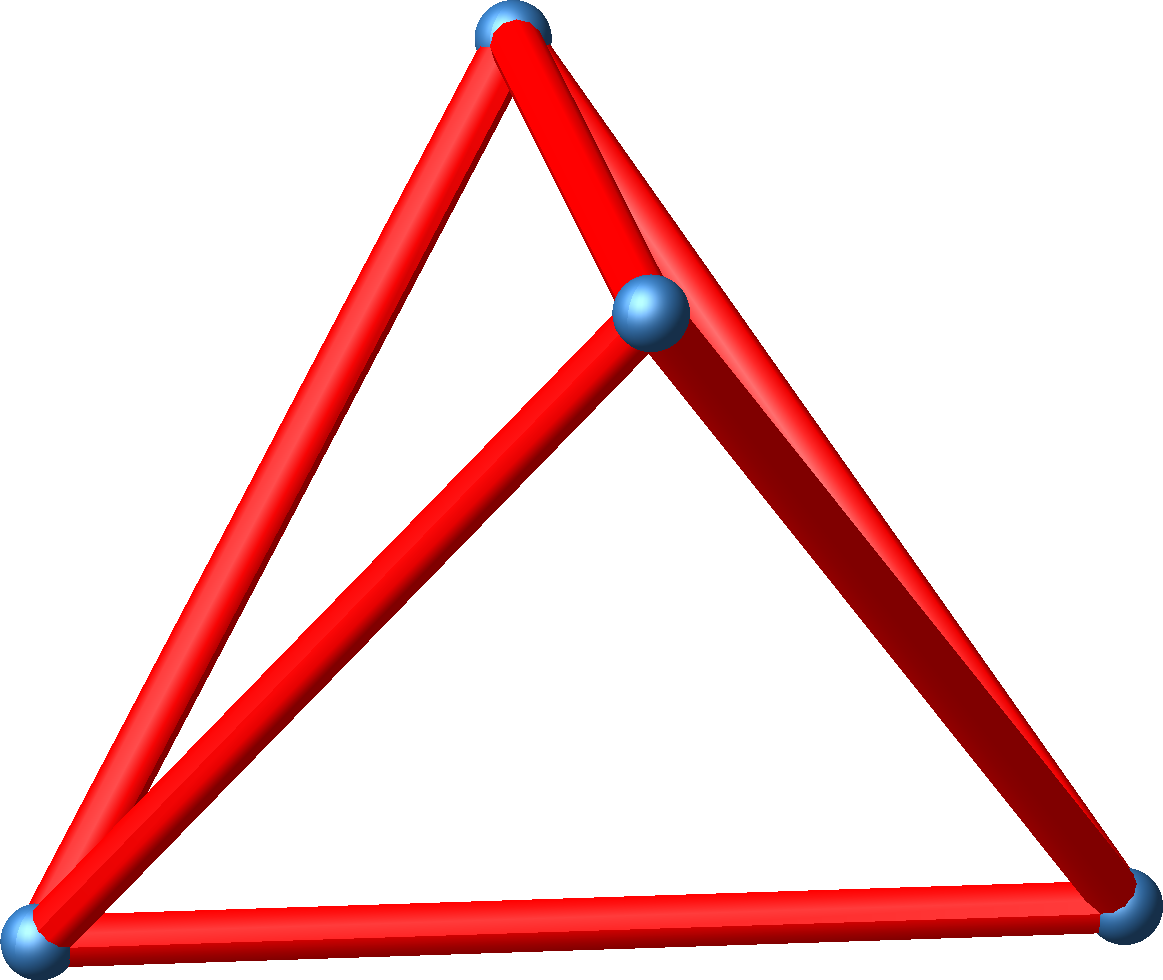
Ein Bild, das Triangel, Stativ enthält. Automatisch generierte Beschreibung

Abb. 1: Tetraeder

2.2     Oktaeder

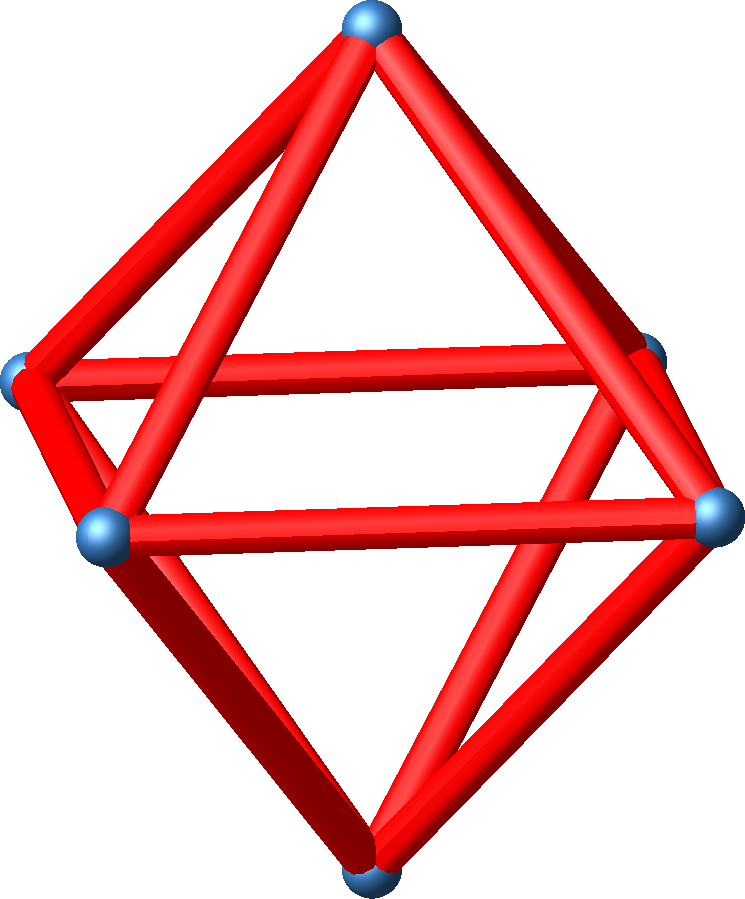
Abb. 2.1: Oktaeder

Abb. 2.2: Mittelpunktsdiagonalen

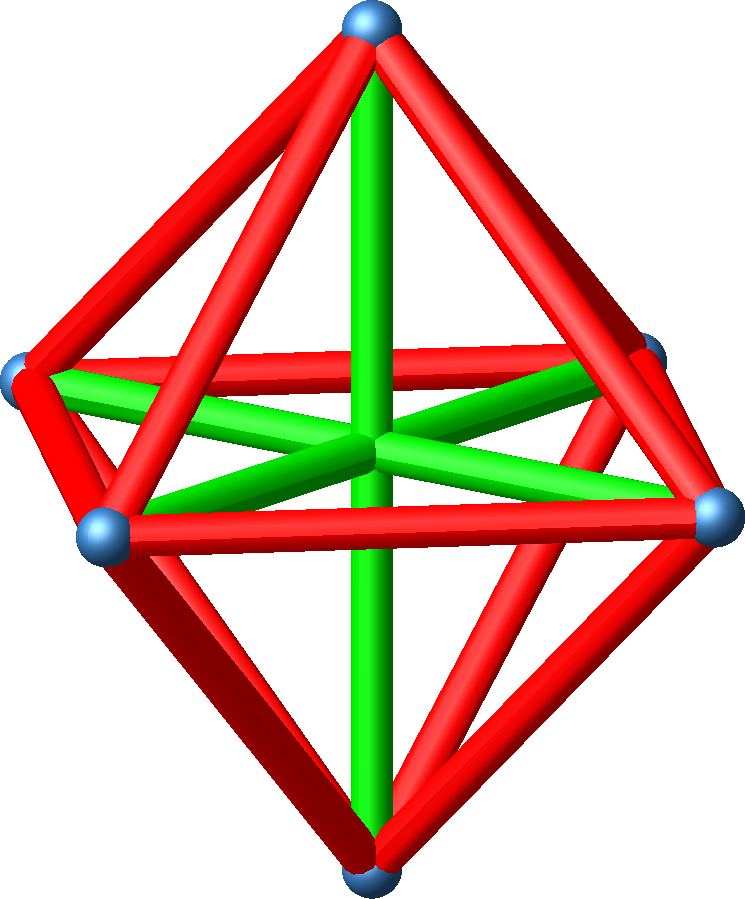
Abb. 2.3: Vollständige Darstellung

Längenverhältnis = 1 : √2.

2.3     Ikosaeder

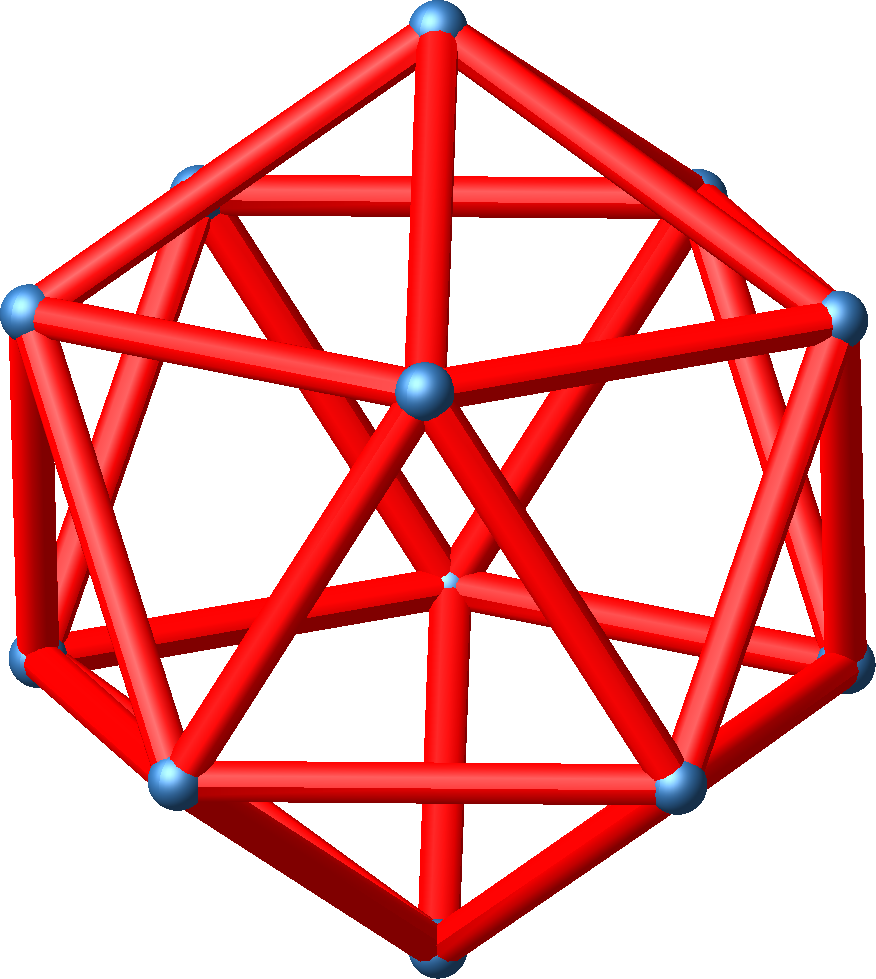
Ein Bild, das Gebäude enthält. Automatisch generierte Beschreibung

Abb. 3.1: Ikosaeder

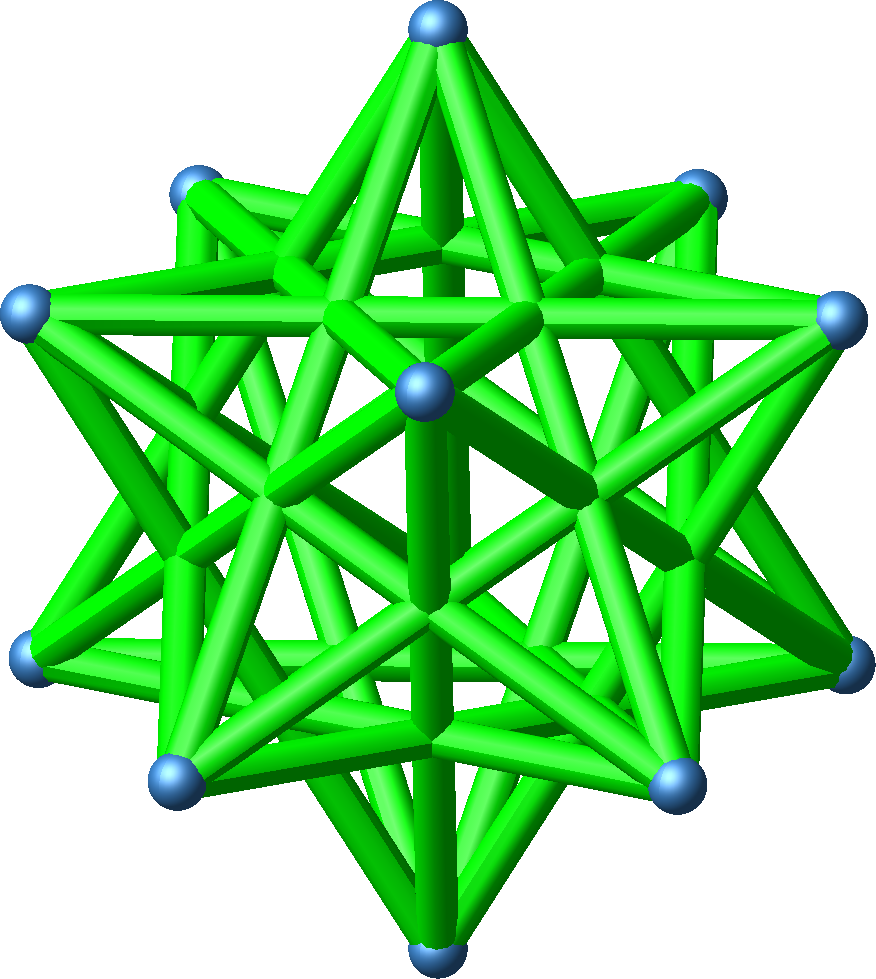
Ein Bild, das Container enthält. Automatisch generierte Beschreibung

Abb. 3.1: Dodekaederstern

Der Dodekaederstern (Abb. 3.1) ist ein Kepler-Poinsot-Körper. Er besteht aus einem Dodekaeder mit zwölf aufgesetzten Goldenen Pyramiden.

Abb. 3.3: Mittelpunktsdiagonalen

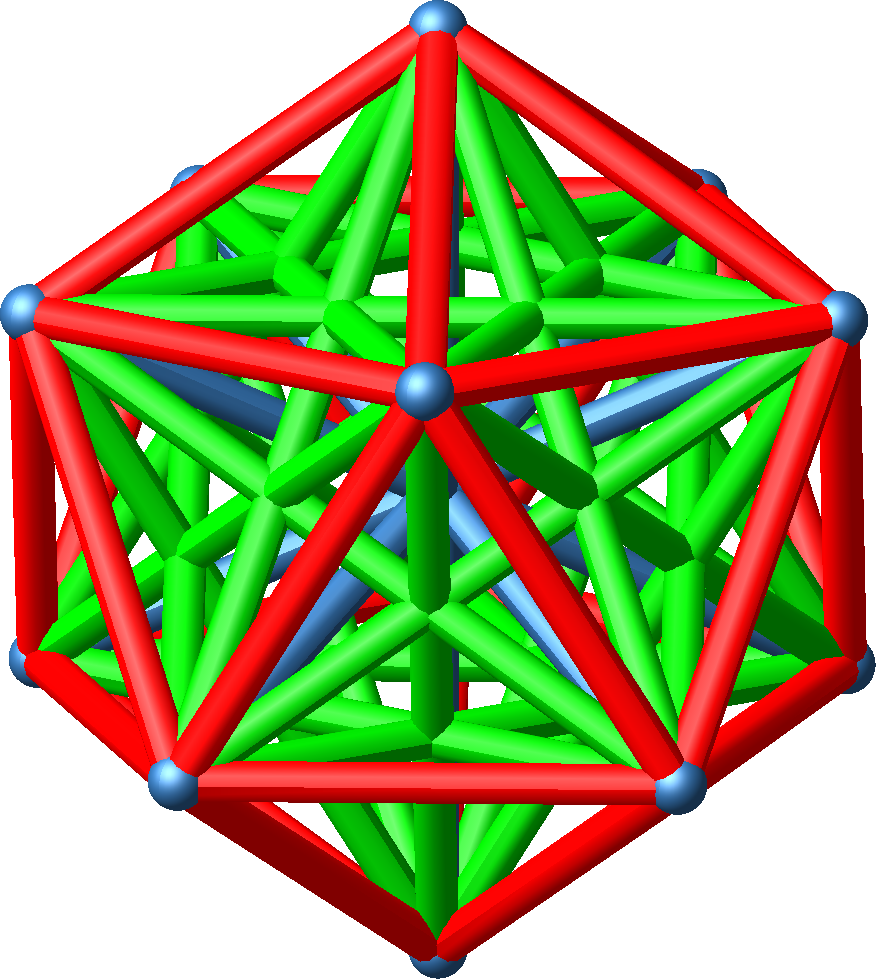
Ein Bild, das farbig, Bleistift enthält. Automatisch generierte Beschreibung

Abb. 3.4: Vollständige Darstellung

Längenverhältnis:

 

 

Dabei ist Φ der Goldene Schnitt:

 

 

2.4     Würfel (Hexaeder)

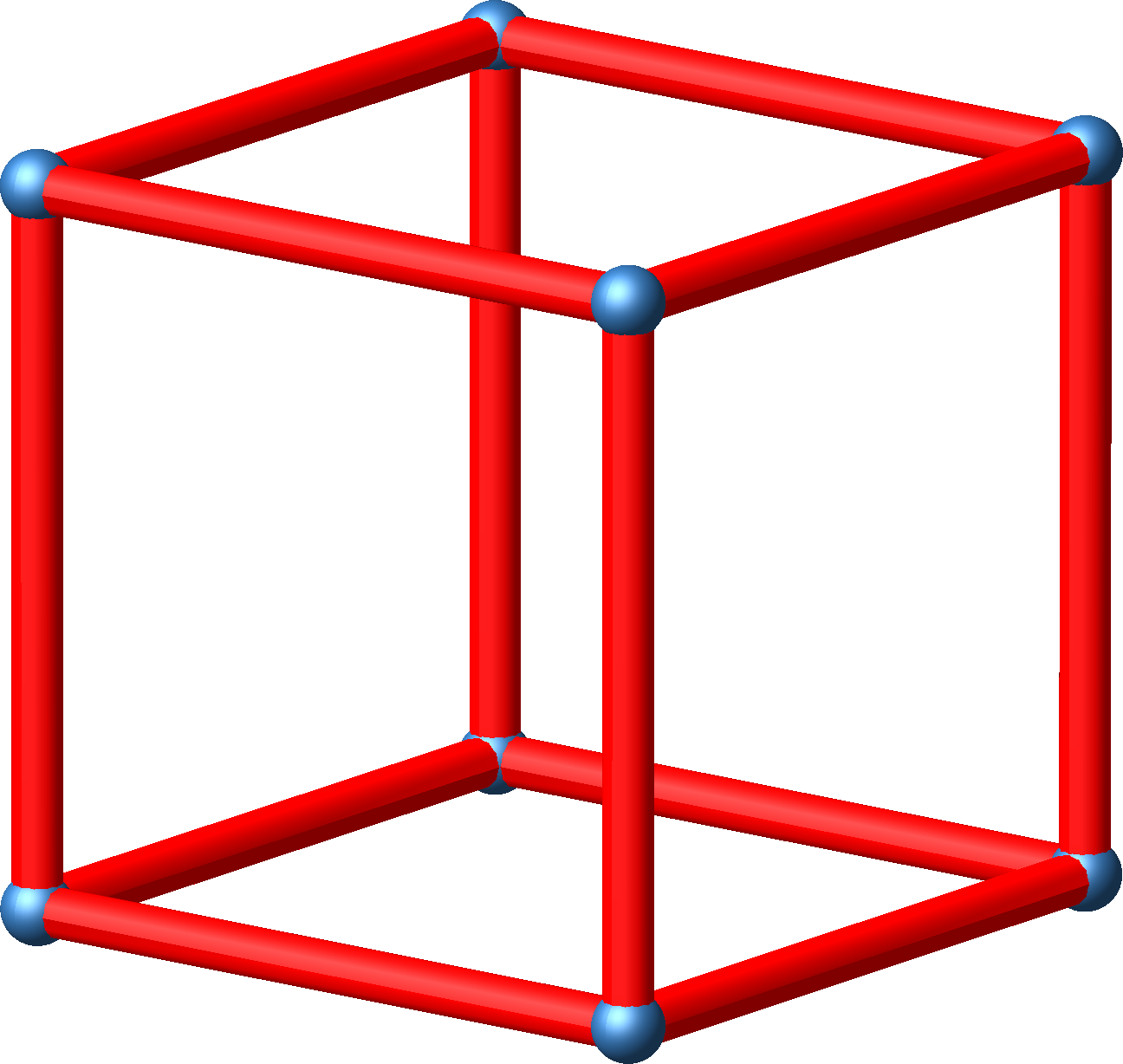
Ein Bild, das Text, Handkarren, Arbeitstisch enthält. Automatisch generierte Beschreibung

Abb. 4.1: Würfel

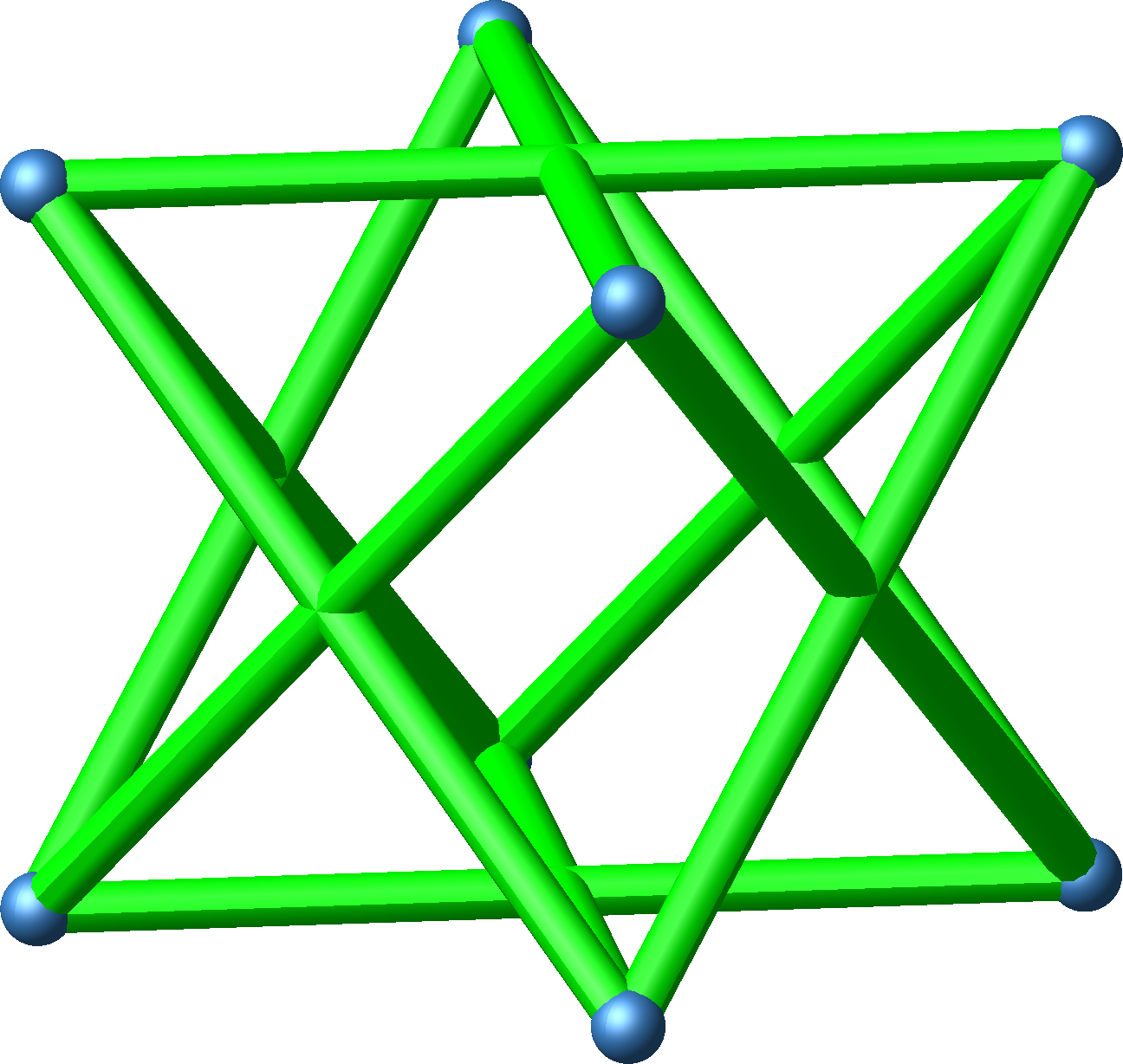
Ein Bild, das Briefpapier, Handkarren, Büroklammer enthält. Automatisch generierte Beschreibung

Abb. 4.2: Kepler-Stern

Der Kepler-Stern (stella octangula, Abb. 4.2) besteht aus einem Oktaeder mit acht aufgesetzten Tetraedern.

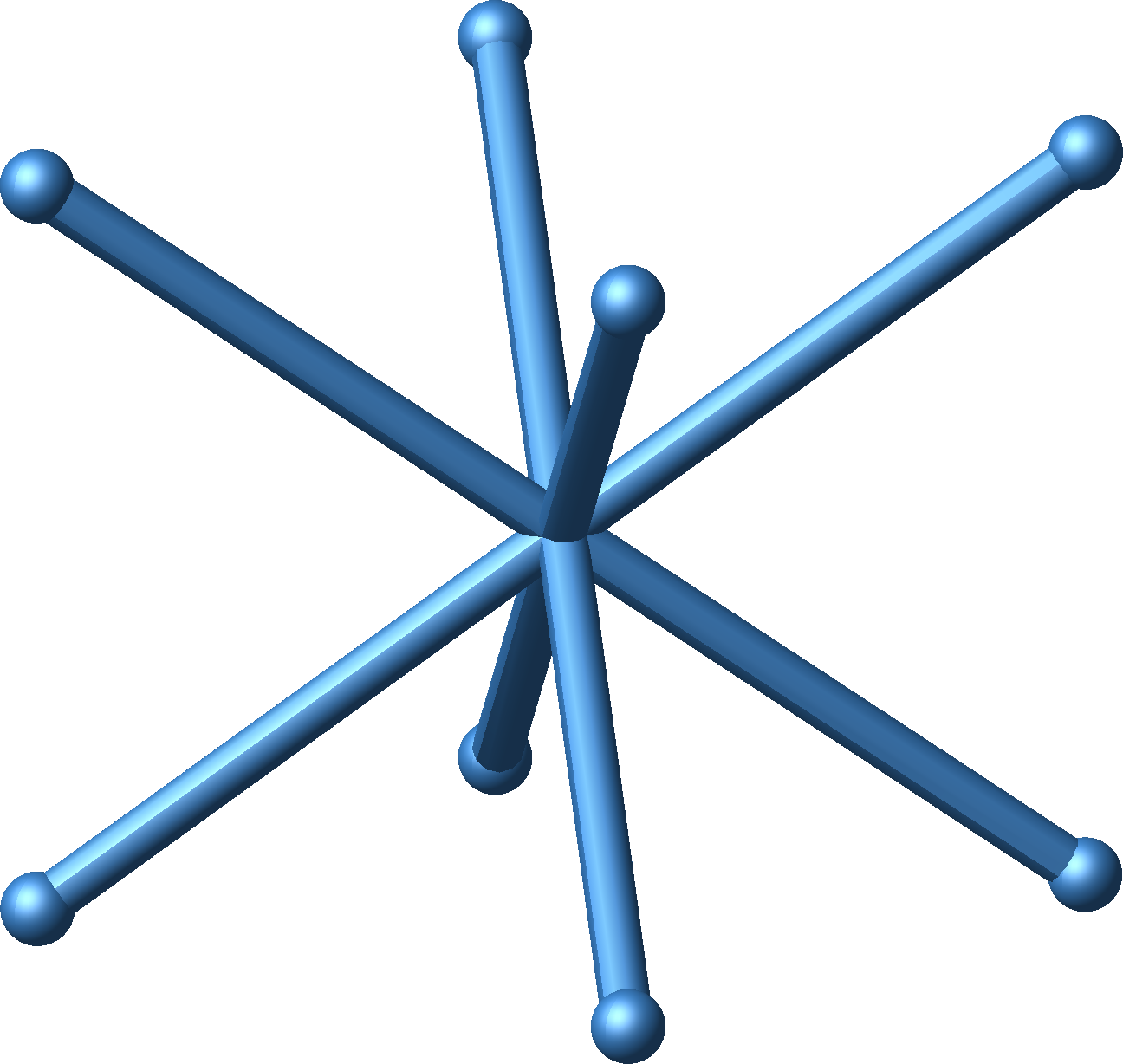
Ein Bild, das Baseball enthält. Automatisch generierte Beschreibung

Abb. 4.3: Mittelpunktsdiagonalen

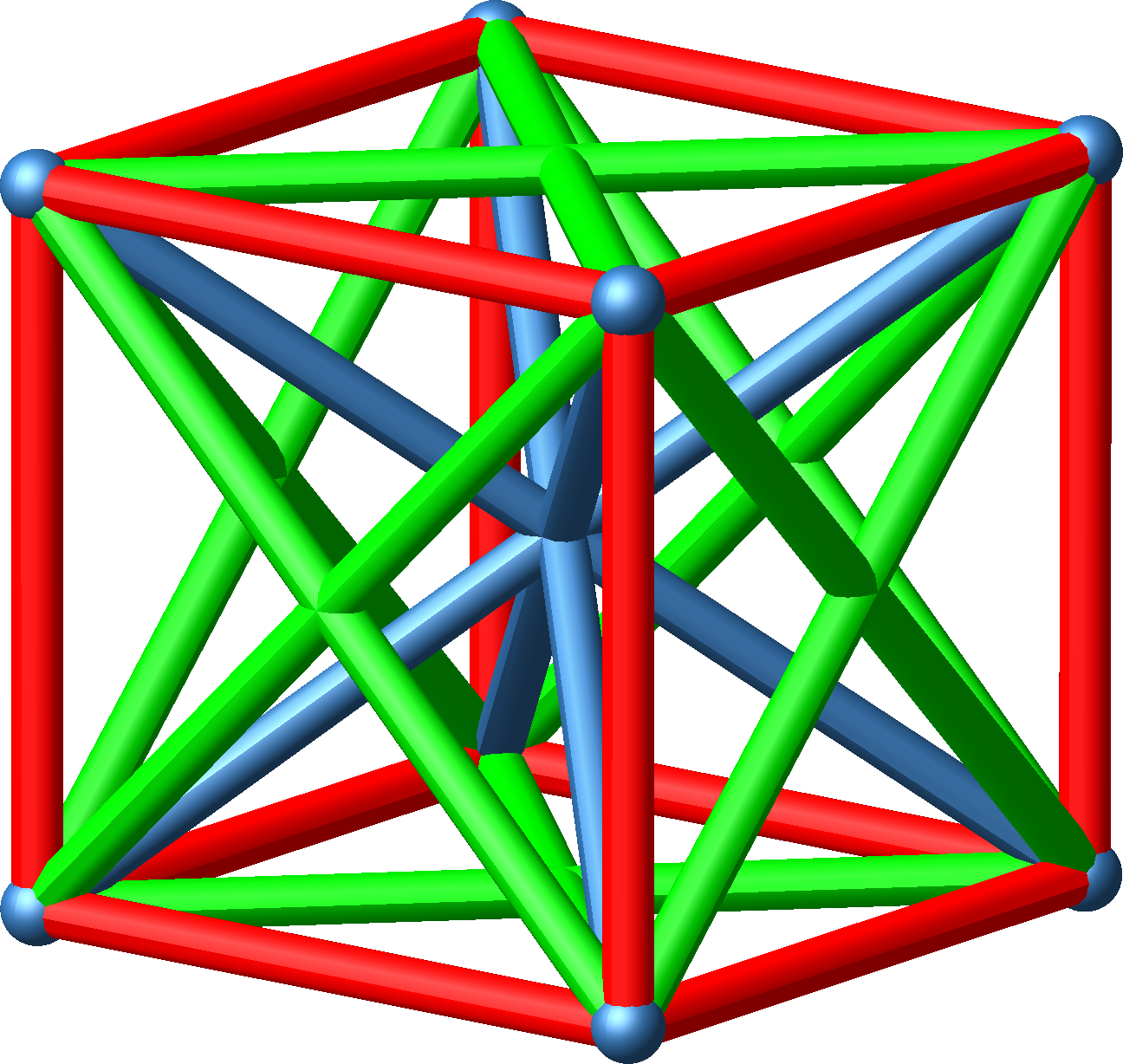
Ein Bild, das farbig, Briefpapier, Schreibgerät, rot enthält. Automatisch generierte Beschreibung

Abb. 4.4: Vollständige Darstellung

Längenverhältnis = 1 : √2 : √3

2.5     Dodekaeder

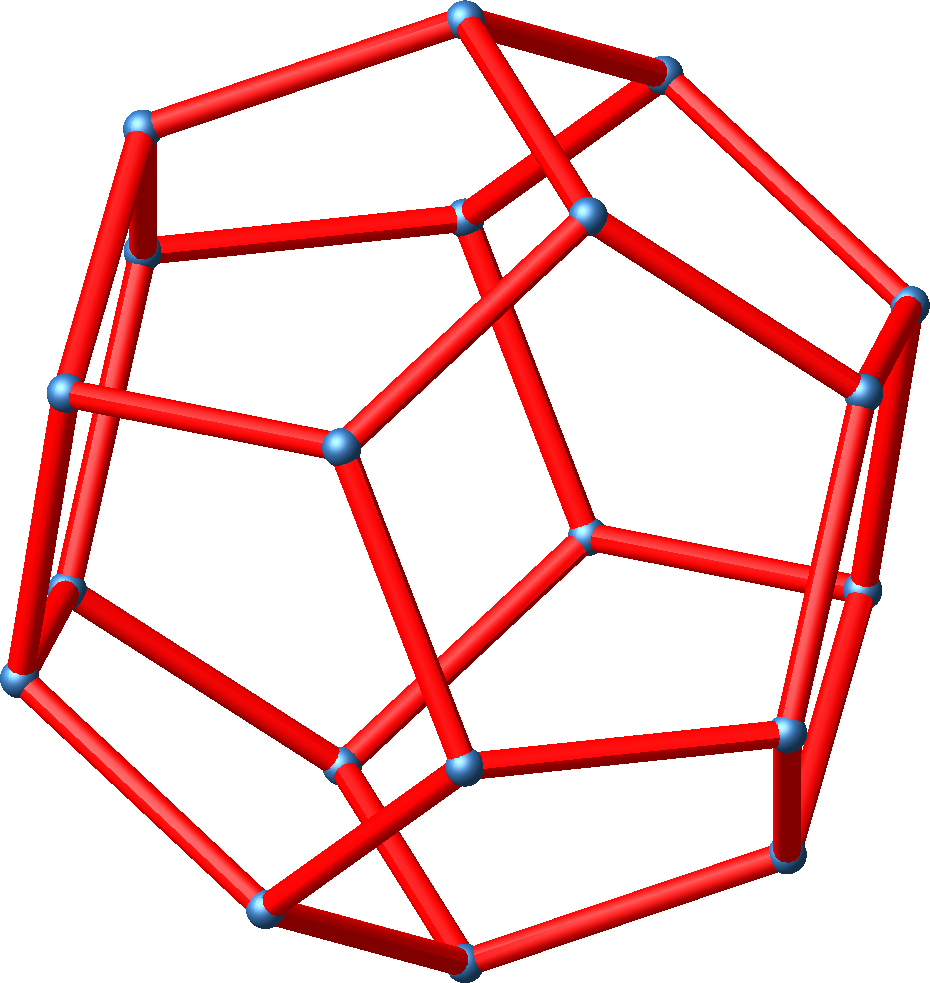
Abb. 5.1: Dodekaeder

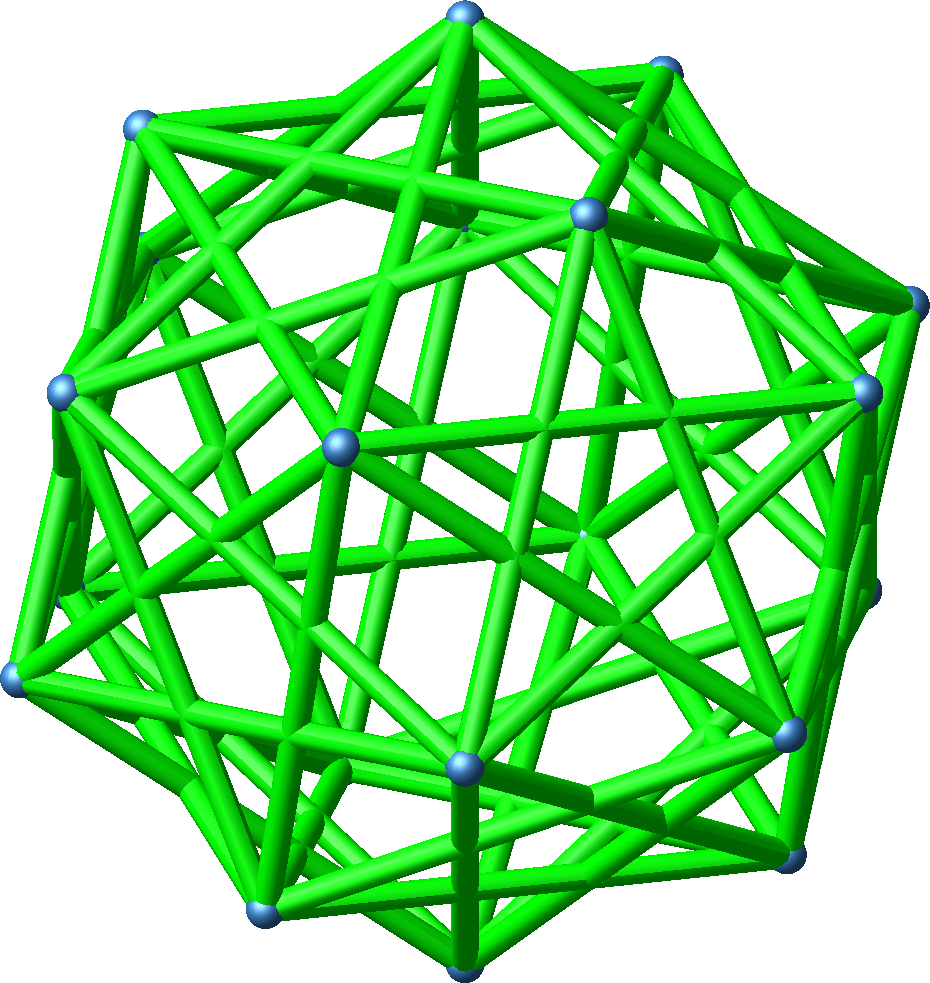
Ein Bild, das Container, Sportwettkampf, Sport, Korb enthält. Automatisch generierte Beschreibung

Abb. 5.2: Seitenflächendiagonalen

Ein Bild, das Stuhl, Container enthält. Automatisch generierte Beschreibung

Abb. 5.3: Weitere Diagonalen

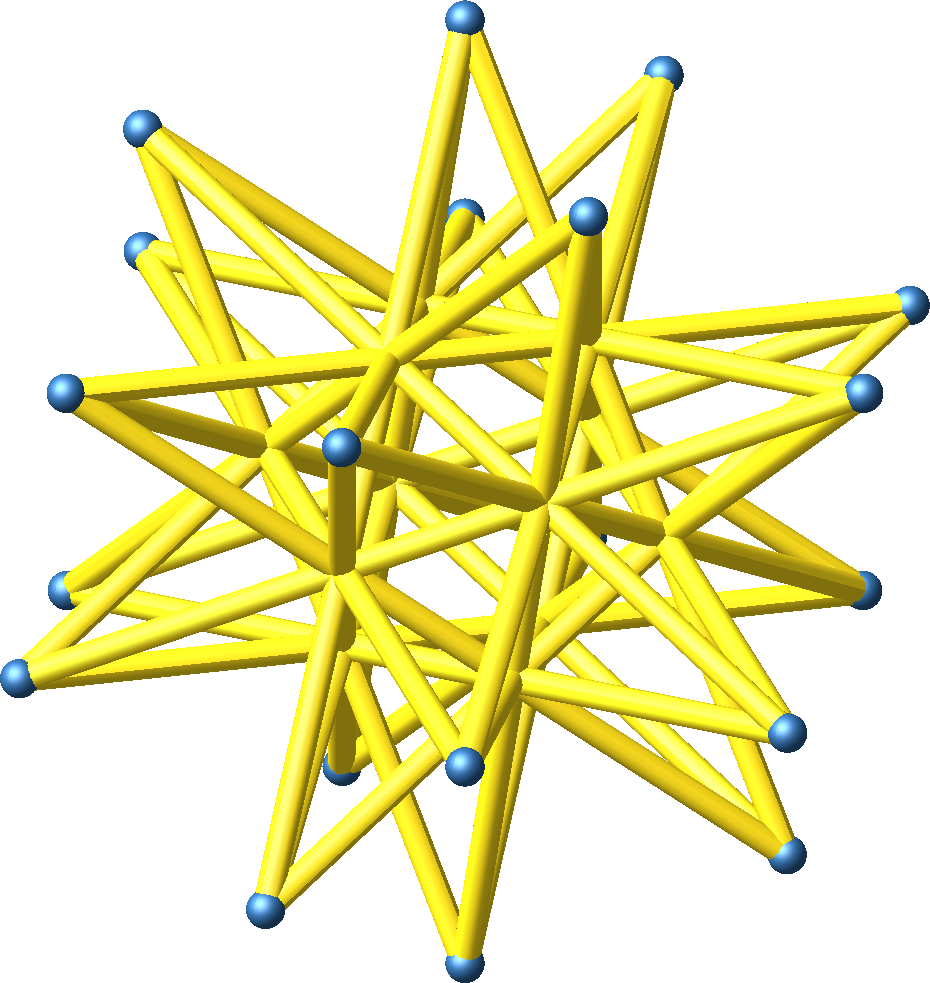
Abb. 5.4: Ikosaederstern

Der Ikosaederstern (Abb. 5.4) ist ein Kepler-Poinsot-Körper. Er besteht aus einem Ikosaeder mit 20 aufgesetzten Dreikant-Pyramiden.

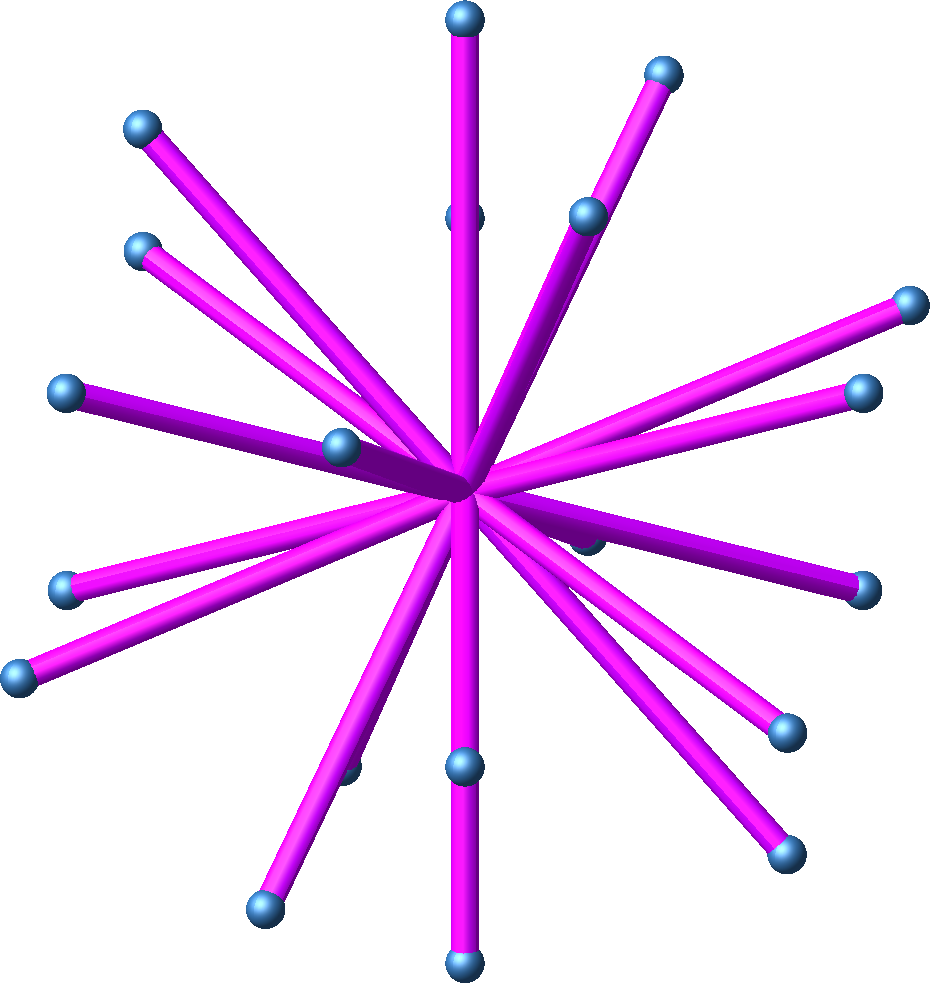
Ein Bild, das Schreibgerät, Bleistift enthält. Automatisch generierte Beschreibung

Abb. 5.5: Mittelpunktsdiagonalen

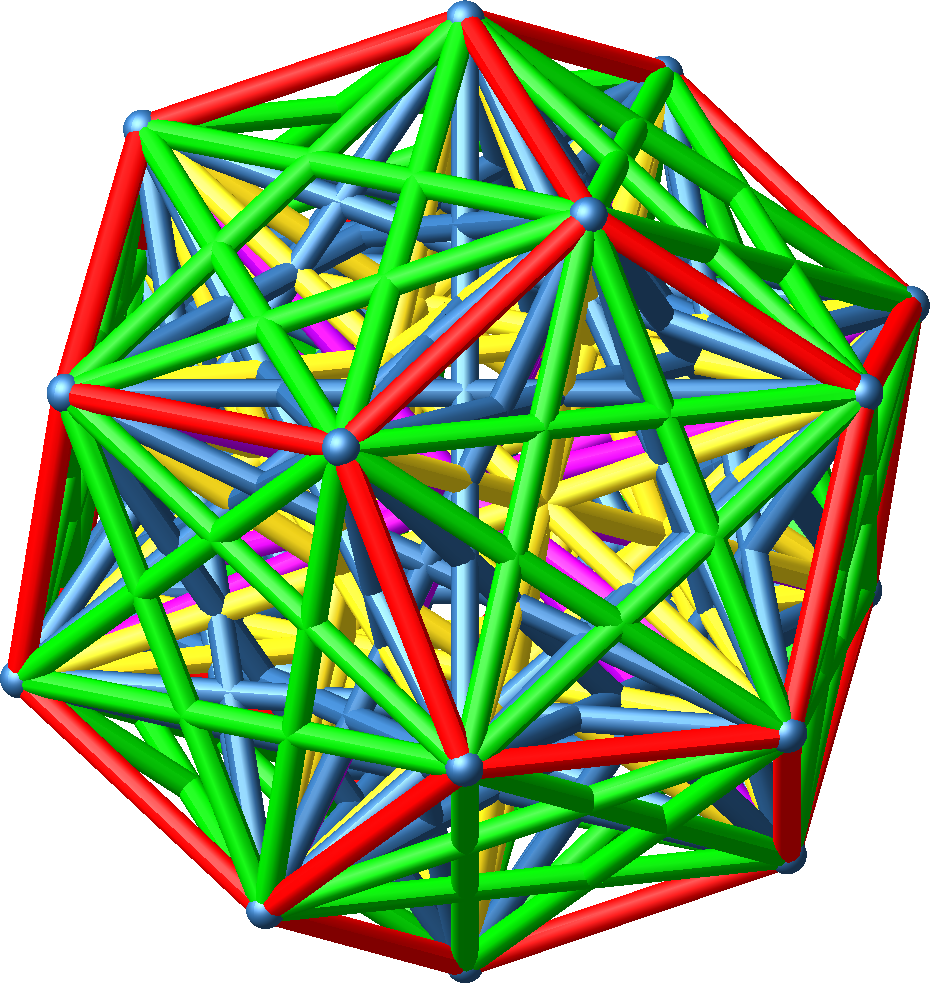
Abb. 5.6: Vollständige Darstellung

Längenverhältnis = ϕ : 1 : √2 : Φ : √3

 

 

Weblinks

Hans Walser: Goldene Pyramiden

http://www.walser-h-m.ch/hans/Miniaturen/G/Goldene_Pyramiden/Goldene_Pyramiden.htm

 

 

Literatur

Walser, Hans (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wußing über populärwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.