Hans Walser, [20220903]
Diagonalen im Hyperwürfel
1 Worum geht es?
Wie viele Diagonalen, sortiert nach Länge, gibt es im n-dimensionalen Hyperwürfel?
Anklänge an das Pascalsche Zahlendreieck der Binomialkoeffizienten
Schöne Bildchen
2 Quadrat
Das Quadrat hat vier Ecken, vier Kanten (Seiten) der Länge 1 und zwei Diagonalen der Länge √2 (Abb. 1).
Liste: 4, 4, 2

Abb. 1: Quadrat
3 Würfel
Der Würfel hat acht Ecken, zwölf Kanten der Länge 1, zwölf Seitenflächendiagonalen der Länge √2 und vier Raumdiagonalen der Länge √3 (Abb. 2).
Liste: 8, 12, 12, 4
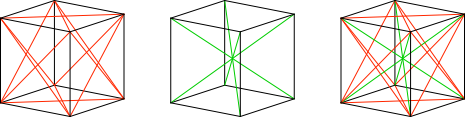
Abb. 2: Würfel
Die Abbildung 3 zeigt den Würfel mit den Diagonalen in isometrischer Darstellung. Dabei werden alle Würfelkanten gleich verkürzt dargestellt. Allerdings ist die Verkürzung bei den verschiedenen Diagonalen ungleich. Zudem stimmen in der Abbildung 3 die vorne-hinten-Relationen nicht. Dies ist technisch durch den Zeichenalgorithmus bedingt.
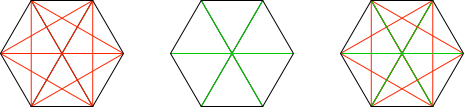
Abb. 3: Isometrische Darstellung
Wir werden faute de mieux für die Hyperwürfel ebenfalls die isometrische Darstellung verwenden.
4 Vierdimensionaler Hyperwürfel
Der vierdimensionale Hyperwürfel (Abb. 4.1) hat 16 Ecken und 32 Kanten der Länge 1.
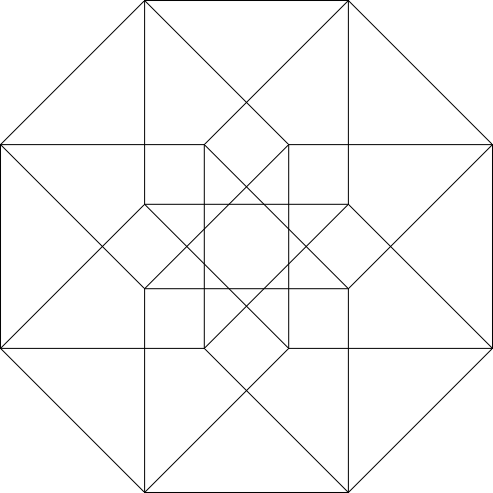
Abb. 4.1: Vierdimensionaler Hyperwürfel
Er hat 48 Diagonalen der Länge √2. In der Abbildung 4.2 überdecken sie sich teilweise.
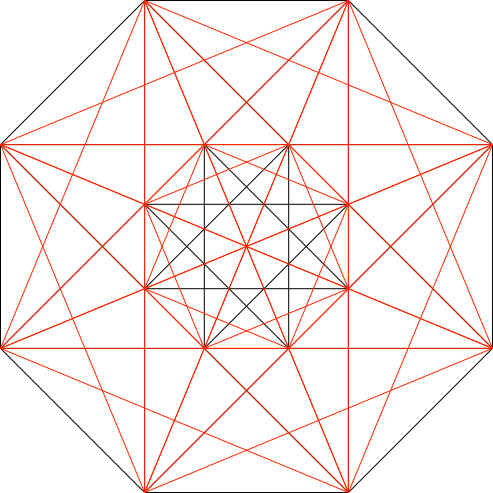
Abb. 4.2: 48 Diagonalen der Länge √2
Weiter gibt es 32 Diagonalen der Länge √3 (Abb. 4.3).
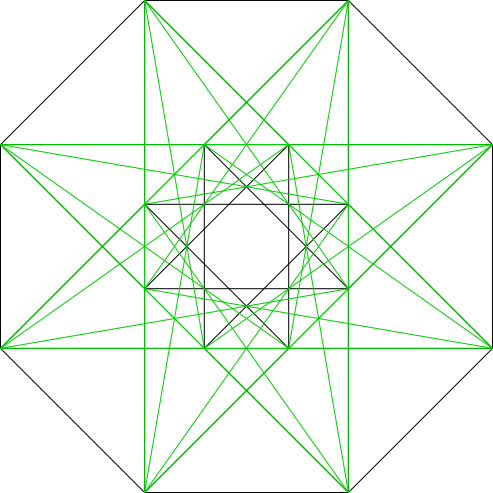
Abb. 4.3: 32 Diagonalen der Länge √3
Und schließlich 8 Diagonalen der Länge √4 = 2 (Abb. 4.4).
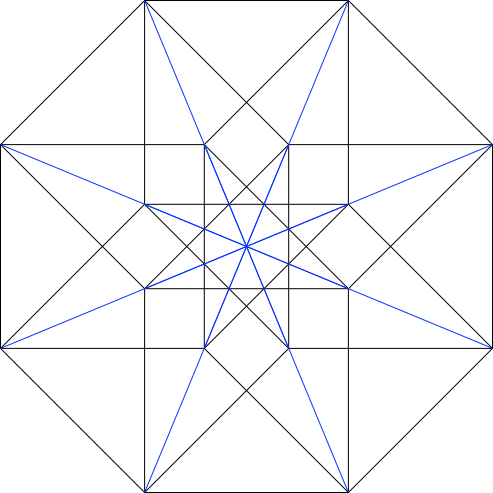
Abb. 4.4: 32 Diagonalen der Länge √4
Die Abbildung 4.5 zeigt, soweit nicht verdeckt, alle Diagonalen des vierdimensionalen Hyperwürfels.
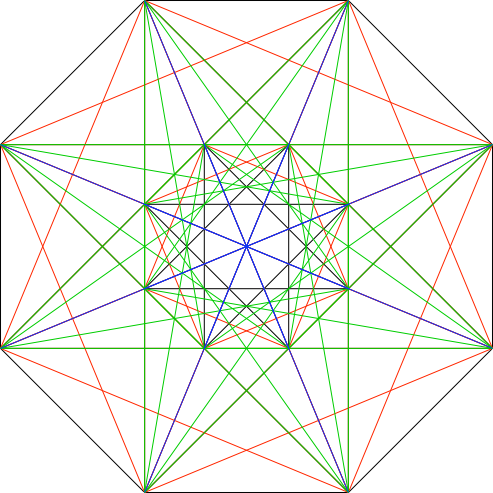
Abb. 4.5: Alle Diagonalen
Liste: 16, 32, 48, 32, 8
5 Dimension fünf
Die Abbildungen 5 zeigen das entsprechende Spielchen für den fünfdimensionalen Hyperwürfel.
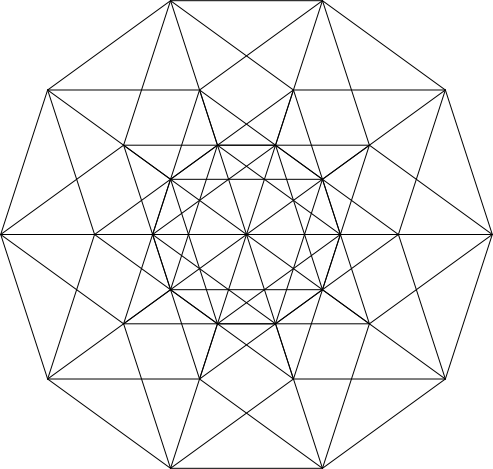
Abb. 5.1: Fünfdimensionaler Hyperwürfel mit 32 Ecken und 80 Kanten

Abb. 5.2: 160 Diagonalen der Länge √2

Abb. 5.3 160 Diagonalen der Länge √3

Abb. 5.4: 80 Diagonalen der Länge √4
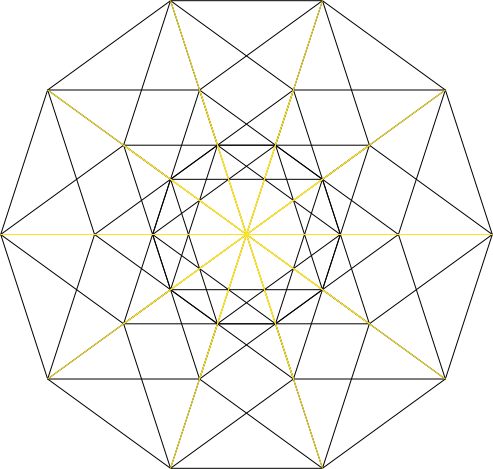
Abb. 5.5: 16 Diagonalen der Länge √5

Abb.
5.6: Alle Diagonalen
Liste:
32, 80, 160, 160, 80, 16
6
Sechsdimensionaler Hyperwürfel
Liste : 64,
192, 480, 640, 480, 192, 32

Abb. 6:
Sechsdimensionaler Hyperwürfel mit allen Diagonalen
7
Anzahlen
der Diagonalen
Die Tabelle 1 gibt
eine Übersicht.
|
|
Eckpunkte |
Kanten |
Diagonalen |
Diagonalen |
Diagonalen |
Diagonalen |
Diagonalen |
|
Länge |
0 |
1 |
√2 |
√3 |
√4 |
√5 |
√6 |
|
Farbe |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dimension |
|
|
|
|
|
|
|
|
0 |
1 |
|
|
|
|
|
|
|
1 |
2 |
1 |
|
|
|
|
|
|
2 |
4 |
4 |
2 |
|
|
|
|
|
3 |
8 |
12 |
12 |
4 |
|
|
|
|
4 |
16 |
32 |
48 |
32 |
8 |
|
|
|
5 |
32 |
80 |
160 |
160 |
80 |
16 |
|
|
6 |
64 |
192 |
480 |
640 |
480 |
192 |
32 |
Tab.
1: Anzahlen der Diagonalen
Die Anzahlen können
mit einer geeigneten Zweierpotenz ( (½)Dimension–1) skaliert werden
(Tab. 2). Es erscheinen die Binomialkoeffizienten, in der ersten Spalte
allerdings verdoppelt.
|
|
Eckpunkte |
Kanten |
Diagonalen |
Diagonalen |
Diagonalen |
Diagonalen |
Diagonalen |
|
Länge |
0 |
1 |
√2 |
√3 |
√4 |
√5 |
√6 |
|
Farbe |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dimension |
|
|
|
|
|
|
|
|
0 |
2 |
|
|
|
|
|
|
|
1 |
2 |
1 |
|
|
|
|
|
|
2 |
2 |
2 |
1 |
|
|
|
|
|
3 |
2 |
3 |
3 |
1 |
|
|
|
|
4 |
2 |
4 |
6 |
4 |
1 |
|
|
|
5 |
2 |
5 |
10 |
10 |
5 |
1 |
|
|
6 |
2 |
6 |
15 |
20 |
15 |
6 |
1 |
Tab. 2: Skalierte
Tabelle