Hans Walser, [20170421]
Diagonalenschnittpunkte in regelm§igen Vielecken
1 Worum geht es?
Es wird eine Vermutung ber die Schnittpunkte von Diagonalen in regelm§igen Vielecken ungerader Eckenzahl formuliert.
2 Terminologie
Eine Punkt durch welchen n Geraden verlaufen nennen wir einen Schnittpunkt n-ten Grades.
Die klassischen Schnittpunkte der Dreiecksgeometrie (Hhenschnittpunkt, Schwerlinienschnittpunkt, Mittelsenkrechtenschnittpunkt, Winkelhalbierendenschnittpunkt) sind Schnittpunkte dritten Grades.
3 Vielecke ungerader Eckenzahl
Wir zeichnen smtliche Diagonalen in Vielecken ungerader Eckenzahl. Die Abbildung 1 zeigt die Situation fr die Eckenzahlen 3 bis 13.
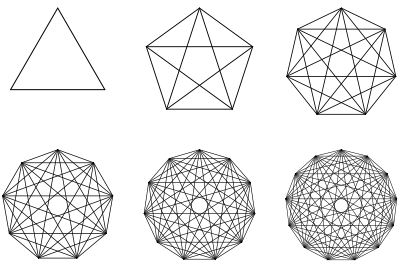
Abb. 1: Diagonalen
Im Innern der Vielecke nur Schnittpunkte zweiten Grades.
Im Folgenden weitere Beispiele.
Im regelm§igen 15-Eck (Abb. 2) hat es zwar Diagonalenschnittpunkte zweiten Grades, die sehr nahe beieinander liegen. Aus Symmetriegrnden kann aber ausgeschlossen werden, dass sie aufeinander fallen. Wir haben also nur Schnittpunkte zweiten Grades.
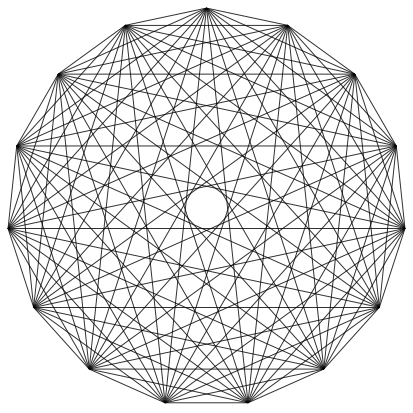
Abb. 2: Regelm§iges 15-Eck
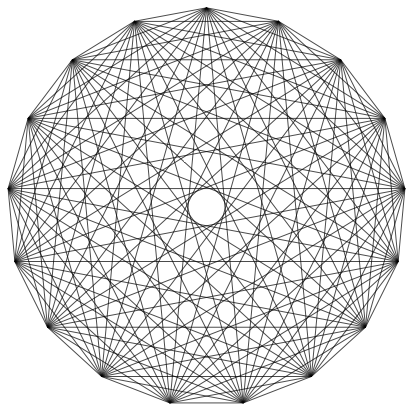
Abb. 3a: Regelm§iges 17-Eck
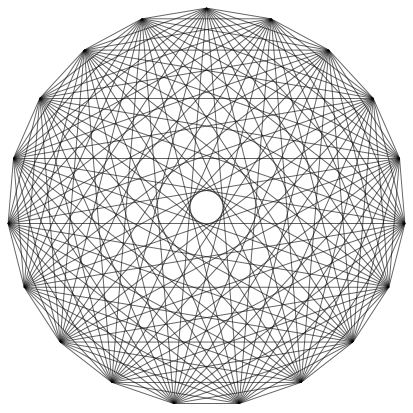
Abb. 3b: Regelm§iges 19-Eck
Im regelm§igen 27-Eck der Abbildung 4 sind einige ãfastÒ-Beispiele von Schnittpunkten hheren Grades suggeriert. Sie erweisen sich bei nherem Hinsehen alle als falsch.

Abb. 4: Falsche Beispiele im 27-Eck
3.1 Vermutung
Im Innern eines Vieleckes mit ungerader Eckenzahl gibt es keinen Punkt der von mehr als zwei Diagonalen getroffen wird. Es gibt nur Diagonalenschnittpunkte zweiten Grades.
4 Gerade Eckenzahlen
Es sei n= 2m die Eckenzahl.
Fr allfllige Berechnungen setzen wir den Umkreisradius 1.
4.1 Mittelpunkt
Der Mittelpunkt wird von den m Mittelpunktsdiagonalen getroffen. Fr m ³ 3 haben wir also als Mittelpunkte einen Schnittpunkt m-ten Grades (Abb. 5 fr m = 3).

Abb. 5: Mittelpunkt
4.2 Diagonalenschnittpunkte au§erhalb des Mittelpunktes
4.2.1 Regelm§iges Achteck
Im Innern des regelm§igen Achteckes (Abb. 6a) haben wir acht Schnittpunkte dritten Grades. Da eine der drei beteiligten Diagonalen auch Symmetrieachse ist, ist die Schnittpunkteigenschaft trivial.
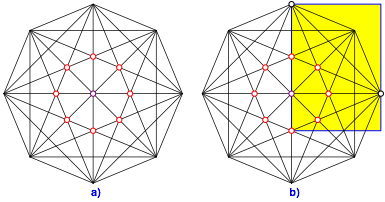
Abb. 6: Im Achteck
Diese Schnittpunkte haben vom Mittelpunkt den Abstand:
![]() (1)
(1)
Diese Lngen erscheinen in der Geometrie des DIN-Formates (Walser 2013b). Wir knnen ein Rechteck im DIN-Format einpassen (Abb. 6b).
4.2.2 Regelm§iges Zehneck
Im regelm§igen Zehneck gibt es ebenfalls Schnittpunkte dritten Grades (Abb. 7a). Die Schnittpunkteigenschaft ist aus Symmetriegrnden klar.
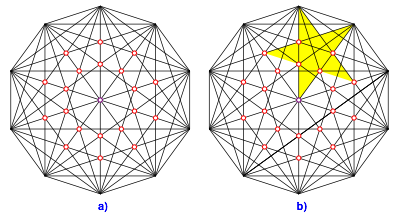
Abb. 7: Im Zehneck
Die zehn Schnittpunkte des inneren Kranzes haben vom Mittelpunkt den Abstand:
![]() (2)
(2)
Dabei bezeichnen wir mit
![]() (3)
(3)
den so genannten Goldenen Schnitt (Walser 2013a, S. 16).
Die Schnittpunkte des u§eren Kranzes haben vom Mittelpunkt den Abstand:
![]() (4)
(4)
Die Punkte teilen also die Radiusstrecke im Verhltnis des Goldenen Schnittes. Wer htte das gedacht! Wir knnen also ein Pentagramm einpassen (Abb. 7b).
4.2.3 Regelm§iges Zwlfeck
Im regelm§igen Zwlfeck wird es spannend (Abb. 8).
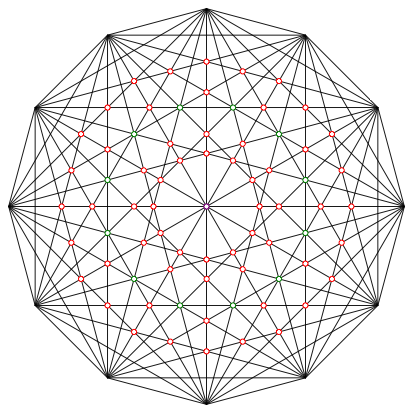
Abb. 8: Im regelm§igen Zwlfeck
Wir haben insgesamt fnf Krnze von Schnittpunkten dritten Grades (rot) und einen Kranz von Schnittpunkten vierten Grades (grn). Wir besprechen das im Einzelnen.
Der innerste Kranz von roten Punkten hat vom Mittelpunkt einen Abstand:
![]() (5)
(5)
Der zweitinnerste Kranz roter Punkte hat vom Mittelpunkt den Abstand:
![]() (6)
(6)
Der dritte Kranz roter Punkte hat den Radius:
![]() (7)
(7)
4.2.3.1 Nichttriviale rote Schnittpunkte
Der vierte Kranz roter Punkte hat den Radius:
![]() (8)
(8)
Die Schnittpunkteigenschaft der roten Punkte des vierten Kranzes ist nicht trivial, da keine Mittelpunktdiagonale beteiligt ist. Um die Schnittpunkteigenschaft einzusehen, betten wir das Zwlfeck in einen Quadratraster ein (Abb. 9).
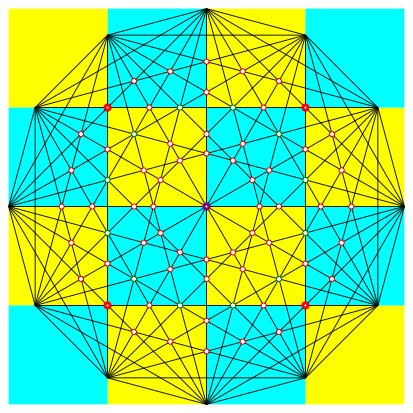
Abb. 9: Im Quadratraster
Die an den fetten roten Punkten, welche zum vierten Kranz gehren, beteiligten Zwlfeckdiagonalen sind Rasterlinien oder Diagonallinien des Rasters. Damit ist die Schnittpunkteigenschaft nachgewiesen. Zugleich wir klar, warum beim Abstand vom Mittelpunkt die Quadratwurzel aus 2 erscheint.
Wer der Raster-Einbettung nicht traut, kann im gelb markierten Dreieck der Abbildung 10 die Winkel-Version des Satzes von Ceva (Walser 2012, S. 145f) anwenden. Da der Fcherwinkel (Winkel zwischen aufeinanderfolgenden Diagonalen) im regelm§igen 12-Eck 15¡ betrgt, knnen die bentigten Winkel leicht abgezhlt werden.
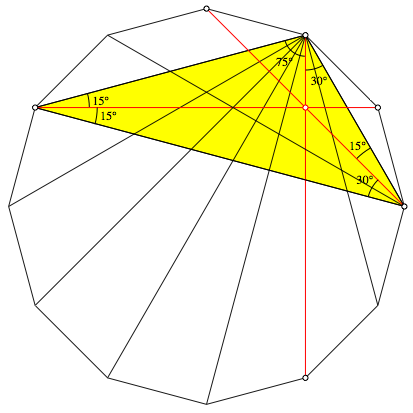
Abb. 10: Anwendung des Satzes von Ceva
Zu zeigen ist:
![]() (9)
(9)
Bearbeitung der linken Seite:
![]() (10)
(10)
Der fnfte und u§erste Kranz roter Punkte hat den Radius:
![]() (11)
(11)
Die Werte von (5) und (9) ergnzen sich auf 1.
4.2.3.2 Grne Schnittpunkte
Der Kranz der Schnittpunkte vierten Grades (grn) hat den Radius:
![]() (12)
(12)
Die Schnittpunkteigenschaft der grnen Punkte ist nicht trivial. Sie kann durch Einpassen eines Sterns in die Figur eingesehen werden (Abb. 11).
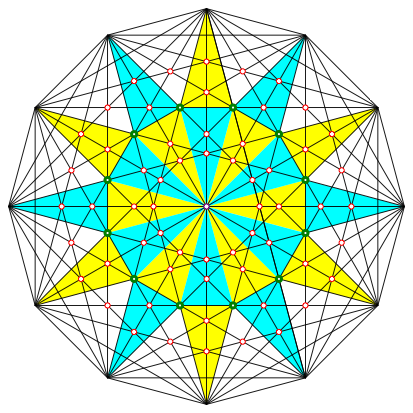
Abb. 11: Einpassen eines Sterns
Wer der Sache mit dem Stern nicht traut, kann wie folgt argumentieren. Die vier am Schnittpunkt beteiligten Diagonalen bilden eine symmetrische Figur. Die Symmetrieachse ist allerdings keine Diagonale, aber eine Symmetrieachse des regelm§igen Zwlfecks. Aus Symmetriegrnden knnen wir daher fr den Beweis der Schnittpunkteigenschaft eine der vier Diagonalen weglassen (hellgrn in Abb. 12). Die verbleibenden drei Diagonalen sind im gelb markierten Dreieck die Winkelhalbierenden.
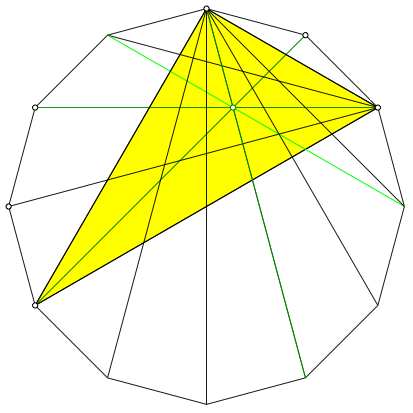
Abb. 12: Winkelhalbierende
4.2.4 Regelm§iges 14-Eck
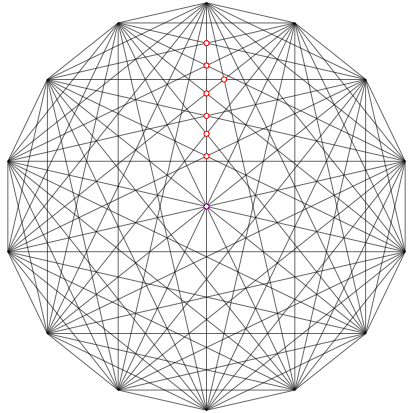
Abb. 13: Regelm§iges 14-Eck
Im 14-Eck hat es nur Schnittpunkte dritten Grades. In der Abbildung 13 ist fr jeden Kranz ein Beispiel eingezeichnet. Der einzige nichttriviale Schnittpunkt ist derjenige neben der Mittelpunktdiagonale. Der geneigte Leser ist eingeladen, die Schnittpunkteigenschaft nachzuweisn (Tipp: Trigonometrie).
4.2.5 Regelm§iges 16-Eck
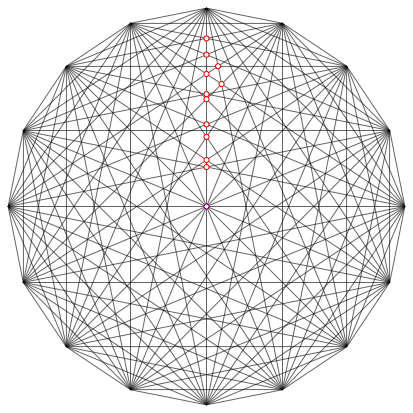
Abb. 14: Regelm§iges 16-Eck
Nur Schnittpunkte dritten Grades, davon zwei nichttriviale.
4.2.6 Regelm§iges 18-Eck
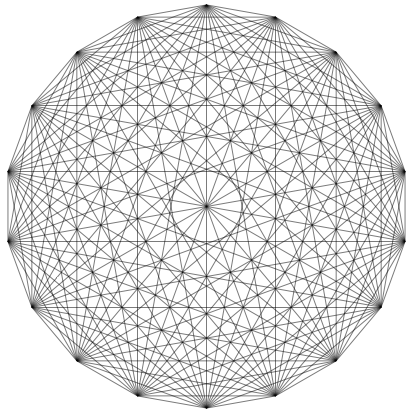
Abb. 15: Sternenhimmel
Im regelm§igen 18-Eck sehen wir Schnittpunkte dritten, vierten und fnften Grades (Abb. 15 und 16).
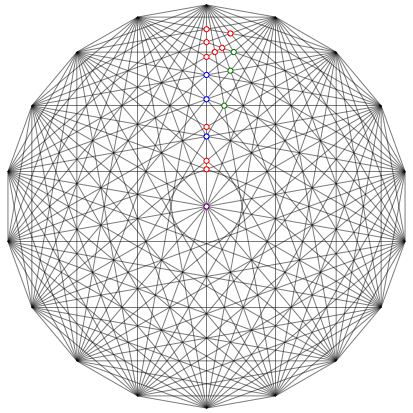
Abb. 16: Exemplarische Auswahl von Schnittpunkten
Die nichttrivialen Schnittpunkte dritten Grades sowie smtliche Schnittpunkte vierten und fnften Grades sind zu beweisen. Exemplarisch einige Beweise.
4.2.6.1 Ein nichttrivialer roter Schnittpunkt
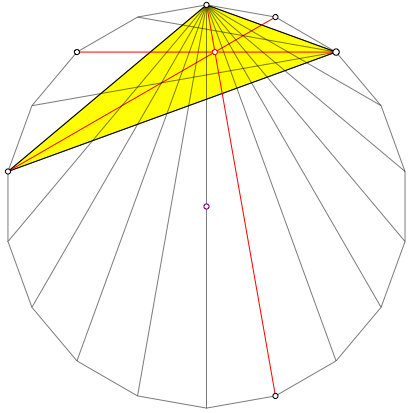
Abb. 17: Nichttrivialer roter Schnittpunkt
Der nichttriviale rote Schnittpunkt in der Abbildung 17 ist Winkelhalbierendenschnittpunkt im gelb markierten Dreieck.
4.2.6.2 Ein grner Schnittpunkt
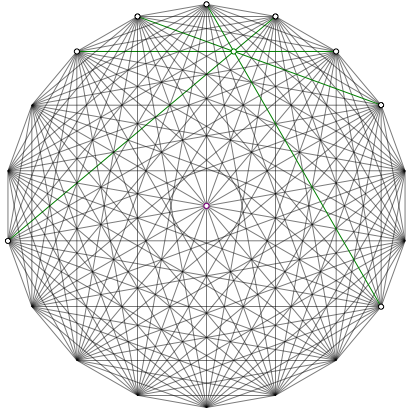
Abb. 18: Grner Schnittpunkt vierten Grades
Due vier am Schnittpunkt vierten Grades (Abb. 18) beteiligten Diagonalen bilden eine symmetrische Figur. Die Symmetrieachse ist keine Diagonale, aber eine Symmetrieachse des 18-Ecks. Aus Symmetriegrnden knnen wir daher eine der vier Diagonalen weglassen. Wir lassen die waagerechte Diagonale weg (Abb. 19).
Fr den Beweis der Schnittpunkteigenschft der drei verbleibenden Diagonalen arbeiten wir im gelb markierten Dreieck mit der Winkel-Version des Satzes von Ceva (Walser 2012, S. 145f).
Da im regelm§igen 18-Eck der Fcherwinkel (Winkel zwischen zwei benachbarten Diagonalen) 10¡ misst, knnen wir die bentigten Winkel leicht ablesen.
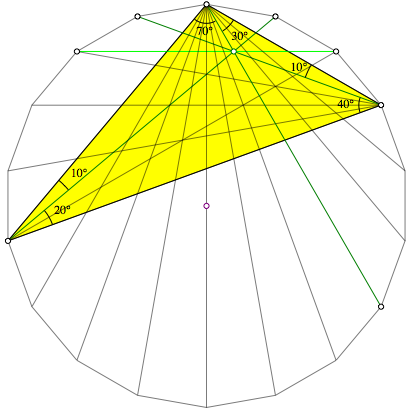
Abb. 19: Beweisfigur
Zu zeigen ist:
![]() (13)
(13)
Umformung der linken Seite gibt:
![]() (14)
(14)
Damit ist die Schnittpunkteigenschaft fr den grnen Schnittpunkt vierten Grades bewiesen.
4.2.6.3 Ein blauer Schnittpunkt
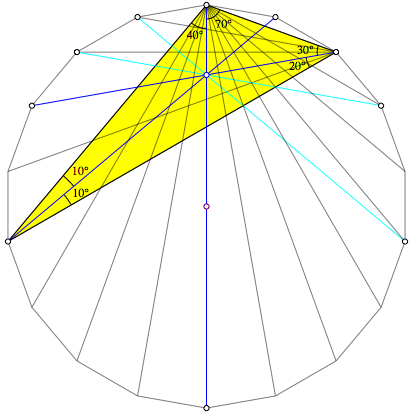
Abb. 20: Ein blauer Schnittpunkt
Die fnf an einem blauen Schnittpunkt beteiligten Diagonalen bilden eine symmetrische Figur mit einer Mittelpunktdiagonalen als Symmetrieachse. Aus Symmetriegrnden knnen wir daher die beiden in der Abbildung 20 hellblau gezeichneten Diagonalen fr die berlegung weglassen.
Fr die dunkelblau gezeichneten Diagonalen wenden wir wiederum die Winkel-Version des Satzes von Ceva an. Zu zeigen ist:
![]() (15)
(15)
Dies ist identisch mit (13) und wurde in (14) nachgewiesen. Die beiden gelben Dreiecke der Abbildungen 19 und 20 sind aber nicht kongruent oder hnlich, da die Teilwinkel ungleich angeordnet sind.
4.2.6.4 Problemlsen
Das regelm§ige 18-Eck ist ein beliebtes Tummelfeld fr Problemlseaufgaben. Das 18-Eck tritt dabei nicht explizit auf, ist aber der Schlssel zur Lsung. Der vermeintliche Schwierigkeitsgrad liegt darin, dass das regelm§ige 18-Eck nicht mit Zirkel und Lineal konstruierbar ist und daher einen gewissen Tabucharakter hat. Beispiele dazu.
Literatur
Walser, Hans (2012): 99 Schnittpunkte. Beispiele – Bilder – Beweise. 2. Auflage. EAGLE, Edition am Gutenbergplatz: Leipzig. ISBN 978-3-937219-95-0.
Walser, Hans (2013a): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wu§ing ber populrwissenschaftliche Mathematikliteratur aus Leipzig. Edition am Gutenbergplatz, Leipzig. ISBN 978-3-937219-85-1.
Walser, Hans (2013b): DIN A4 in Raum und Zeit. Silbernes Rechteck – Goldenes Trapez – DIN-Quader. Edition am Gutenbergplatz, Leipzig 2013. ISBN 978-3-937219-69-1.
Websites
Hans Walser: 18-Eck (23.04.2017):
http://www.walser-h-m.ch/hans/Miniaturen/1/18-Eck/18-Eck.htm