1 Worum geht es?

Unter welchen Winkeln scheiden sich die Mittelpunktsdiagonalen in einem n-d-Hyperwürfels?

2 Beispiele

Die beiden Diagonalen eines Quadrates sind orthogonal.

Die vier Raumdiagonalen eines Würfels (Abb. 1) schneiden sich paarweise unter dem spitzen Winkel :

(1)

Abb. 1: Raumdiagonalen des Würfels

Spannend wird es im 4d-Raum. Die acht Mittelpunktsdiagonalen haben die Richtungsvektoren:

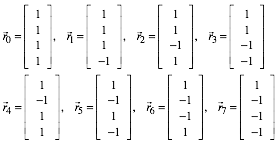(2)

Damit wird zum Beispiel:

(3)

(4)

(5)

Der spitze Winkel bei (5) ist also 60°.

Im 4d-Hyperwürfel kommen also zwei verschiedene Schnittwinkel vor.

3 Die Hamming-Distanz

Die Komponenten der Vektoren und unterscheiden sich an genau einer Stelle. Geometrisch heißt das, dass die zugehörigen Eckpunkte des 4d-Hyperwürfels durch genau eine Kante verbunden sind. Sie haben die Hamming-Distanz 1. Die zugehörigen Mittelpunktsdiagonalen schneiden sich unter 60°.

Die Komponenten der Vektoren und unterscheiden sich an genau zwei Stellen. Geometrisch heißt das, dass ein Kantenweg von einem Eckpunkt zum anderen über zwei Kanten verläuft (es gibt zwei solche Kantenwege). Die beiden Eckepunkte haben die Hamming-Distanz 2 (die euklidische Distanz ist ). Die zugehörigen Mittelpunktsdiagonalen sind orthogonal.

Wir sehen, wie der Hase läuft.

4 Allgemeine Formel

Für zwei Mittelpunktsdiagonalen im n-d-Hyperwürfel, deren Endpunkte die Hamming-Distanz d haben, ergibt sich der spitze Schnittwinkel :

(6)

5 Tabelle

Die Tabelle 1 zeigt einige Werte.

n\d	1	2	3	4	5	6	7	8
2	90
3	70.5288
4	60	90
5	53.1301	78.4630
6	48.1897	70.5288	90
7	44.4153	64.6231	81.7868
8	41.4096	60	75.5225	90
9	38.9424	56.2510	70.5288	83.6206
10	36.8699	53.1301	66.4218	78.4630	90
11	35.0968	50.4788	62.9643	74.1734	84.7841
12	33.5573	48.1897	60	70.5288	80.4059	90
13	32.2042	46.1869	57.4210	67.3801	76.6576	85.5883
14	31.0027	44.4153	55.1501	64.6231	73.3985	81.7868	90
15	29.9264	42.8334	53.1301	62.1819	70.5288	78.4630	86.1774
16	28.9550	41.4096	51.3178	60	67.9757	75.5225	82.8192	90

Tab. 1: Schnittwinkel