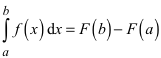Hans Walser, [20230404]

Differenzen

1 Worum geht es?

Spiel im Pascal-Dreieck der Binomialkoeffizienten

2 Pascal-Dreieck

Die Abbildung 1 zeigt das Pascal-Dreieck der Binomialkoeffizienten in einem Sechseckraster.

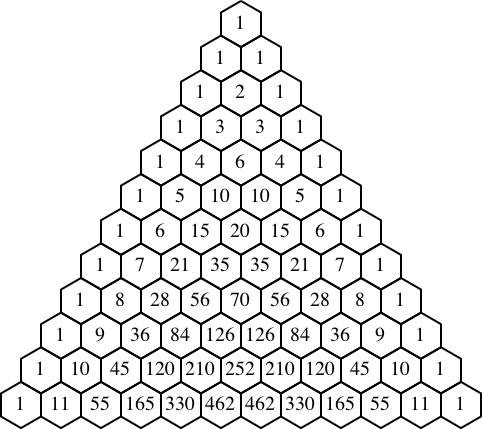
Abb. 1: Pascal-Dreieck der Binomialkoeffizienten

3 Beispiele

In den folgenden Beispielen ist jeweils die Summe der Zahlen in den gelb markierten Sechsecken gleich der Differenz der Zahl im rot markierten Sechseck minus der Zahl im grün markierten Sechseck.

Die Abbildung 2 illustriert eigentlich nur ein Weiterzählen von 5 bis 9.

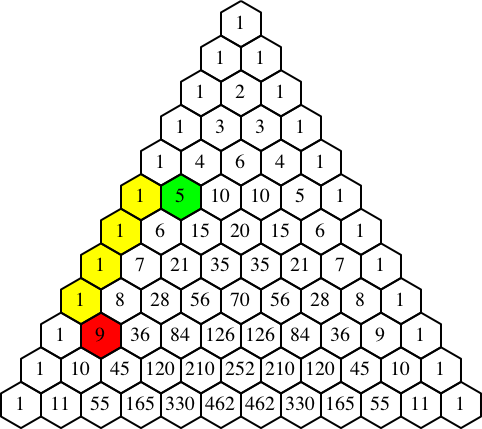
Abb. 2: 1 + 1 + 1 + 1 = 9 – 5

Im Beispiel der Abbildung 3 ist die Sache nicht mehr sofort einsichtig. Die gelben Sechsecke laufen parallel zur linken Kante des Dreiecks.

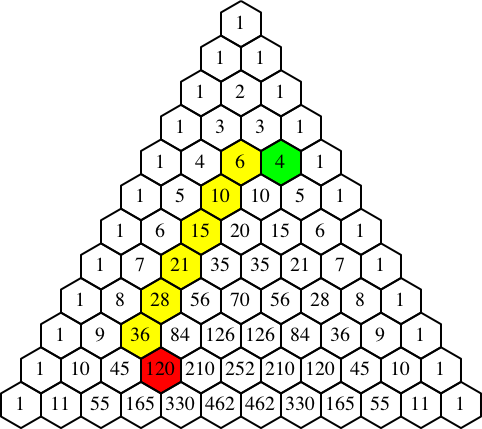
Abb. 3: 6 + 10 + 15 + 21 + 28 + 36 = 120 – 4

Das Beispiel der Abbildung 4 ist eine Umformung der Rekursionsformel der Binomialkoeffizienten.

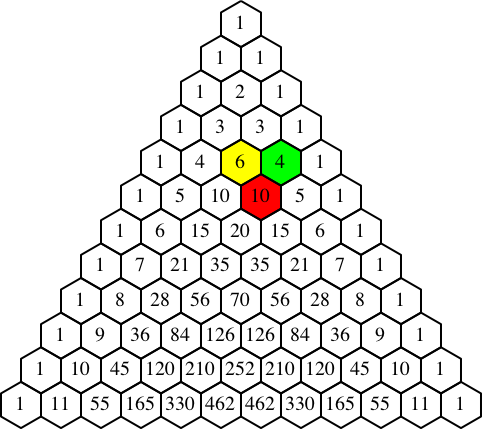
Abb. 4: 6 = 10 – 4

Im Beispiel der Abbildung 5 laufen die gelben Sechsecke parallel zur Dreieckskante rechts. Aus Symmetriegründen ist das Beispiel nicht wesentlich anders als die bisherigen Beispiele.

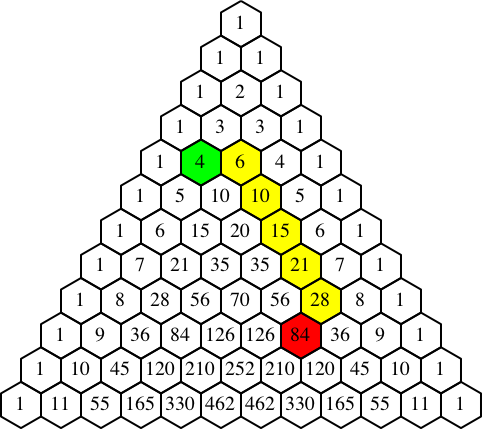
Abb. 5: 6 + 10 + 15 + 21 + 28 = 84 – 4

Wir können uns aus Symmetriegründen auf Beispiele beschränken, in denen die gelben Sechsecke parallel zur linken Dreieckskante laufen.

4 Geometrie der Figur

Wir haben eine Folge von gelb markierten Sechsecken, welche linear und parallel zur linken Kante des Pascal-Dreiecks der Binomialkoeffizienten angeordnet sind. Das Sechseck rechts neben dem obersten gelben Sechseck markieren wir grün. Das Sechseck rechts unter dem untersten gelben Sechseck markieren wir rot.

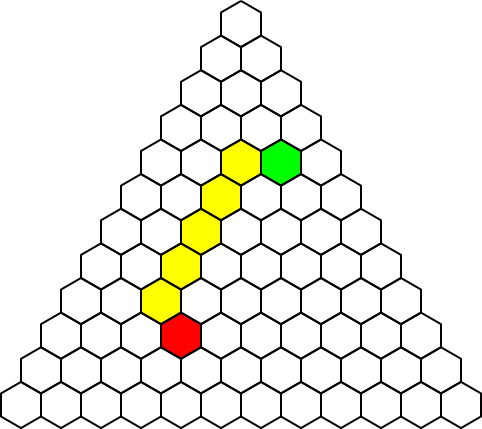
Abb. 6: Geometrie der Figur

5 Ende minus Anfang

Die Summe der Binomialkoeffizienten in den gelb markierten Feldern ist gleich dem Binomialkoeffizient im rot markierten Feld minus dem Binomialkoeffizienten im grün markierten Feld.

Didaktische Zwischenbemerkung: Es gibt viele Beispiele in der Mathematik, in welchen geeignete Werte an den Grenzen die kumulative oder integrative Berechnung von Werten zwischen den Grenzen erlauben. Das wohl bekannteste Beispiel ergibt sich aus dem Hauptsatz der Differential- und Integralrechnung. In der üblichen Schreibweise:

Das Ausweichen aus der Linie der gelb markierten Sechseck entspricht offenbar dem Bilden der Stammfunktion (Schülersprache: „Aufleiten“).

6 Beweis

Beweis induktiv nach der Länge der Folge der gelb markierten Sechsecke.

Für ein einzelnes gelb markiertes Sechseck (Abb. 4) ist die Aussage gleichwertig zur Rekursionsformel der Binomialkoeffizienten.

Angenommen, die Aussage stimmt für n gelb markierte Sechsecke (Abb. 7a für n = 4).

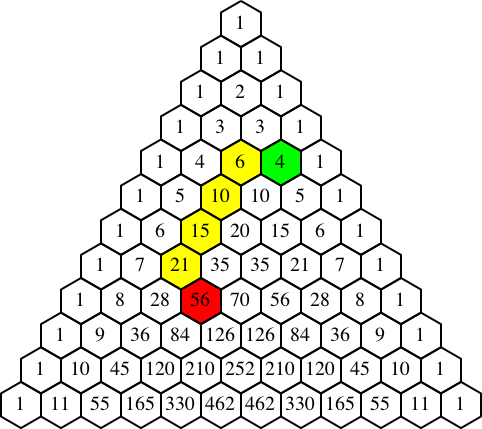
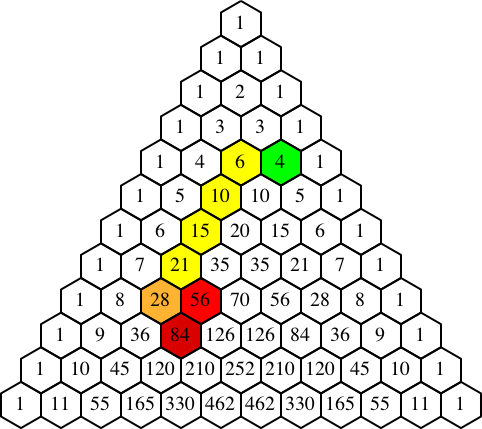
Abb. 7: Induktionsannahme und Induktionsschritt

Nun nehmen wir ein weiteres gelb markiertes Sechseck dazu (golden markiert in Abb. 7b). Nach der Rekursionsformel der Binomialkoeffizienten ist dann die Zahl im Sechseck rechts unter dem neuen gelb-goldenen Sechseck (dunkelrot in Abb. 7b) die Summe der Zahlen im vorher untersten gelb markierten und im bisher rot markierten Sechseck. Damit ist aber die Differenz zwischen der Zahl im dunkelrot markierten Sechseck und der Zahl im grün markierten Sechseck um genau die Zahl im neu dazu gekommenen gelb-goldenen Sechseck größer geworden. Die neue Summe entspricht also der neuen Differenz.

Die Abbildung 8 zeigt eine Animation des Induktionsbeweises.

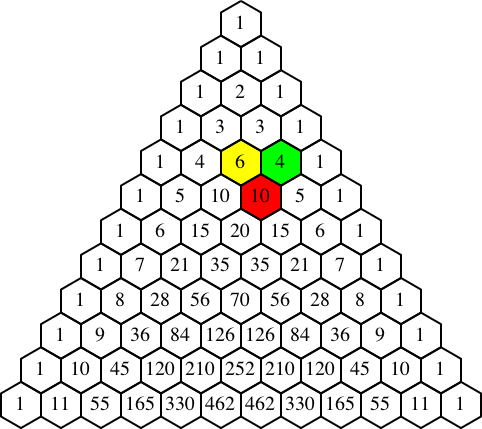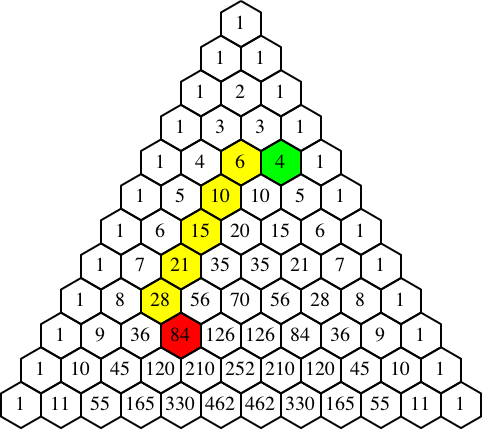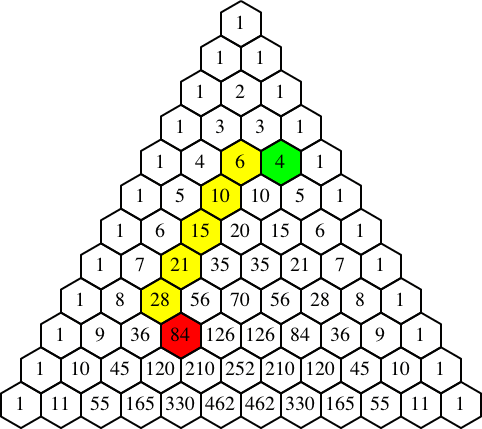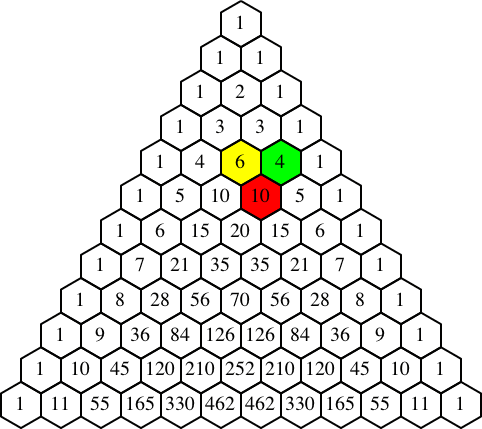
Abb. 8: Induktionsbeweis

7 Sonderfall

Wenn das oberste gelbe Sechseck an den rechten Rand des Pascal-Dreieckes anstößt (Abb. 9a), kommt das grüne Sechseck ins Elend. Wir ordnen ihm die Zahl null zu.

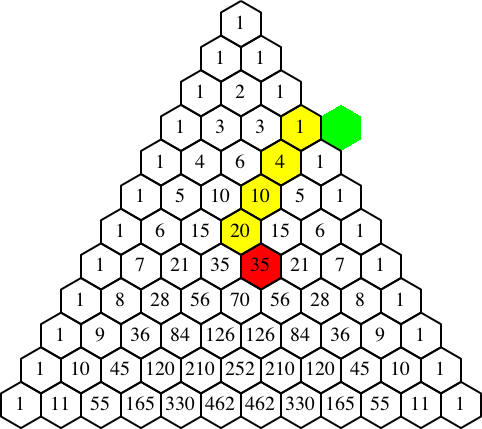
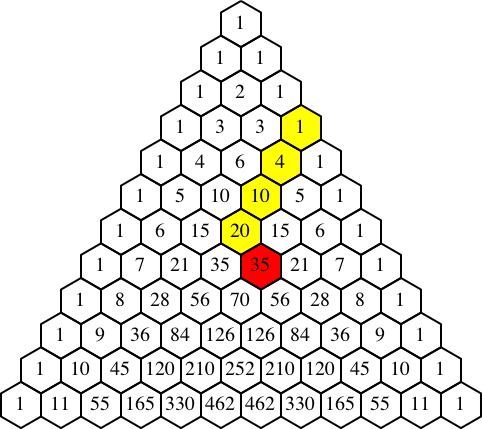
Abb. 9: Sonderfall. Socke

Unsere Regel wird noch einfacher. Die Summe der Zahlen in den gelb markierten Sechsecken ist gleich der Zahl im rot markierten Sechseck (Abb. 9b). Die gelb und rot markierten Sechsecke haben insgesamt die Form einer Socke. Daher wird dieser Sonderfall auch als „Weihnachts-Socke-Theorem“ bezeichnet (Jean Pedersen).