Hans Walser, [20161008]
Dodekaeder-Wrfel
1 About
Ein Papiermodell (Abb. 1) eines Wrfels hat enge Beziehungen zu Dodekaeder und Ikosaeder.

Abb. 1: Dodekaeder-Wrfel
2 Bauteile
Das Modell besteht aus sechs Bauteilen. Der Autor hat mit drei Farben gearbeitet, je zwei Bauteile in gleicher Farbe.
Die Abbildung 2 zeigt die Geometrie eines Bauteils. Die Abbildung 17 im Anhang zeigt dasselbe als Schnittmuster.
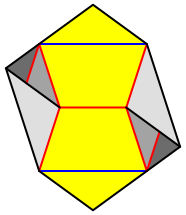
Abb. 2: Geometrie des Bauteils
Die Schnittlinien sind schwarz. Die ãTalfaltlinienÒ (konkave Faltlinien, von au§en gesehen) sind rot, die ãBergfaltlinienÒ (konvexe Faltlinien) blau eingezeichnet. Die beiden gelb markierten Fnfecke sind im fertigen Modell von au§en sichtbar. Die in Grautnen markierten Teile werden zu nicht sichtbaren Verbindungslaschen.
Da schon in den Bauteilen regelm§ige Fnfecke verwendet werden und auch weitere Winkel (36¡, 72¡, 108¡) aus dessen Umfeld erscheinen, erstaunt der Zusammenhang mit dem regelm§igen Dodekaeder nicht.
3 Schneiden der Bauteile
Wir kopieren oder ausdrucken ein Exemplar des Schnittmusters (Abb. 17), legen es auf einen Stapel von sechs farbigen Papierblttern und tackern den Stapel au§erhalb des Schnittmusterbereiches mehrfach zusammen. Dann schneiden wir den Stapel mit einem Japanmesser entlang der durchgezogenen Linien des Schnittmusters. Die gestrichelten Faltlinien dienen nur der Orientierung und sind natrlich nicht durchzuschneiden.
4 Falten der Bauteile
Auf den ausgeschnittenen farbigen Papieren fehlen die Faltlinien. Wir knnen aber trotzdem die Faltlinien akkurat anbringen wie folgt.
Die folgenden Abbildungen illustrieren den Faltvorgang mit einem Papier, das auf der Vorderseite gelb ist und auf der Rckseite hellblau. Zur Orientierung ist auch immer der Umriss des ursprnglichen Papiers angegeben.
Wir beginnen mit einem ausgeschnittenen Papier (Abb. 3a). Dann falten wir die unterste Ecke auf die oberste (Abb. 3b). Dabei achten wir darauf, dass die beiden Spickel links und rechts nicht mitgefaltet werden.
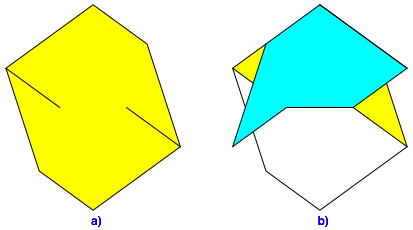
Abb. 3: Start des Faltvorganges
Wir falten auf (Abb. 4a) und falten den linken Spickel ein gem§ Abbildung 4b.
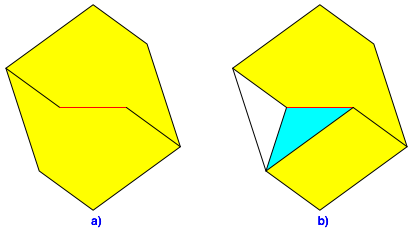
Abb. 4: Auffalten. Einfalten des linken Spickels
Ebenso falten wir den rechten Spickel ein (Abb. 5a) und falten anschlie§end den unteren Teil nach oben gem§ Abbildung 5b.
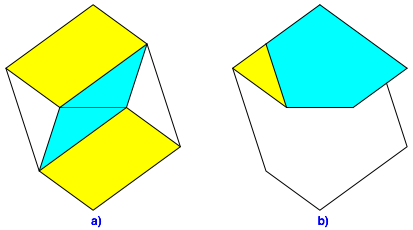
Abb. 5: Zweiten Spickel einfalten. Hochfalten
Was links vorsteht, falten wir ein (Abb. 6a), drehen die Sache um und falten wieder das Vorstehende ein (Abb. 6b). Der Papierumriss ist nun ein regelm§iges Fnfeck.
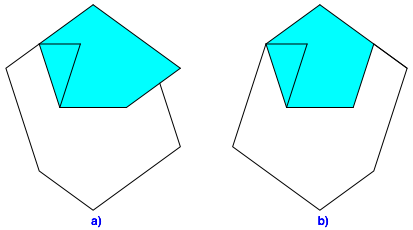
Abb. 6: Vorstehendes einfalten
Nun falten wir die vordere Giebelfront herunter (Abb. 7a), drehen um und tun dasselbe mit der zweiten Giebelfron (Abb. 7b).
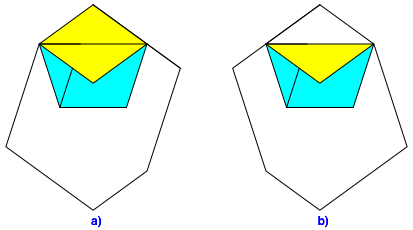
Abb. 7: Giebel herunterfalten
Jetzt falten wir alles auf (Abb. 8a) und falten noch die beiden kleinen Ecken hinein gem§ Abbildung 8b.
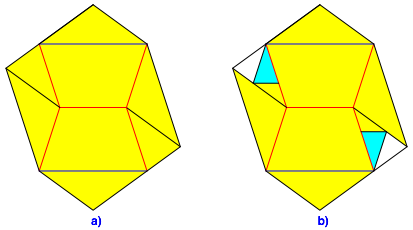
Abb. 8: Auffalten. Ecken einfalten
Der Faltvorgang ist beendet. Nun gehtÕs in den Raum. Wir falten so hoch, dass die roten Faltkanten von oben gesehen konkav werden. Die Spickel links und rechts schieben wir unter die gem§ Abbildung 8b eingefalteten Ecken.
Die Abbildung 9 zeigt das Bauteil. Das Papier ist natrlich auf beiden Seiten gelb.

Abb. 9: Bauteil
Das Bauteil ist ein umgekehrtes oder eingedrcktes Walmdach.
Die Abbildung 10 zeigt die Position des Bauteils (mit unterschiedlichen Farben auf Vorder- und Rckseite) im zuknftigen Wrfel.
Die beiden Giebeldreiecke werden beim Zusammenbau dann noch eingeklappt.
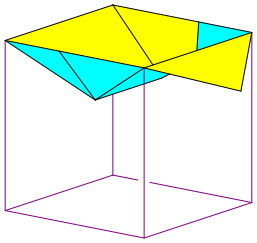
Abb. 10: Situation im Wrfel
Wir falten analog die fnf anderen Bauteile.
5 Zusammenbau
Fr den Zusammenbau orientieren wir uns an den Abbildungen 1 und 11.
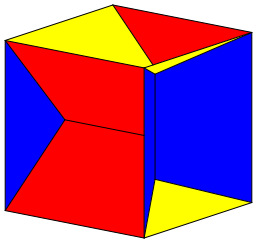
Abb. 11: Wrfel
Die Bauteile sto§en so aneinander, dass die Firstlinien der eingedrckten Walmdcher paarweise senkrecht sind.
Die Giebeldreiecke werden ber das angrenzende Bauteil geklappt. Da das Modell im Bereich der Giebeldreiecke ãdnnÒ oder ãleerÒ ist, das hei§t kein Volumen hat, knnen wir beim Zusammenbau mit Broklammern fixieren. Wenn dann alles sitzt, ersetzen wir die Broklammern mit Tackerklammern.
6 Link zum Dodekaeder
Von einem Walmdachfirst ausgehend haben wir zwei Fnfecke, die allerdings oben ber die Kante gehen. Insgesamt also zwlf Fnfecke wie beim Dodekaeder.
Das Modell hat acht Au§enecken (die Wrfelecken) und zwlf konkave Innenecken an den Enden der Firstlinien. Insgesamt also 20 Ecken wie beim Dodekaeder.
Bei den Kanten ist der Vergleich mit dem Dodekaeder nur bedingt mglich. Wir haben 30 konkave Kanten (das Dodekaeder hat 30 konvexe Kanten), aber zustzlich noch die zwlf konvexen Wrfelkanten. Da das Modell aber im unmittelbaren Anschluss an die Wrfelkanten volumenlos ist, knnen wir diese Kanten eigentlich ignorieren.
Das Modell als ganzes ist aber nicht volumenlos. Wenn wir die volumenlosen Teile wegmachen, bleibt ein Stern brig (Abb. 12). Der Stern hat acht Spitzen, ist aber nicht der Kepler-Stern (stella octangula), welcher ebenfalls acht Spitzen hat.

Abb. 12: Stern mit acht Spitzen
Die Abbildung 13 zeigt ein Papiermodell dieses Sterns.

Abb. 13: Papiermodell des Sterns
Die Abbildung 14 zeigt eines der sechs Bauteile des Sterns, die Abbildung 18 im Anhang das zugehrige Schnittmuster.
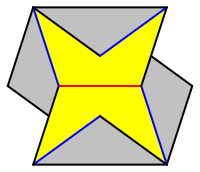
Abb. 14: Bauteil fr den Stern
Das Modell der Abbildung 13 kann ohne Klammern zusammengebaut werden.
7 Link zum Ikosaeder
Die zwlf Endpunkte der eingedrckten Walmdachfirste spannen ein Ikosaeder auf. Die Abbildung 15 zeigt die schematische Darstellung. Die Walmdachfirste sind rot gezeichnet, die Kanten des Ikosaeders orange.

Abb. 15: Ikosaederkanten
In der Abbildung 16 sind die sichtbaren Seitenflchen des Ikosaeders angegeben.
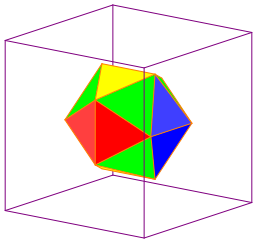
Ikosaeder
8 Anhang: Schnittmuster
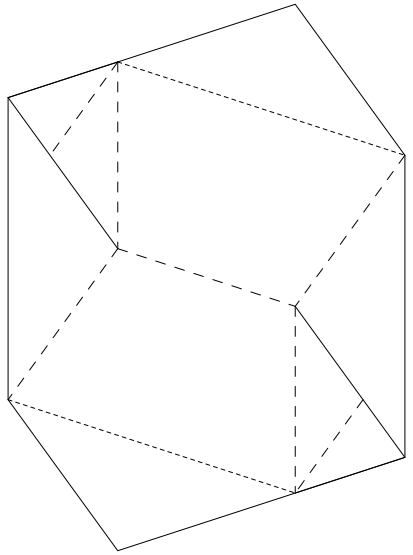
Abb. 17: Schnittmuster fr Dodekaeder-Wrfel
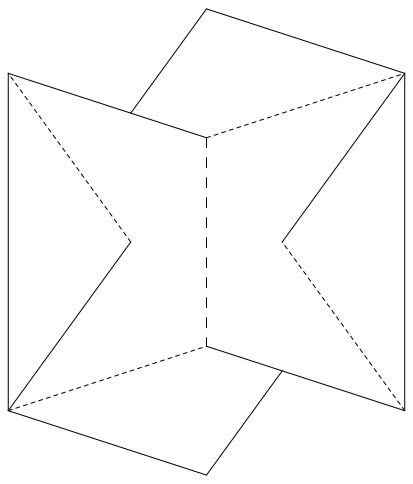
Abb. 18: Schnittmuster fr den Stern