Hans Walser, [20140903]

Dodekaeder

1     Worum geht es?

Es wird eine einparametrige Schar von Dodekaedern vorgestellt, welche das regulŠre Pentagondodekaeder und das Rhombendodekaeder enthŠlt.

2     Drei Rhomben

In einem rŠumlichen kartesischen Koordinatensystem beginnen wir mit drei Rhomben mit den Eckpunkten:

            Roter Rhombus:         (0, 1, 0), (0, 0, t), (0, –1, 0), (0, 0, –t)

            GrŸner Rhombus:      (0, 0, 1), (t, 0, 0), (0, 0, –1), (–t, 0, 0)

            Blauer Rhombus:       (1, 0, 0), (0, t, 0), (–1, 0, 0), (0, –t, 0)

Die Abbildung 1 zeigt die Situation fŸr t = 2.

 

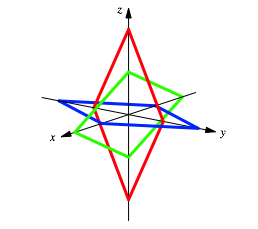
Abb. 1: Drei Rhomben

 

Die drei Rhomben sind topologisch in der Situation von drei borromeischen Ringen (Abb. 2a). Die Abbildung 2b zeigt das Durchdringungsverhalten der drei Rhomben.

 

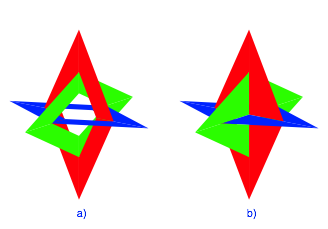
Abb. 2: Borromeische Ringe. Durchdringung

 

3     Drei Prismen

Wir verwenden jeden Rhombus als Leitlinie eines geraden Prismas (Abb. 3).

 

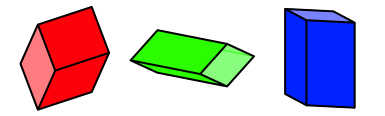
Abb. 3: Drei Prismen

 

Die Abbildung 4 zeigt je zwei der drei Prismen.

 

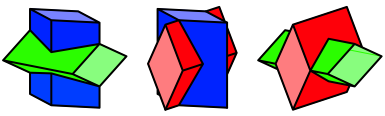
Abb. 4: Paare von Prismen

 

4     Oktaeder

Die Abbildung 5 zeigt die Schnittfiguren der Prismenpaare der Abbildung 4.

 

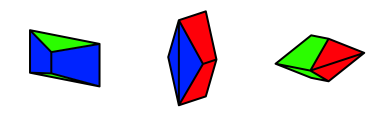
Abb. 5: Schnittfiguren

 

Die Schnittfiguren haben je acht SeitenflŠchen, sind also Oktaeder. Je vier SeitenflŠchen sind kongruente Dreiecke oder kongruente gleichschenklige Trapeze.

5     Dodekaeder

Die Schnittfigur aller drei Prismen gibt ein Dodekaeder (Abb. 6).

 

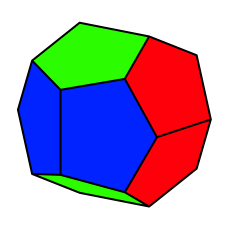
Abb. 6: Dodekaeder

 

Das Dodekaeder besteht in der Regel (eine Ausnahme werden wir gleich kennen lernen) aus zwšlf kongruenten, aber nicht regelmŠ§igen FŸnfecken. Die FŸnfecke sind achsensymmetrisch. Vier der fŸnf Kanten sind gleich lang. Die fŸnfte Kante (ãBasisÒ) hat eine abweichende LŠnge. An einer Basis sto§en jeweils gleichfarbene FŸnfecke zusammen.

Der Winkel α zwischen zwei an einer Basis zusammensto§enden FŸnfecken betrŠgt:

α = 2arctan(t)

Im gezeichneten Sonderfall mit t = 2 ist also α = 2arctan(2) Å 126.87¡.

6     SonderfŠlle

6.1    Rhombendodekaeder

FŸr t = 1 ergibt sich das Rhombendodekaeder. Die Basis der FŸnfecke schrumpft zu einem Punkt, so dass Rhomben Ÿbrig bleiben.

6.2    RegulŠres Pentagondodekaeder

FŸr  (Goldener Schnitt) ergibt sich das regelmŠ§ige Pentagondodekaeder.