Hans Walser, [20180115]

Doppelpyramide im Würfel

1 Worum geht es?

Eine Sechskant-Doppelpyramide im Würfel steht sowohl volumenmäßig wie auch oberflächenmäßig im selben rationalen Verhältnis zu den entsprechenden Würfeldaten.

2 Kürzeste Wege auf der Würfeloberfläche

Die Abbildung 1a zeigt die sechs kürzesten Wege welche auf der Würfeloberfläche zwei diametrale Eckpunkte verbinden. Die sechs Übergangspunkte über die Würfelkanten bilden ein regelmäßiges Sechseck (Abb. 1b).

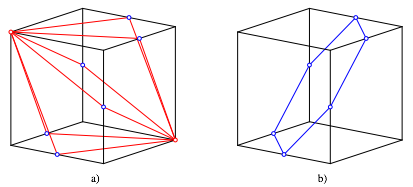
Abb. 1: Kürzeste Wege

Wir ergänzen zu einer Sechskant-Doppelpyramide (Abb. 2).

Sämtliche Kanten dieser Pyramide liegen auf der Würfeloberfläche. Beim Einheitswürfel haben die roten Schrägkanten die Länge . Die blauen Sechseckseiten haben die Länge .

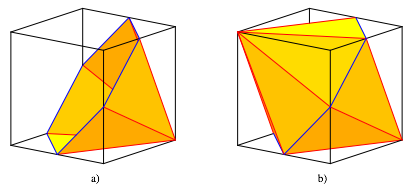
Abb. 2: Sechskant-Doppelpyramide

3 Volumen und Oberfläche

Obwohl die Längen der Pyramidenkanten und der Sechseckseiten irrationale Zahlen sind, ergeben sich „schöne“ Werte für Volumen und Oberfläche der Doppelpyramide.

3.1 Volumen

Für die Grundfläche (Sechseckfläche) G erhalten wir:

(1)

Jede der beiden Teilpyramiden hat die Höhe . Somit erhalten wir für das Volumen V der Doppelpyramide:

(2)

Das Volumen der Doppelpyramide ist drei Viertel des Würfelvolumens.

3.2 Oberfläche

3.2.1 Rechnerisches Vorgehen

Die Oberfläche der Doppelpyramide besteht aus zwölf gleichschenkligen Dreiecken der Schenkellänge und der Basislänge . Ein einzelnes Dreieck hat somit die Höhe :

(3)

Daraus erhalten wir die gesamte Oberfläche S:

(4)

Der Würfel hat die Oberfläche 6. Die Doppelkegeloberfläche ist also drei Viertel der Würfeloberfläche.

Wir haben sowohl beim Volumen wie bei der Oberfläche im Vergleich zum Würfel den Faktor drei Viertel.

3.2.2 Visuelles Vorgehen

Jedes zweite gleichschenklige Dreieck der Doppelpyramide liegt in einer Würfelseite gemäß Abbildung 3.

Abb. 3: Dreieck im Quadrat

Da sieht man sofort, dass die weiße Ergänzungsfläche im Quadrat ausmacht. Die Dreiecksfläche misst also der Quadratfläche. Der Rest ist Rechnung.