Hans Walser, [20080910a]
Doppelter Schnittpunkt
1
Der Schnittpunkt
Wir beginnen mit einem
Sehnensechseck 
mit der
Eigenschaft, dass die an einer Ecke 
ansto§enden
Seiten jeweils gleich lang sind, also:
Dann haben die drei
Geraden 
, einen gemeinsamen Schnittpunkt P (Abb. 1).
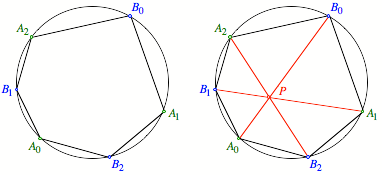
Abb. 1 Sechseck und
Schnittpunkt
Dieser Schnittpunkt P kann auf zwei Arten als ãbesonderer PunktÒ gesehen
werden.
2
Inkreismittelpunkt
Im Dreieck 
ist der Punkt P der Schnittpunkt der Winkelhalbierenden, also der Inkreismittelpunkt (Abb. 2).
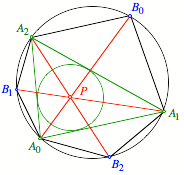
Abb. 2
Inkreismittelpunkt
Die Winkel 
und 
sind nŠmlich Peripheriewinkel
Ÿber gleich langen Sehnen und daher gleich gro§. Die Gerade 
halbiert also
den Dreieckswinkel bei 
. Entsprechendes gilt fŸr die beiden anderen Geraden.
Damit ist auch
bewiesen, dass die drei Geraden 
, tatsŠchlich kopunktal sind.
3
Hšhenschnittpunkt
Die Abbildung 3 lŠsst
vermuten, dass der Schnittpunkt P der Hšhenschnittpunkt im Dreieck 
ist.
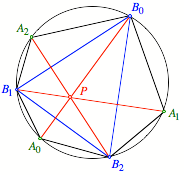
Abb. 3 Hšhenschnittpunkt
Dies ist tatsŠchlich
der Fall.
Die Winkel 
und 
sind als
Peripheriewinkel Ÿber gleich langen Sehnen gleich gro§; dasselbe gilt fŸr die
Winkel 
und 
. Die beiden Dreiecke 
und 
sind daher
spiegelbildlich bezŸglich der Seite 
. Somit steht die Gerade 
, also die Gerade 
, senkrecht auf der Seite 
und ist eine
Hšhe des Dreieckes 
. Analog fŸr die beiden anderen Geraden.