Hans Walser, [20210417]
Drachenspirale
Idee und Anregung: G. Sch., Sch.
1 Worum geht es?
Die Drachenkurve hat im Prinzip ein spiralfšrmiges Verhalten. Es handelt sich um eine eckige logarithmische Spirale.
Verallgemeinerung.
2 Die Drachenkurve
Die Abbildung 1 zeigt das Entstehen der klassischen Drachenkurve. Am jeweiligen Endpunkt des Streckenzuges wird eine um 90ˇ im Uhrzeigersinn verdrehte Kopie des bisherigen Streckenzuges angefźgt. Die LŠnge der Streckenzźge verdoppelt sich von Schritt zu Schritt.
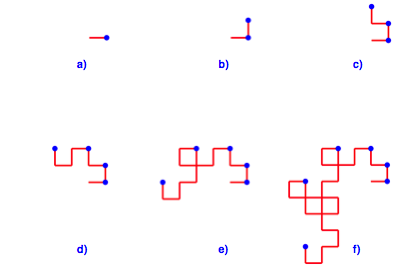
Abb. 1: Genesis der Drachenkurve
Die blauen Abschnittspunkte sind die Ecken einer eckigen logarithmischen Spirale (Abb. 2). Dies wird sofort klar, wenn die grźnen Speichen (Abb. 2b) in den Entstehungsprozess der Drachenkurve mit einbezogen werden. In der Abbildung 2b ist auch die zugehšrige gekrźmmte logarithmische Spirale eingezeichnet.
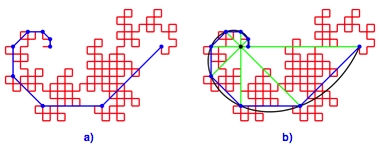
Abb. 2: Logarithmische Spirale
Die Abbildung 3 zeigt ein aus einem lŠngs einer Diagonalen halbierten Origami-Papier hergestelltes Faltmodell derselben eckigen Spirale.

Abb. 3: Faltmodell
Die Abbildung 4 zeigt ein deftigeres Beispiel.
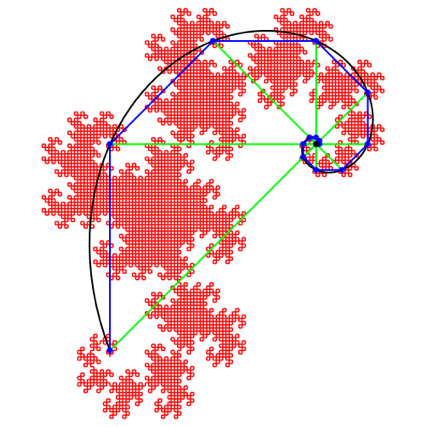
Abb. 4: LŠngere Kurve
3 Verallgemeinerung
Im Beispiel der Abbildungen 1, 2 und 4 wurde jeweils um 90ˇ im Uhrzeigersinn gedreht. Im Folgenden einige Beispiele mit anderen Drehwinkeln. Bei Drehwinkeln grš§er als 60ˇ verlŠuft die Spirale auswŠrts, das hei§t der Radialabstand wŠchst monoton mit dem positiven Drehsinn. Beim Drehwinkel 60ˇ wird die Spirale zu einem Kreis. Bei Drehwinkeln kleiner als 60ˇ verlŠuft die Spirale einwŠrts.
3.1 Drehwinkel 120ˇ
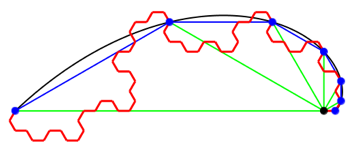
Abb. 5.1: Drehwinkel 120ˇ
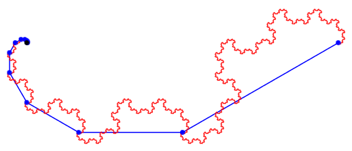
Abb. 5.2: Drehwinkel 120ˇ
3.2 Drehwinkel 108ˇ
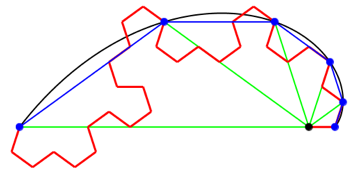
Abb. 6.1: Drehwinkel 108ˇ
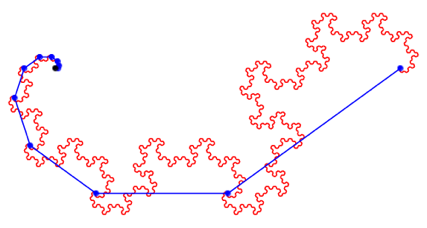
Abb. 6.2: Drehwinkel 108ˇ
3.3 Drehwinkel 93ˇ
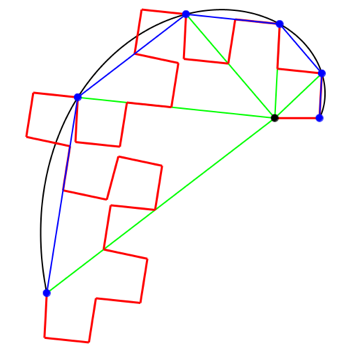
Abb. 7.1: Drehwinkel 93ˇ
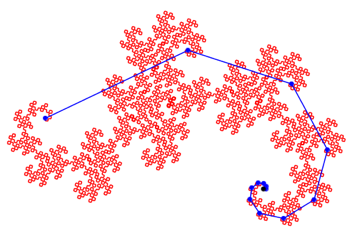
Abb. 7.2: Drehwinkel 93ˇ
3.4 Drehwinkel 87ˇ
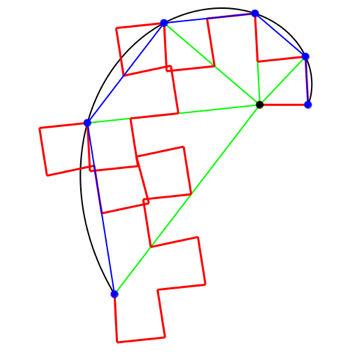
Abb. 8.1: Drehwinkel 87ˇ
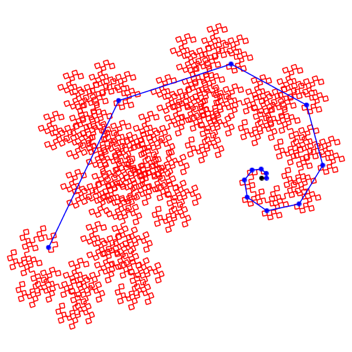
Abb. 8.1: Drehwinkel 87ˇ
3.5 Drehwinkel 72ˇ
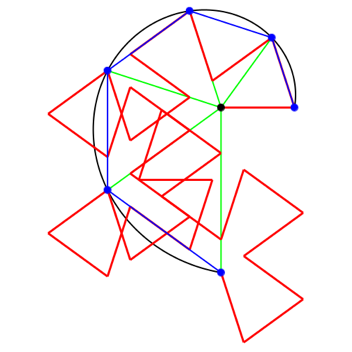
Abb. 9.1: Drehwinkel 72ˇ
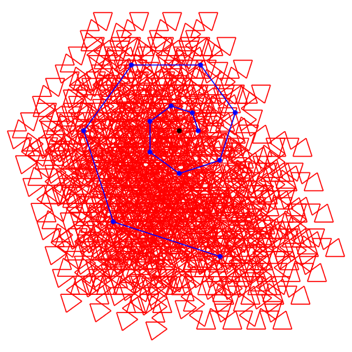
Abb. 9.2: Drehwinkel 72ˇ
3.6 Drehwinkel 60ˇ
Beim Drehwinkel 60ˇ wird die Spirale zum Kreis.
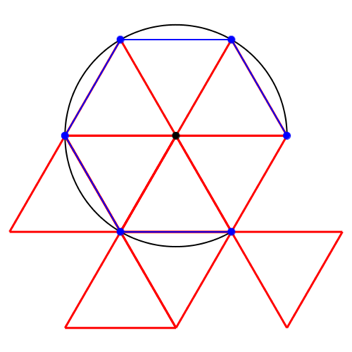
Abb. 10.1: Drehwinkel 60ˇ
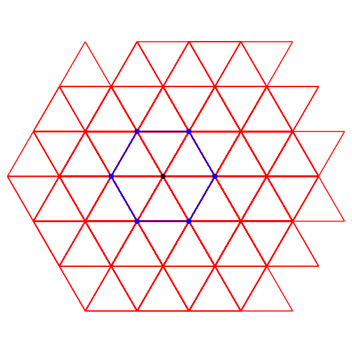
Abb. 10.2: Drehwinkel 60ˇ
3.7 Drehwinkel 45ˇ
Bei Drehwinkeln kleiner als 60ˇ verlŠuft die Spirale einwŠrts.
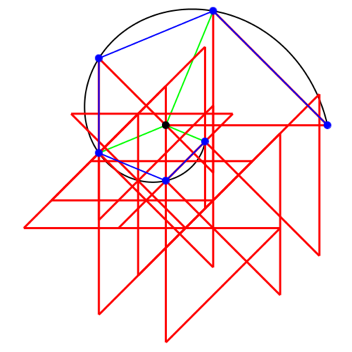
Abb. 11.1: Drehwinkel 45ˇ
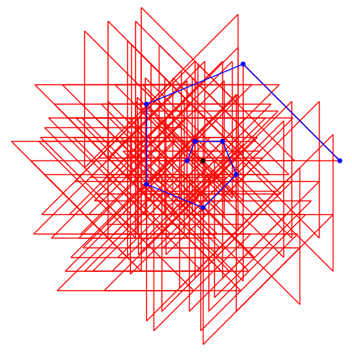
Abb. 11.2: Drehwinkel 45ˇ
4 Animationen
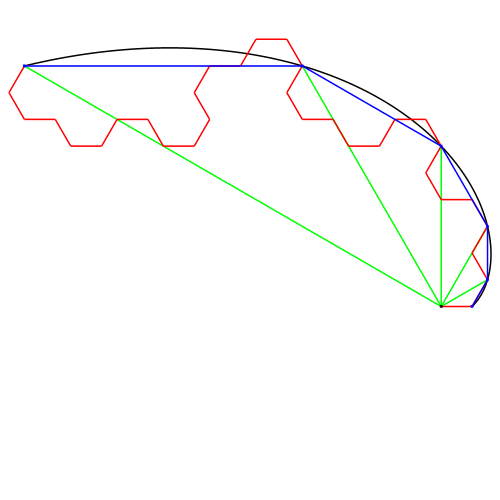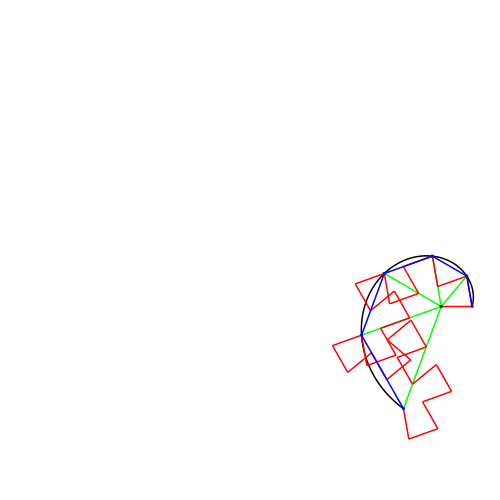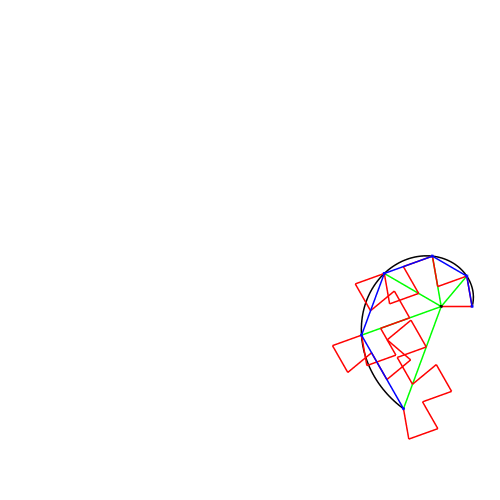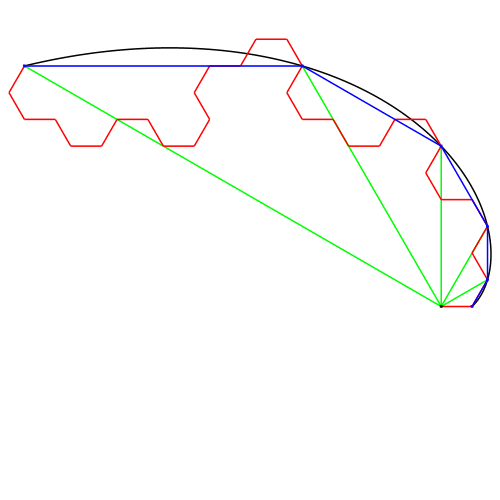
Abb. 12: Animation

Abb. 13: Animation