Hans Walser, [20200120]
Drehpunkt
1 Problemstellung
Zwei rechtwinklige Dreiecke ABC und ABD mit den rechten Winkeln in C beziehungsweise D haben die Ecken A und B gemeinsam (Abb. 1). Die Ecken C und D liegen auf dem gemeinsamen Thaleskreis.
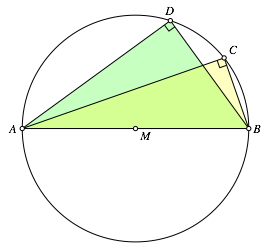
Abb. 1: Zwei rechtwinklige Dreiecke
Gesucht ist die Drehung (Drehpunkt und Drehwinkel), welche den rechten Winkel bei C auf den rechten Winkel bei D abbildet.
Eine Fallensteller-Aufgabe.
2 Falsche Lšsung
Wir drehen C um den Mittelpunkt M des Thaleskreises nach D.
Die Abbildung 2 zeigt, was dann mit dem Dreieck ABC passiert.
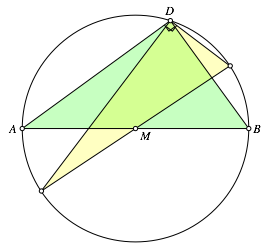
Abb. 2: Drehung um den Mittelpunkt des Thaleskreises
Es werden nur die Ecken beim rechten Winkel aufeinander abgebildet, nicht aber die rechten Winkel.
3 Schrittweises Vorgehen
Da der Punkt C auf den Punkt D gedreht werden muss, ist der Drehpunkt auf der Mittelsenkrechten der Strecke CD.
Diese schneide den Thaleskreis in den Punkten P und Q (Abb. 3).
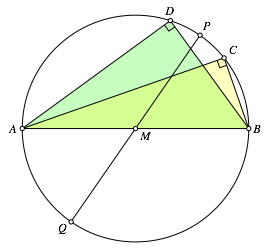
Abb. 3: Mittelsenkrechte
Die Punkte AQBP bilden ein Rechteck (Abb. 4).
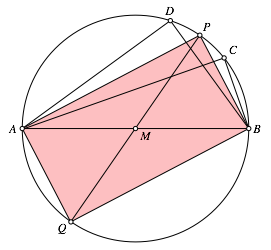
Abb. 4: Rechteck
Der Punkt P liegt in der Mitte des Bogens CD. Daher ist die Gerade AP die eine Winkelhalbierende der Geraden AC und AD. Die Gerade AQ ist die andere Winkelhalbierende dieser beiden Geraden.
Da diese beiden Geraden durch die gesuchte Drehung aufeinander abgebildet werden mźssen, ist der Drehpunkt auf einer dieser Winkelhalbierenden.
Somit kommen als Drehpunkte nur noch die Punkte P und Q in Frage.
Die Abbildung 5 zeigt die Situation bei einer Drehung um P. Der Drehwinkel ist der Winkel CPD. Man kann diskutieren, ob dies eine zulŠssige Lšsung ist.
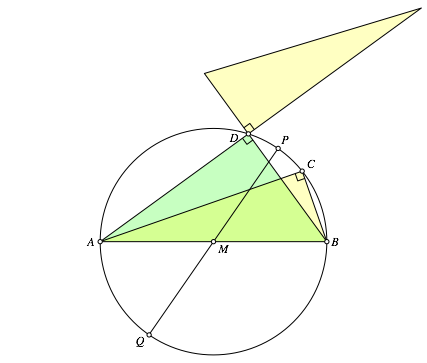
Abb. 5: Drehung um P.
Die Abbildung 6 zeigt die Situation bei einer Drehung um Q. Der Drehwinkel ist der Winkel CQD. ooo
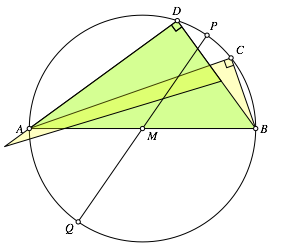
Abb. 6: Drehung um Q.