Hans Walser, [20220118]
Drei Sichten
1 Problemstellung
Gesucht sind Figuren, welche von oben als Kreis, von vorne als Quadrat und von der Seite als ein auf einer Ecke stehendes Quadrat gemäß Abbildung 1 aussehen.
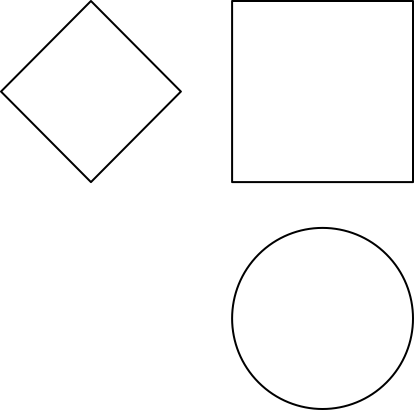
Abb. 1: Drei Sichten
Die Abbildung 2 gibt die genauen Größenverhältnisse der drei Umrisse. Für technische Zwecke und Berechnungen wird der Kreisradius eins gesetzt.
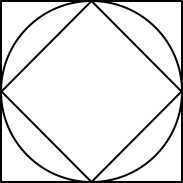
Abb. 2: Größenverhältnisse
2 Einige Lösungen
Da nur drei spezielle Umrisse festgelegt sind, gibt es unendlich viele Lösungen.
Bei den folgenden Beispielen werden die drei speziellen Sichten und eine allgemeine Ansicht gegeben.
2.1 Lösung nach George Polya
Die Lösung kann aus einem runden Besenstiel herausgeschnitten werden.
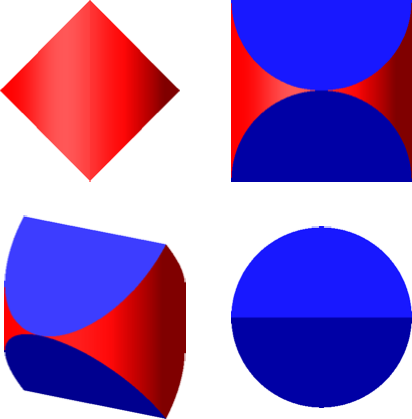
Abb. 3: Lösung nach Polya

Abb. 4: Animation der Lösung von Polya
Für das Volumen V ergibt sich:
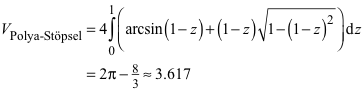 (1)
(1)
Für einen Kreisradius r ergibt sich allgemein:
![]() (2)
(2)
Bei r = 3 also:
![]() (3)
(3)
Für die Oberfläche S ergibt sich:
![]() (4)
(4)
Für einen Kreisradius r ergibt sich allgemein:
![]() (5)
(5)
Bei r = 3 also:
![]() (6)
(6)
2.2 Lösung nach Jürgen Elschenbroich
Diese Lösung wird auch als Konoid bezeichnet. Die horizontalen Schnitte sind Ellipsen mit der langen Halbachse eins und der kurzen Halbachse zwischen null und eins.

Abb. 5: Lösung nach Elschenbroich

Abb. 6: Animation der Lösung Elschenbroich
Das Volumen V des Konoides ist (Herleitung mit dem Prinzip von Cavalieri):
![]() (7)
(7)
Für einen Kreisradius r ergibt sich allgemein:
![]() (8)
(8)
Bei r = 3 also:
![]() (9)
(9)
2.3 Lösung nach Bernd Wollring
Diese Lösung ist die konvexe Hülle des Gerüstes der Abbildungen 9 und 10.
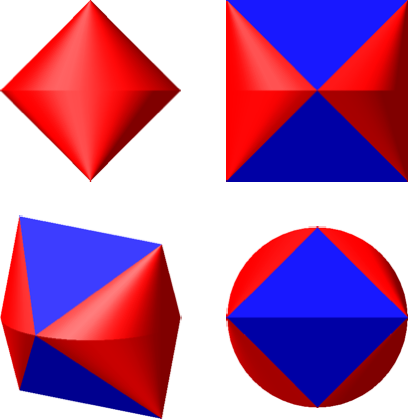
Abb. 7: Lösung nach Wollring

Abb. 8: Animation der Lösung Wollring
Das Volumen V der konvexen Hülle ist (Herleitung mit dem Prinzip von Cavalieri):
![]() (10)
(10)
Für einen Kreisradius r ergibt sich allgemein:
![]() (11)
(11)
Bei r = 3 also:
![]() (12)
(12)
2.4 Gerüst
Das Gerüst hat das Volumen null.
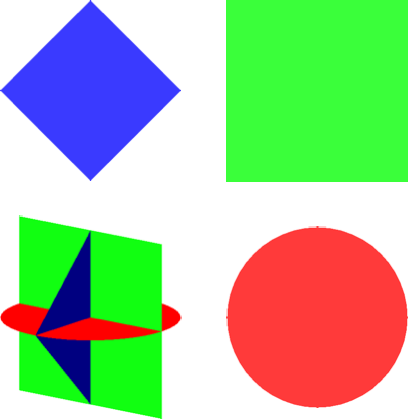
Abb. 9: Gerüst
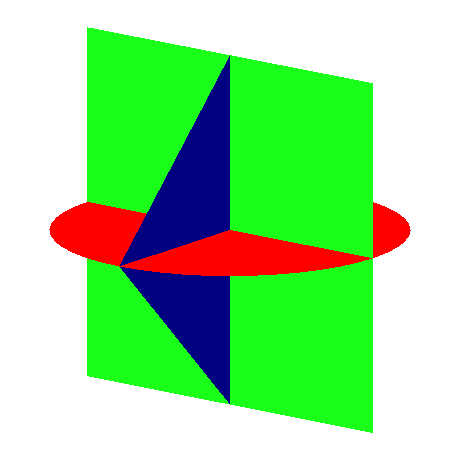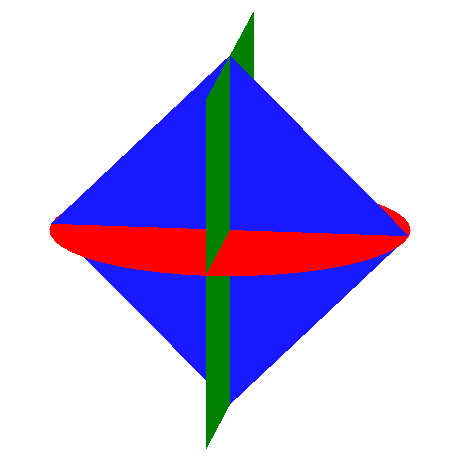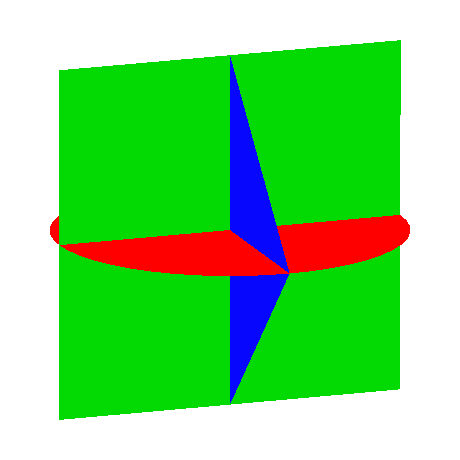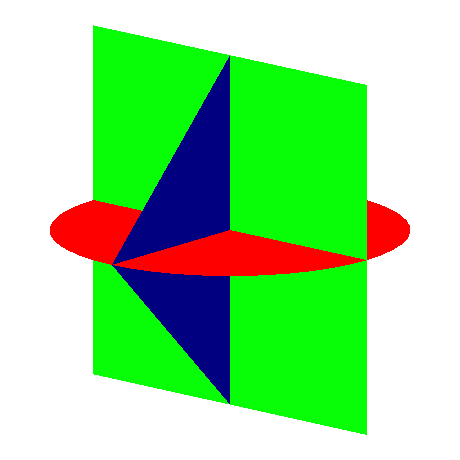
Abb. 10: Animation des Gerüstes
3 Modifikation
Aus bestehenden Lösungen finden wir durch geeignete Modifikationen weitere Lösungen. Zum Beispiel kann man aus der Lösung nach Polya (Abb. 3 und 4) volumenmäßig einen Achtel herausschneiden (Abb. 11 und 12). In den drei speziellen Sichten bleiben die Umrisse erhalten.
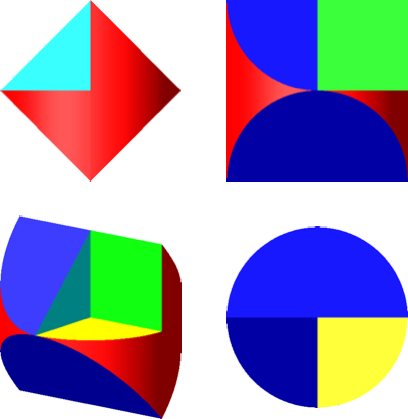
Abb. 11: Modifikation
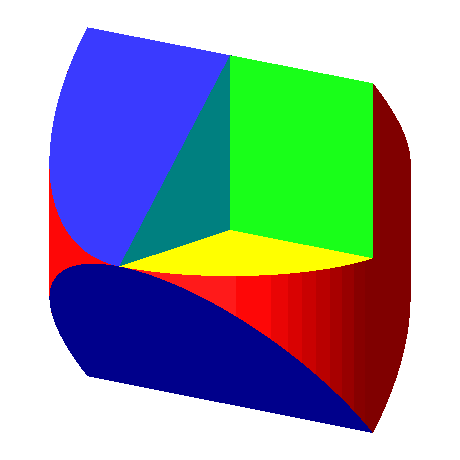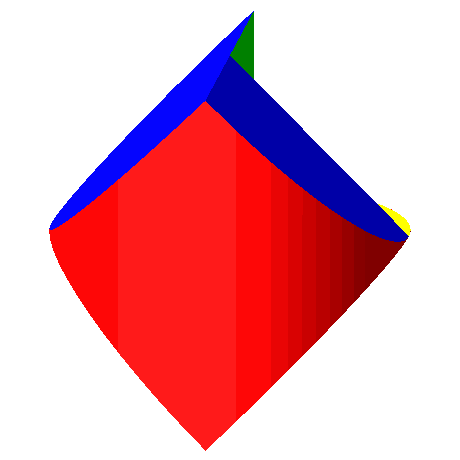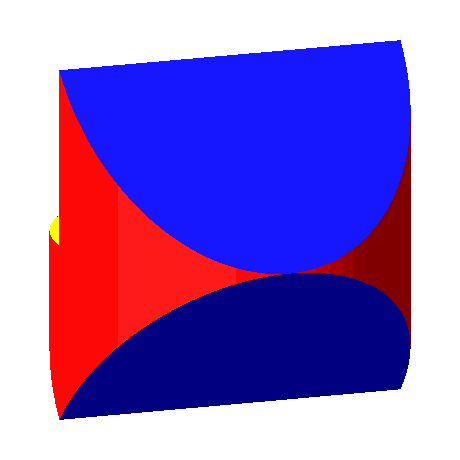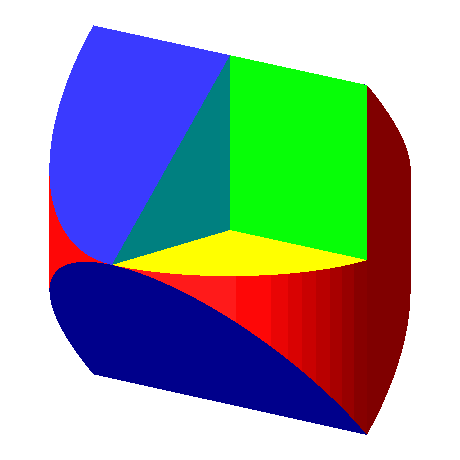
Abb. 12: Animierte Modifikation
4 Vergleich der Volumina
Die Abbildung 13 listet die drei Körper (Lösung nach Polya (Abb. 3 und 4), konvexe Hülle des Gerüstes (Abb. 7 und 8), Konoid (Abb. 5 und 6)) sowie das Gerüst (Abb. 9 und 10) in der Reihenfolge ihrer Volumina auf. Die Lösung nach Polya (Abb. 13 ganz links) hat das größte Volumen nicht nur im Rahmen unserer Beispiele, sondern überhaupt für die Lösung unseres Problems. Das Gerüste (Abb. 13 ganz rechts) hat das Volumen null.
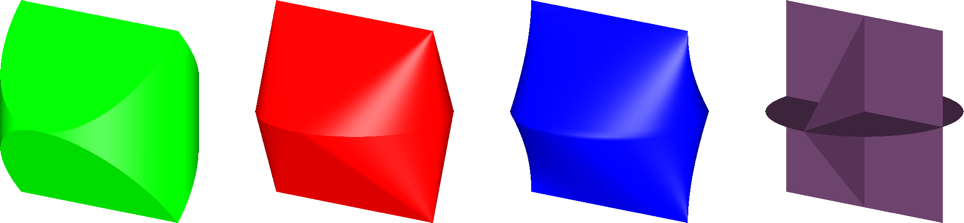
Abb. 13: Die drei Körper und das Gerüst
Wir können das Gerüst in das Konoid, dieses in die konvexe Hülle und diese schließlich in die Lösung nach Polya einpacken. Die Abbildung 14 zeigt die verpackten Figuren. Die ersten beiden Körper haben einen Teil der Oberfläche gemeinsam, wie deutlich sichtbar ist.

Abb. 14: Alles eingepackt
Die folgenden Abbildungen zeigen nun einige Schnitte. Wir sehen, wie die einzelnen Körper und das gemeinsame Gerüst ineinander verpackt sind. Die drei Körper haben die Kanten des Gerüstes gemeinsam. Dies wird jeweils beim Schnitt durch die Mitte sichtbar.
Die Abbildung 15 zeigt horizontale Schnitte. Sie sind parallel zur Kreisscheibe des Gerüstes.
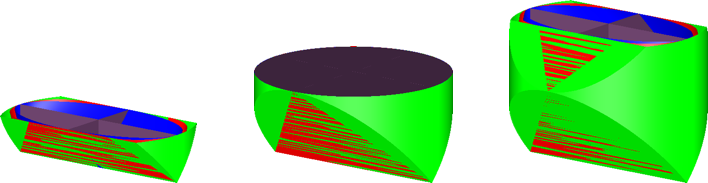
Abb. 15: Horizontale Schnitte
Die Abbildung 16 zeigt den horizontalen Schnitt auf halber Höhe zwischen der Kreisscheibe und der Oberkante.
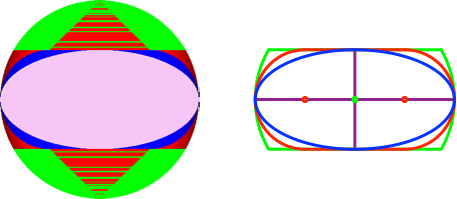
Abb. 16: Schnitt auf halber Höhe zwischen Kreisscheibe und Oberkante
Die Abbildung 17 zeigt die Geometrie der Schnitte einzeln. Die Körper sitzen ineinander drin, haben aber das Gerüst gemeinsam. Da die Flächeninhalte dieser Schnitte leicht zu berechnen sind, lässt sich integrativ auch das Volumen der zugehörigen Körper ermitteln.

Abb. 17: Einzelne Schnitte
Die Abbildung 18 zeigt drei senkrechte Schnitte parallel zum großen Quadrat. Der Autor wüsste gerne, um welche Kurven es sich da handelt.

Abb. 18: Senkrechte Schnitte parallel zum großen Quadrat
Und schließlich (Abb. 19) senkrechte Schnitte parallel zum kleinen Quadrat.

Abb. 19: Senkrechte Schnitte parallel zum kleinen Quadrat
5 Weitere Lösungen
Die Abbildung 20 zeigt eine einparametrige Schar von Lösungen.
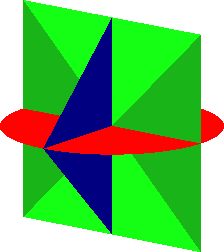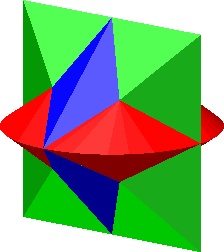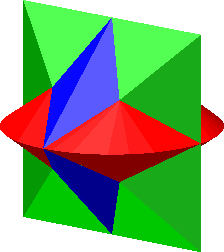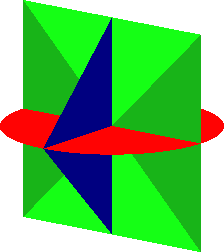
Abb. 20: Lösungsschar
Die Lösungen erscheinen von oben als Kreis (Abb. 21), von vorne als Quadrat (Abb. 22) und von der Seite als ein auf einer Ecke stehendes Quadrat (Abb. 23).

Abb. 21: Sicht von oben

Abb. 22: Sicht von vorne

Abb. 23: Sicht von der Seite
Websites
Hans Walser: Rohrpost
http://www.walser-h-m.ch/hans/Miniaturen/R/Rohrpost/Rohrpost.htm
Hans Walser: Sphäroid
http://www.walser-h-m.ch/hans/Miniaturen/S/Sphaeroid/Sphaeroid.htm
Hans Walser: Paraboloid-Stern
http://www.walser-h-m.ch/hans/Miniaturen/P/Paraboloid-Stern/Paraboloid-Stern.htm
Hans Walser: Pyramidoid
http://www.walser-h-m.ch/hans/Miniaturen/P/Pyramidoid/Pyramidoid.htm
Hans Walser: Dreitafelprojektion
http://www.walser-h-m.ch/hans/Miniaturen/D/Dreitafelprojektion/Dreitafelprojektion.htm