Hans Walser, [20120124], [20201128]
Dreieck dritteln
1 Worum geht es?
Ein beliebiges Dreieck (Abb. 1a) soll flŠchenmŠ§ig gedrittelt werden.
2 Konstruktion
Wir dritteln die Dreiecksseiten (Abb. 1b).
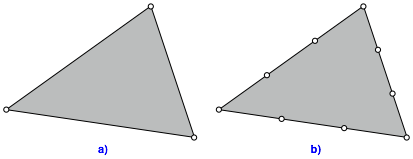
Abb. 1: Dreieckseiten dritteln
Dann verbinden wir gemŠ§ Abbildung 2a oder 2b. Es gibt zwei Lšsungen.
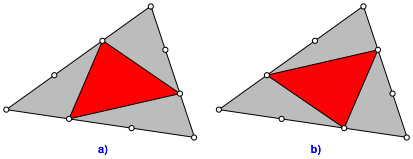
Abb. 2: Das rote Dreieck ist ein Drittel des grauen
Der rechnerische Nachweis sei der Leserin / dem Leser Ÿberlassen oder wer sonst Lust dazu hat. Ist eine Kopfrechnung.
Die beiden Lšsungen sind punktsymmetrisch, also kongruent (Abb. 3). †berlagert bilden sie einen affin verzerrten Davidstern.
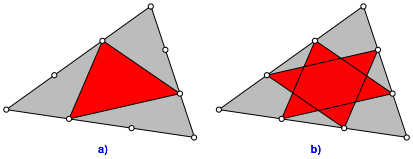
Abb. 3: Kongruente Lšsungen
3 Zerlegungsbeweis
Die Abbildung 4 zeigt einen Zerlegungsbeweis fŸr die Lšsung der Abbildung 2a. Jedes Puzzleteil kommt einmal innen und zweimal au§en vor.
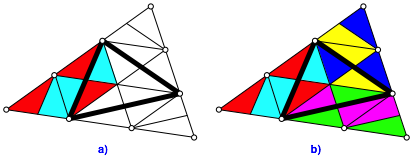
Abb. 4: Zerlegungsbeweis
4 Parkettierung
Die Abbildung 5 zeigt ein Parkett, das aus den beiden Lšsungen zusammengesetzt ist.
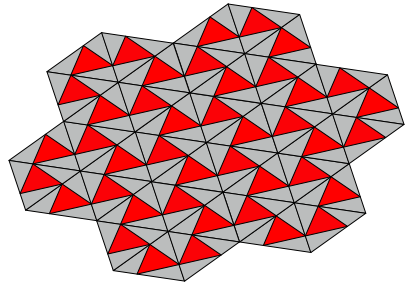
Abb. 5: Parkett
Der rote Anteil ist flŠchenmŠ§ig halb so gro§ wie der sichtbare graue.
5 Iteration und Formen
Das rote Drittel-Dreieck in den Abbildungen 2a und 6a hat nicht dieselbe Form wie das graue Startdreieck.
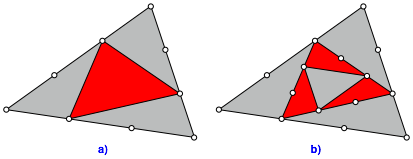
Abb. 6: Iteration und €hnlichkeit
Wenn wir aber den Drittelungsprozess auf das rote Drittel-Dreieck
anwenden, erhalten wir ein Dreieck (gegenŸber dem Startdreieck ist es das
Neuntel-Dreieck), das zum Startdreieck Šhnlich ist. Es entsteht aus dem
Startdreieck durch Streckung vom Schwerpunkt aus mit dem Faktor 
. Da dies ein LŠngenverŠnderungsfaktor ist, ergibt sich der
FlŠchenverŠnderungsfaktor 
.
Die Abbildung 7 zeigt weitere Iterationsschritte.
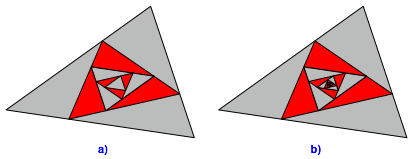
Abb. 7: Weitere Iterationsschritte
6 Beweis
Wir arbeiten mit den Bezeichnungen der Abbildung 8.
ist der
Schwerpunkt des Startdreiecks 
.
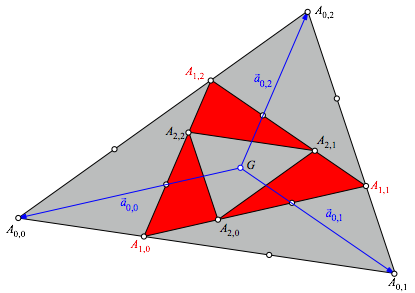
Abb. 8: Bezeichnungen
Weiter sei:
(1)
Da 
der Schwerpunkt
ist, gilt die Schwerpunktbedingung:
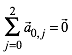(2)
Der Drittelungsprozess lŠsst sich rekursiv wie folgt formulieren:
(3)
FŸr den ersten Schritt bedeutet dies:
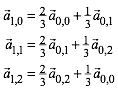(4)
FŸr den zweiten Schritt erhalten wir exemplarisch:
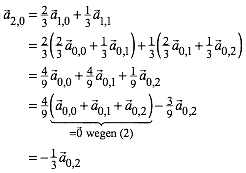(5)
Analog durch zyklische Vertauschung:
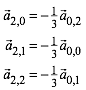(6)
Daraus folgt die Behauptung.