Hans Walser, [20230512]

Dreieck einbeschreiben

1 Problemstellung

Einem Dreieck soll ein Dreieck einbeschrieben werden, dessen Seiten senkrecht auf den Seiten des gegebenen Dreieckes stehen (Abb. 1).

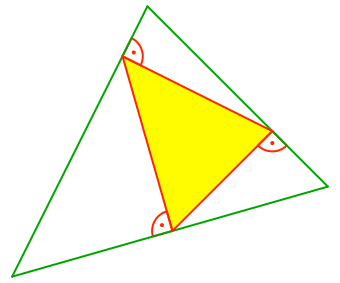
Abb. 1: Dreieck einbeschreiben

2 Lösungswege

2.1 Dynamisch mit falschen Lösungen

Wir wählen einen Startpunkt auf einer Seite (Abb. 2).

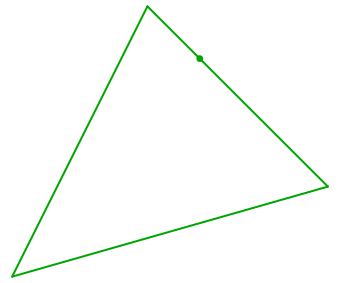
Abb. 2: Startpunkt

Dann loten wir uns durch, bis wir wieder auf die Startseite kommen (Abb. 3).

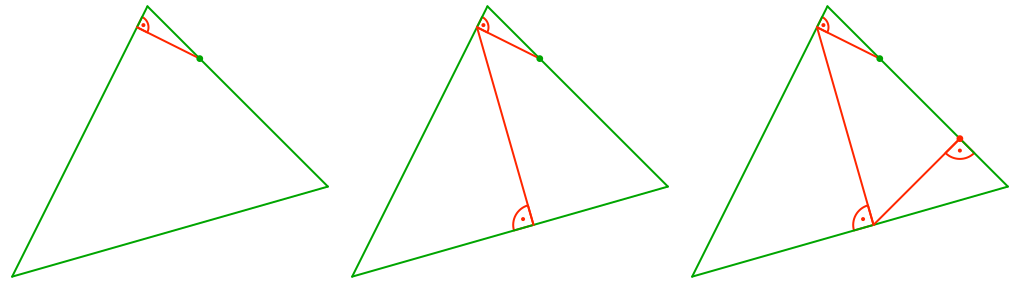
Abb. 3: Durchloten

Wenn der Endpunkt auf den Startpunkt fällt, ist das Problem gelöst. Leider ist das bei uns nicht der Fall. Wir haben eine „falsche Lösung“.

Die Abbildung 4 zeigt, was bei Variation des Startpunktes geschieht.

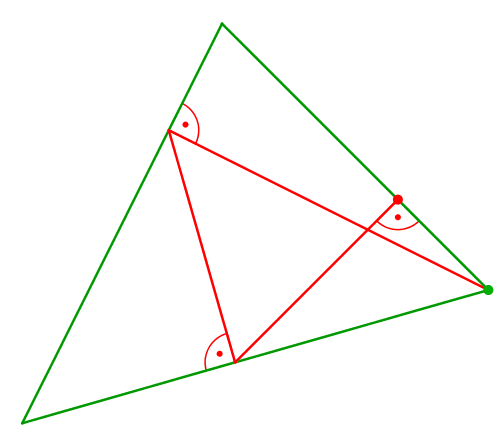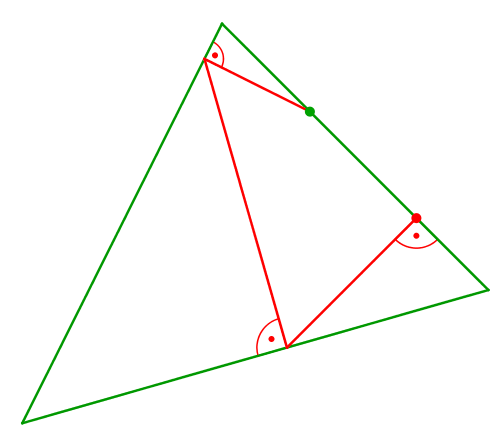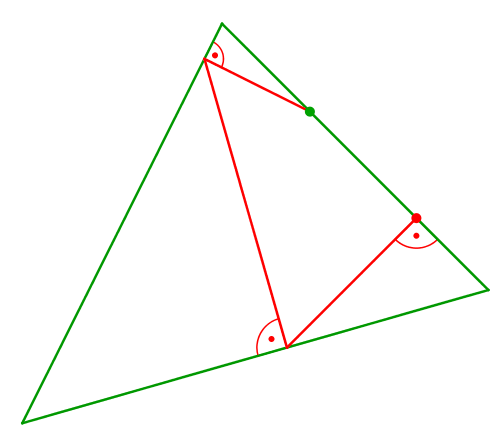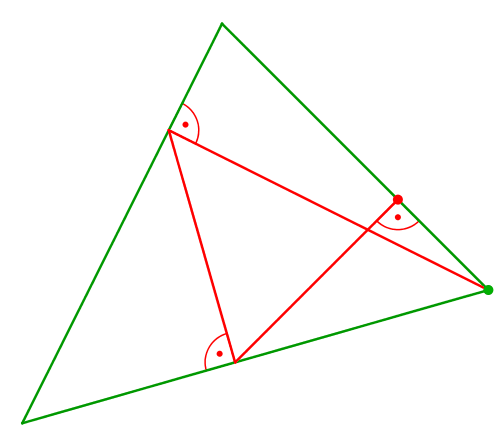
Abb. 4: Variation des Startpunktes

Startpunkt und Endpunkt bewegen sich gegenläufig. Im Treffpunkt ist die Lösung.

Zunächst ist man versucht, wie folgt vorzugehen: Man konstruiert mit einem beliebigen Startpunkt eine falsche Lösung (Abb. 3). Dann nimmt man den Mittelpunkt des Startpunktes und des Endpunktes und startet erneut. Leider funktioniert dies nicht, da sich der Endpunkt viel langsamer bewegt als der Startpunkt.

Der Bremsfaktor ist das Produkt cos(α)•cos(β)•cos(γ), wobei α, β, γ die Winkel des gegebenen Dreieckes sind.

Wir müssen also die Strecke zwischen Startpunkt und Endpunkt einer falschen Lösung im Verhältnis 1 : cos(α)•cos(β)•cos(γ) unterteilen. Der Teilpunkt ist Start- und Endpunkt der richtigen Lösung (Abb. 5).

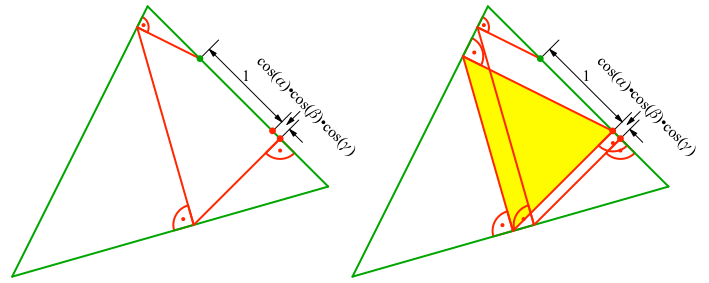
Abb. 5: Unterteilung

Zeichnerisch wird verfahren wie folgt (Abb. 6). Es wird noch ein zweiter Startpunkt durchgeorgelt. Das Verhältnis der Differenzen zwischen den beiden Startpunkten und den zugehörigen Endpunkten ist das gesuchte Teilverhältnis. Die Strahlensätze lassen grüßen.

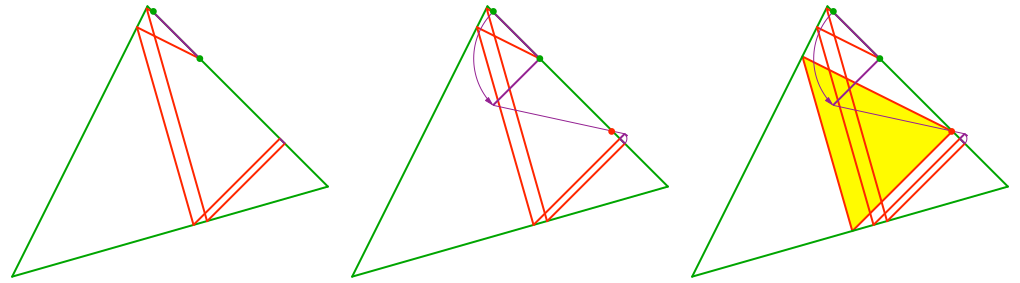
Abb. 6: Zeichnerisches Vorgehen

Bei dieser Methode handelt es sich um die regula falsi, welche seit der Antike von vielen Mathematikern angewendet wurde. Die Idee dabei ist, aus falschen Lösungen Korrekturhinweise zum Auffinden der richtigen Lösung zu gewinnen.

2.2 Dynamisch mit Modelldreieck

Das gesuchte Dreieck ist ähnlich zum gegebenen Dreieck, aber um 90° im Uhrzeigersinn verdreht.

Wir zeichnen nun ein Modelldreieck ein, welches die richtige Form und die richtige Richtung hat, und von dem zwei Ecken auf zwei Seiten des gegebenen Dreieckes liegen (Abb. 7). Es passt alles bis auf die dritte Ecke.

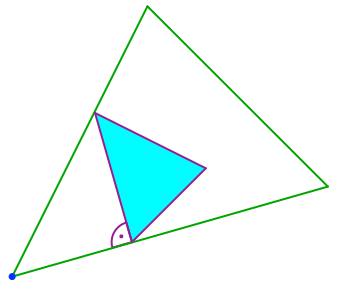
Abb. 7: Modelldreieck

Durch „Aufblasen“ (zentrische Streckung von der blauen Ecke links unten aus) können wir die noch freie Ecke bewegen (Abb. 8). Sie bewegt sich auf einer Geraden.

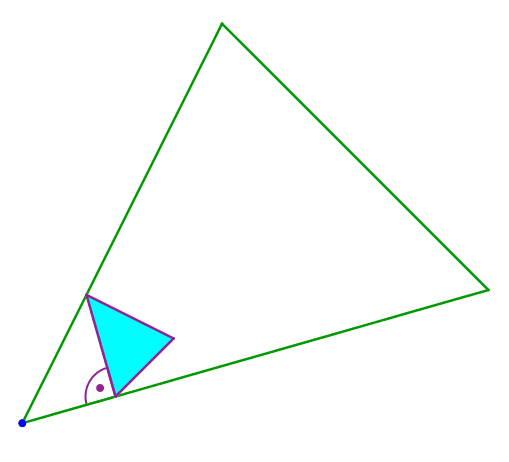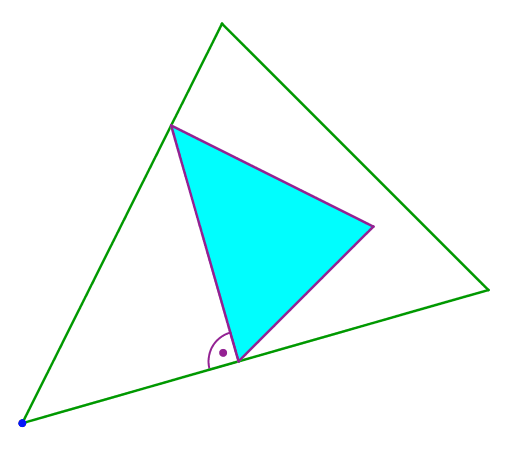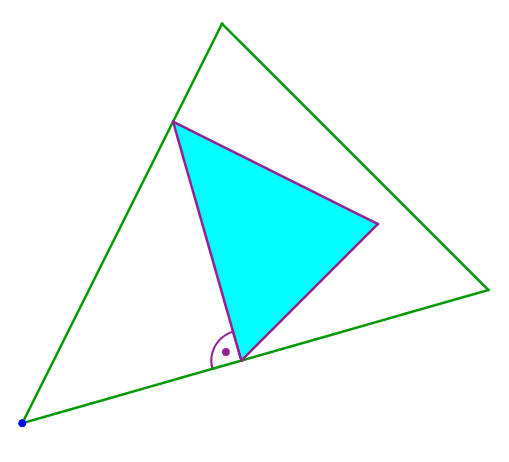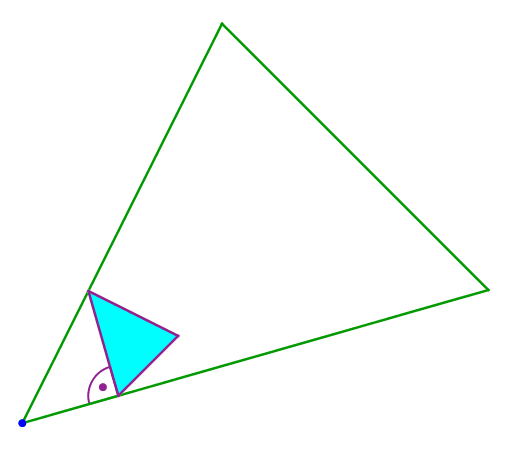
Abb. 8: Aufblasen

Wir schneiden die Gerade, auf der sich die noch freie Ecke bewegt, mit der zugehörigen Dreiecksseite und erhalten so die Lösung (Abb. 9).

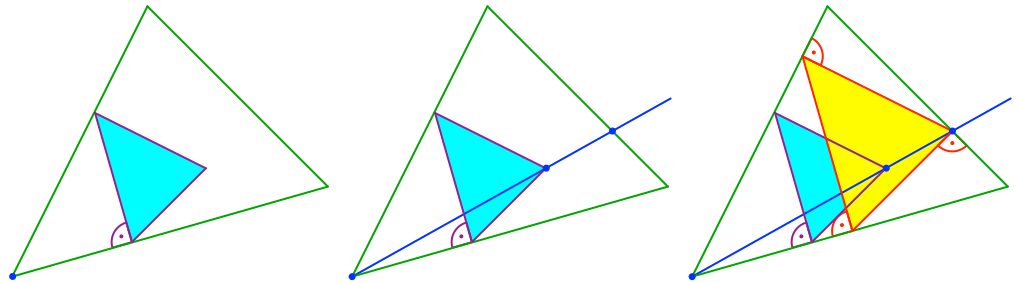
Abb. 9: Strecken bis zum Anschlag

Ein einfach zu konstruierendes Modelldreieck erhalten wir durch Ergänzen einer falschen Lösung zum Dreieck (Abb. 10).

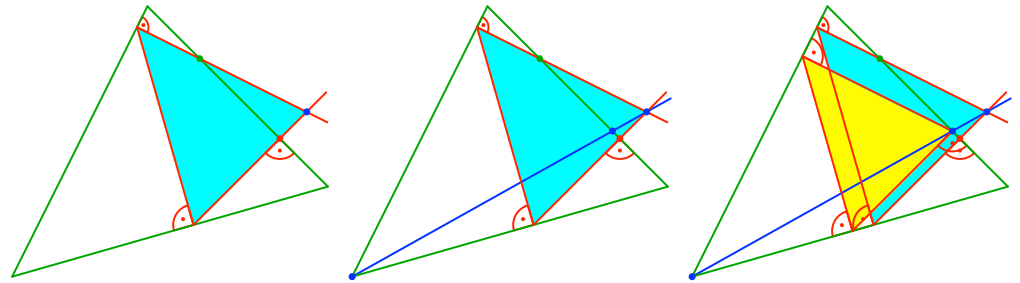
Abb. 10: Einfaches Modelldreieck