Hans Walser, [20100101b]
Dreieck im Raster
1 Worum es geht
Ist das Dreieck ABC gleichseitig?

Gleichseitiges Dreieck?
Leider nein. Fr die
Seitenlngen erhalten wir nmlich:
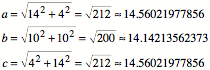
Die Frage ist, ob es in
einem Quadratraster ein gleichseitiges Dreieck geben kann, dessen drei Ecken
Rasterpunkte sind. Auch das geht nicht.
Es kann im
Quadratraster kein gleichseitiges Dreieck geben, dessen drei Ecken Rasterpunkte
sind.
Warum ist das so?
— Beweise folgen.
2
Quadrate im Quadratraster
Zwei Rasterpunkte A und B
lassen sich immer durch Rasterpunkte C und D zu einem in der
Regel ãschrgenÒ Quadrat ergnzen.
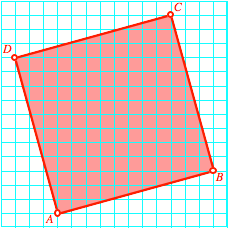
Schrges Quadrat im
Raster
Beweis: Der Vektor ![]() hat ganzzahlige
Komponenten:
hat ganzzahlige
Komponenten:
![]()
Mit dem Vektor ![]() kommen wir von B nach C
und mit dem Vektor
kommen wir von B nach C
und mit dem Vektor ![]() von C nach D.
von C nach D.
Es ist nicht immer
einfach, die ãschrgenÒ Quadrate zu erkennen.
2.1
Wie viele Quadrate sehen wir?
Wie viele Quadrate sind
im Quadratraster erkennbar?
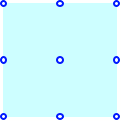
Wie viele Quadrate hat
es im Raster?
Es gibt insgesamt 6
Lsungen:
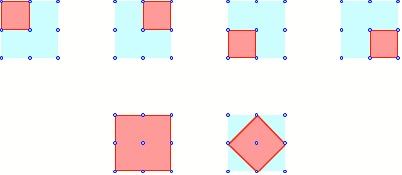
6 Lsungen
2.2
Wie viele Quadrate sehen wir?
Wie viele Quadrate sind
im folgenden Quadratraster erkennbar?
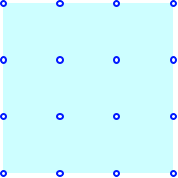
Wie viele Quadrate hat
es im Raster?
Ich komme auf ![]() Lsungen. Die
beiden interessantesten Lsungen sind schrg.
Lsungen. Die
beiden interessantesten Lsungen sind schrg.
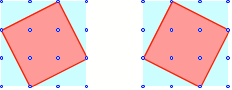
Schrge Lsungen
3
Kein gleichseitiges Dreieck
Wir wollen nun
beweisen, dass es im Quadratraster kein gleichseitiges Rasterdreieck geben
kann.
3.1
Vektorieller Beweis
Wir versuchen, zwei
Rasterpunkte A und B zu einem gleichseitigen Dreieck ABC zu ergnzen.
Der Vektor ![]() hat ganzzahlige
Komponenten:
hat ganzzahlige
Komponenten:
![]()
Der Vektor ![]() ist der um 120¡
gedrehte Vektor
ist der um 120¡
gedrehte Vektor ![]() , also:
, also:
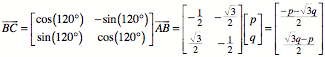
Wegen der
Irrationalitt von ![]() knnen nicht
beide Komponenten von
knnen nicht
beide Komponenten von ![]() ganzzahlig sein.
Der Punkt C ist kein Rasterpunkt.
ganzzahlig sein.
Der Punkt C ist kein Rasterpunkt.
3.2
Beweis mit reductio ad absurdum
Wir nehmen an, es gbe
ein gleichseitiges Rasterdreieck und fhren diese Annahme zu einem Widerspruch.
Zunchst knnen wir das
gleichseitige Rasterdreieck durch Verschieben gem§ den angegebenen
Seitenvektoren zu einem regelm§igen Sechseck ergnzen. Da die Translationsvektoren
gem§ Annahme ganzzahlige Komponenten haben, ist das regelm§ige Sechseck ein
Rastersechseck. Durch Ansetzen von Quadraten erhalten wir schlie§lich ein
regelm§iges Rasterzwlfeck.
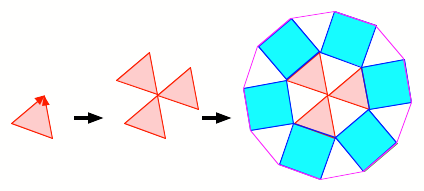
Vom Dreieck zum Zwlfeck
Und nun kommt die eigentliche
reductio ad absurdum: Wir setzen die Seitenvektoren des Zwlfeckes neu in der
Reihenfolge 1, 6, 11, 4, 9, 2, 7, 12, 5, 10, 3, 8 zusammen. Wir nehmen also
jeweils jeden fnften Vektor in zyklischer Reihenfolge. So ergibt sich ein
Stern, dessen zwlf Spitzen ebenfalls Rasterpunkte sind. Diese Spitzen liefern
ein neues regelm§iges Rasterzwlfeck, das viel kleiner ist als das
Ausgangszwlfeck. Der Reduktionsfaktor ist ![]() .
.
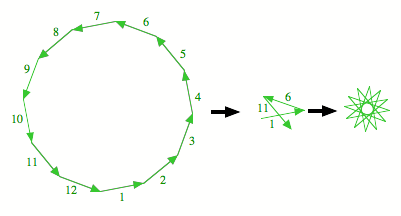
Umbau des Zwlfeckes
Nun knnen wir das
kleine Zwlfeck mit demselben Verfahren wieder um diesen Faktor reduzieren und
erhalten ein noch kleineres. Und so weiter und so fort. Schlie§lich wird das
Zwlfeck so klein, dass es durch die Maschen des Quadratrasters fllt. Dies
steht im Widerspruch dazu, dass die Ecken all dieser Zwlfecke Rasterpunkte
sind. Daher kann das erste Zwlfeck kein Rasterzwlfeck sein, und das Sechseck
kann auch kein Rastersechseck sein und das gleichseitige Dreieck ebenfalls
nicht im Raster liegen.
3.3
Eine logische und eine historische Anmerkung
Wenn wir mit dem
zweiten Beweis, also der reductio ad absurdum, beginnen, knnen wir mit den
Rechnungen des ersten Beweises folgern, dass ![]() eine irrationale
Zahl ist.
eine irrationale
Zahl ist.
Mit demselben Verfahren
der reductio ad absurdum knnen wir zeigen, dass es im Quadratraster kein
regelm§iges Rasterfnfeck geben kann. Daraus wiederum folgt, dass im
regelm§igen Fnfeck das Verhltnis zwischen Seitenlnge und Diagonalenlnge,
also der goldene Schnitt, irrational ist. Dies wurde von Hippasos von Metapont
im 2. Viertel des 5. Jahrhunderts v. Chr. entdeckt. Nun war aber Hippasos
Mitglied der Schule der Pythagoreer, welche die Lehrmeinung vertraten, alles
sei durch Verhltnisse von ganzen Zahlen, also durch rationale Zahlen
darstellbar. Irrationale Zahlen waren in diesem Lehrplan nicht vorgesehen. Die
Legende will, dass Hippasos wegen seiner ketzerischen Entdeckung der
irrationalen Zahlen anlsslich einer Schifffahrt ber Bord gekippt wurde. So
kann es gehen, wenn man den Lehrplan ignoriert.