1 Worum geht es?

Flächensatz am gleichseitigen Dreieck.

2 Konstruktion

In einem gleichseitigen Dreieck zeichnen wir eine zu einer Seite parallele Gerade durch den Schwerpunkt. Auf dieser Geraden wählen wir einen beliebigen Punkt (Abb. 1).

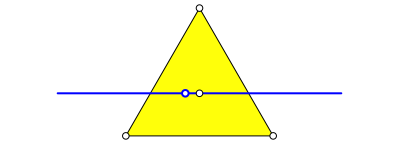
Abb. 1: Disposition

Wir verbinden diesen Punkt mit den Ecken und ergänzen jede Verbindungsstrecke zu einem Quadrat (Abb. 2).

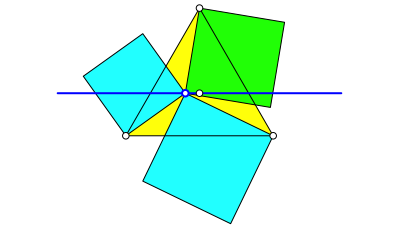
Abb. 2: Quadrate

Wir verdoppeln das grüne Quadrat mit Hilfe einer Diagonalen zu einem roten Quadrat (Abb. 3).

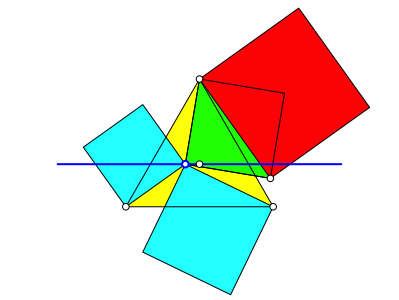
Abb. 3: Verdoppelung zum roten Quadrat

3 Der Flächensatz

In der Situation der Abbildung 3 ist das rote Quadratfläche gleich der Summe der beiden blauen Quadratflächen. Erinnert an den Satz des Pythagoras.

4 Beweis

Wir verwenden die Bezeichnungen und Maße der Abbildung 4. Das gleichseitige Dreieck hat die Seitenlänge 2. Das Dreieck hat damit die Höhe .

Mit t bezeichnen wir die Auslenkung des gewählten Punktes vom Schwerpunkt aus. Weiter sind a, b und d die Verbindungsstrecken zu den Dreiecksecken.

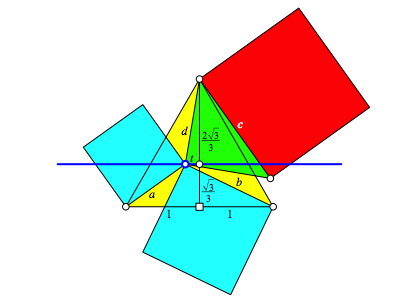
Abb. 4: Maße und Bezeichnungen

Mit Pythagoras finden wir:

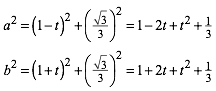(1)

Somit ist:

(2)

Dies ist die Flächensumme der beiden blauen Quadrate.

Weiter ist:

(3)

Dies ist der Flächeninhalt des grünen Quadrates. Das rote Quadrat ist flächenmäßig doppelt so groß. Aus (2) folgt daher die Behauptung.

Bemerkung: Der Sachverhalt ergibt sich als Nebenresultat von [1].

Websites

[1] Hans Walser: Kreisscharen

http://www.walser-h-m.ch/hans/Miniaturen/K/Kreisscharen2/Kreisscharen2.htm