1 Worum geht es?

Experimentelle Kombinatorik. Fleißige Spielerei. Mustererkennung. Fragen der systematischen Darstellung. Winkelüberlegungen.

2 Problemstellung

Wir zeichnen ein regelmäßiges Siebeneck mit allen Diagonalen (Abb. 1).

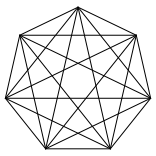
Abb. 1: Siebeneck mit Diagonalen

Die Frage ist nun, wie viele Dreiecke in dieser Figur erkennbar sind.

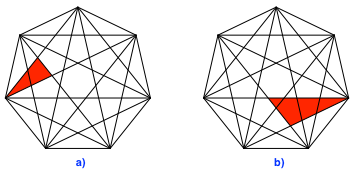
Abb. 2: Beispiele

Es gibt gleichschenklige (Abb. 2a) und ungleichseitige (Abb. 2b) Beispiele. Zu jedem Beispiel ergeben sich durch Siebteldrehungen sechs weitere Beispiele.

3 Auflistung

Wir zeichnen das regelmäßige Siebeneck mit einer senkrechten Symmetrieachse.

3.1 Gleichschenklige Dreiecke

Wir verwenden nun eine standardisierte Darstellung mit senkrechten Symmetrieachsen der gleichschenkligen Dreiecke (Abb. 3 und 4).

3.1.1 Gleiche Symmetrieachse wie das Siebeneck

Die senkrechte Symmetrieachse des Siebeneckes und die Symmetrieachse des gleichschenkligen Dreieckes fallen aufeinander.

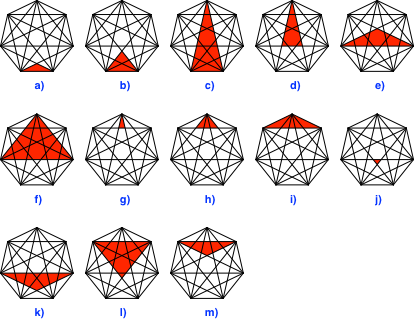
Abb. 3: Gleiche Symmetrieachse

Die Winkel an der Spitze der gleichschenkligen Dreiecke sind ein Siebtel, drei Siebtel oder fünf Siebtel von 180°.

3.1.2 Desaxierte Symmetrieachsen

Die senkrechte Symmetrieachse des Siebenecks und die Symmetrieachse des gleichschenkligen Dreiecks sind parallel, aber verschieden.

Die Dreiecke treten paarweise in spiegelbildlichen Positionen relativ zur senkrechten Symmetrieachse des Siebeneckes auf.

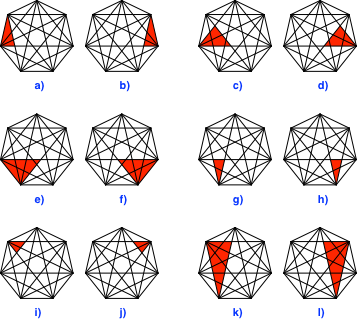
Abb. 4: Desaxierte Symmetrieachsen

Die gleichschenkligen Dreiecke haben dieselbe Form wie jene der Abbildung 3.

3.2 Ungleichseitige Dreiecke

Wir verwenden eine standardisierte Darstellung so, dass die kürzeste Dreieckseite jeweils horizontal liegt (Abb. 5).

Die auftretenden ungleichseitigen Dreiecke sind alle ähnlich. Die drei Winkel dieser Dreiecke sind ein Siebtel, zwei Siebtel und vier Siebtel von 180°.

Die Dreiecke treten paarweise in spiegelbildlichen Positionen auf.

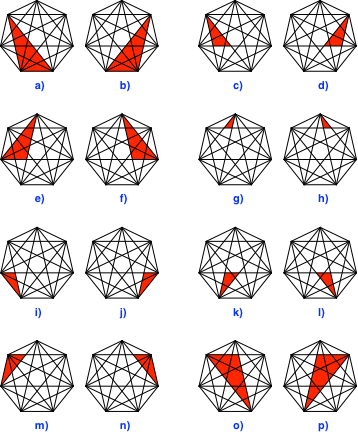
Abb. 5: Ungleichseitige Dreiecke

4 Zusammenfassung

In der standardisierten Darstellung gibt es 13 + 12 + 16 = 41 Dreiecke. Durch Siebteldrehungen ergeben sich insgesamt 287 Dreiecke.

Wir haben insgesamt aber nur vier Formen für die Dreiecke. Drei davon sind gleichschenklig.

Der Autor hofft, dass er nichts übersehen hat.